Одно из практических применений леммы 1

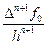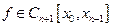Согласно этой лемме величину (если ) можно считать производной 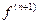(х) в некоторой точке .

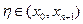Поэтому при малых 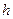число 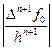может быть использовано в оценках погрешности интерполяции.

Разделенные разности. Пусть теперь 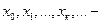произвольные точки оси .

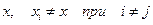Сами значения функции 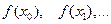функции в узлах называются разделенными разностями нулевого порядка.

Разделенной разностью первого порядка ф-ции 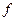(x) называется число

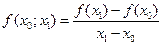. (9.7)

Разделенной разностью второго порядка ф-ции называется число

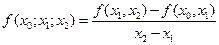. (9.8)

Разделенная разность n-го порядка определяется по рекуррентной формуле через разделенные разности 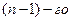порядка:

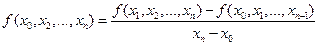. (9.9)

При вычислениях разделенные разности записывают в таблицу

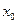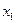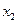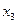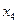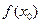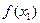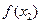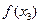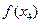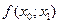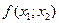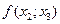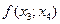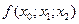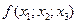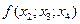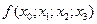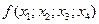Лемма 2. Разделенная разность 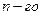порядка выражается через узловые значения функции по формуле

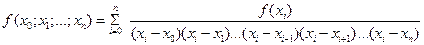, (9.10)

т.е. является симметрической функцией своих аргументов.

Для .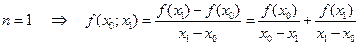

Пусть .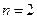

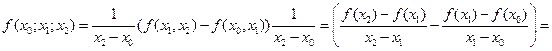
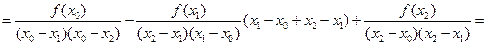
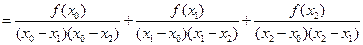. (9.11)

Доказательство для 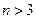производится по индукции.

Из приведенных формул очевидно, что значение разделенной разности 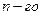порядка не зависит от нумерации 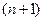узлов, по которым она строится. Поэтому имеется 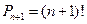возможных вариантов нумерации узлов числами от 0 до .

Лемма 3. Если 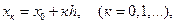т.е. узлы расположены с постоянным шагом 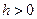, то между разделенной разностью 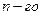порядка и конечной разностью 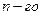порядка имеется следующая связь:

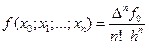. (9.12)

Доказательство. Для 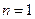равенство (9.12) вытекает из определения разделенной разности

.

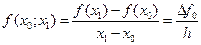При n = 2

.

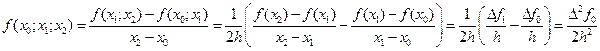При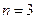

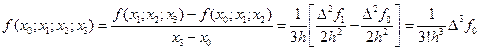, и т.д. для .

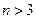Лемма 4. Пусть 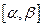- минимальный отрезок, содержащий узлы 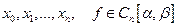. Тогда существует такая точка 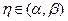, что

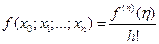. (9.13).

Доказательство леммы в общем случае опускаем.

Следствие леммы 4. Разделенная разность 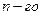порядка от алгебраического многочлена 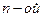степени принимает постоянное значение, не зависящее от выбора узлов 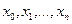, а разделенные разности более высоких порядков равны нулю.

10.Интерполяционный многочлен Ньютона.

Пусть 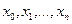- произвольные несовпадающие узлы, в которых известны значения функции .

Лемма 1. Алгебраический многочлен 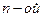степени

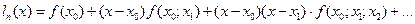
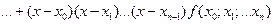(10.1)

является интерполяционным, т.е.

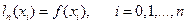. (10.2)

Эти равенства доказываются для произвольных 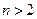по индукции. Для 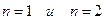можно доказать, воспользовавшись предыдущими формулами.

В некоторых источниках интерполяционный многочлен (10.1) дают в следующей форме:

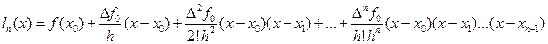, (10.3)

что одно и то же в силу леммы 3 предыдущего параграфа.

Замечание. Многочлен (10.1) называется интерполяционным многочленом Ньютона для неравных промежутков.

Согласно теореме о существовании единственного интерполяционного многочлена 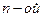степени, удовлетворяющего условиям 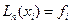, многочлен (10.1) тождественно совпадает с интерполяционным многочленом Лагранжа, т.е. 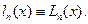Поэтому остаточный член интерполяционного многочлена Ньютона тот же, что и у интерполяционного многочлена Лагранжа, т.е. справедливы следующие cоотношения:

;

;

;

.

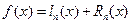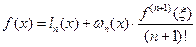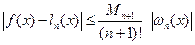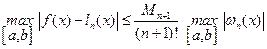При использовании интерполяционного многочлена Лагранжа изменение количества узлов интерполяции требует построения нового многочлена.

Интерполяционный многочлен Ньютона выражается не через значения функции , а через ее разделенные разности. При изменении степени у интерполяционного многочлена Ньютона требуется только добавить или отбросить соответствующее число стандартных слагаемых. Это удобно на практике.