Погрешность линейной интерполяции

В случае линейной интерполяции .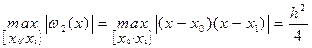

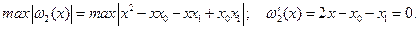
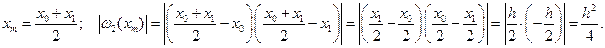
Тогда оценка максимальной погрешности линейной интерполяции на отрезке 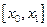в соответствии с (6.29) имеет вид

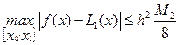, (6.32)

где .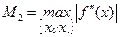

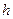Часто задают таблицу большого числа значений некоторой функции с постоянным шагом изменения аргумента.

Тогда при заданном выбираются два ближайших к нему узла. Левый узел принимается за 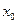, а правый - за 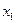, и осуществляется линейная интерполяция по формуле (6.31). Погрешность интерполяции оценивается по формуле (6.32).

Пример. Задана таблица функции 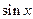с шагом 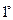. Требуется оценить погрешность линейной интерполяции.

Решение.Шаг 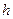таблицы составляет в радианной мере .

.

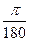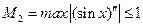Тогда, согласно (6.32),

.

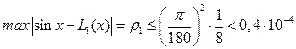Значение 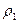оценивалась в предположении, что табличные значения даны точно и вычисления по используемой формуле проведены без погрешностей.

Пусть теперь мы знаем, что предельная абсолютная погрешность округленных табличных значений есть 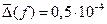. При вычислениях по формуле (6.31) в значении 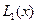возникает погрешность, оцениваемая величиной

.

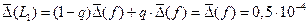После округления значения интерполяционного многочлена с четырьмя десятичными знаками после запятой возникает еще дополнительная погрешность, ограниченная по модулю величиной .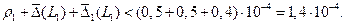

Минимизация погрешности интерполяции.

Многочлены Чебышева.

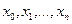Возникает естественный вопрос, как выбрать на отрезке узлы интерполяционного многочлена (6.18)

,

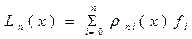чтобы максимальная погрешность интерполяционной функции на этом отрезке была минимальной.

Это очень сложная задача, и решается она для немногих частных функций . Но частично погрешность приближения может быть уменьшена за счет уменьшения .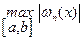

Достигается это нахождением соответствующего расположения узлов интерполяции на отрезке . Одним из таких способов является использование многочленов Чебышева.

Многочлен Чебышева 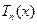степени определяется следующей формулой:

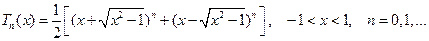(7.1)

Легко проверить, подставляя разные в (7.1), что

.

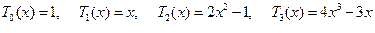В некоторых источниках многочлены Чебышева задают формулой

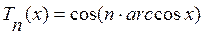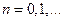, (7.2)

При 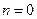имеем 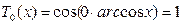. (7.3)

При 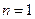, 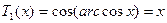. (7.4)

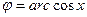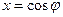Полагая , а , можно написать:

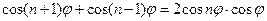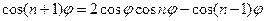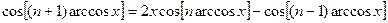или

,

и,

согласно данному определению,

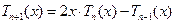, где 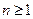. (7.5)

Таким образом, мы получили рекуррентную формулу. В ее справедливости

убеждаемся, находя .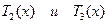

Итак, ;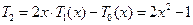

.

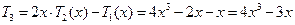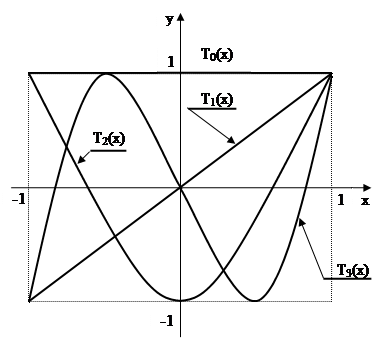Свойства многочленов Чебышева.

Рис. 7.1. К свойствам многочленов Чебышева.

1. При четном (нечетном) многочлен 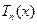содержит только четные (нечетные) степени , т.е. является четной (нечетной) функцией. Это свойство очевидно из формул (7.3)-(7.5).

2. Старший коэффициент многочлена 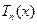при 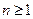равен .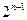

Это свойство очевидно из тех же формул.

3. 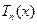имеет действительных корней в интервале (-1,1), выражаемых формулой

.

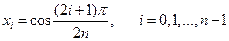Действительно, из определения многочлена Чебышева

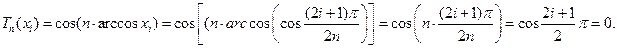
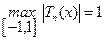, причем 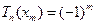, (7.6)

где .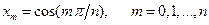

Действительно, согласно определению

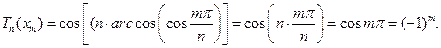
А модуль 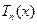не может быть больше единицы потому, что по определению он является косинусом действительного аргумента.

5. Многочлен 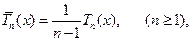(7.7)

среди всех многочленов -ой степени со старшим коэффициентом, равным единице, имеет на отрезке 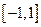наименьшее значение максимума модуля, т.е. для всех многочленов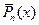 -ой степени со старшим коэффициентом, равным единице, выполняется неравенство

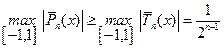. (7.8)

Следствие к cвойству 5. Можно доказать, что если

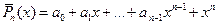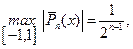и то

.

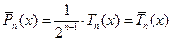(Свойство 5 и следствие к нему принимаем без доказательства).

Благодаря свойству 5 многочлены Чебышева 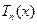называются многочленами, наименее уклоняющимися от нуля.

В качестве узлов, минимизирующих погрешность интерполяции на отрезке 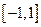берут корни многочлена 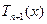т.е. точки

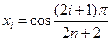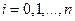, . (7.9)

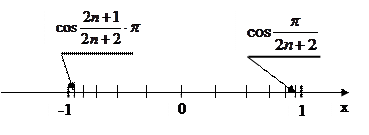Рис.7.2. Качественная иллюстрация расположения

узлов интерполяции (корней многочлена Чебышева)(ср. с рис. 7.3).

Видно, что концы отрезка 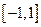здесь не являются узлами интерполяции. Можно доказать, что в силу свойства 2 многочленов Чебышева многочлен

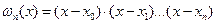, входящий в формулы для оценки погрешностей выражается через 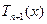следующим образом:

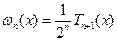, благодаря выбранным узлам интерполяции.

Вспоминая, что

,

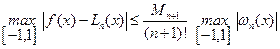и помня свойство 4 многочлена Чебышева, можно написать

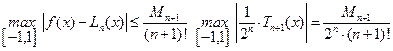, (7.10)

т.к. 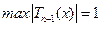. Здесь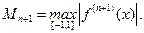

В силу свойства 5 многочлена Чебышева последняя оценка является на отрезке 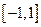наилучшей, т.е. любой другой выбор узлов интерполяции даст оценку хуже. Поэтому выбор узлов интерполяции 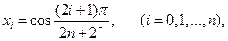является оптимальным для оценки погрешности на отрезке .

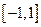В случае интерполирования на произвольном отрезке его переводят в отрезок 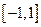соответствующей заменой независимой переменной:

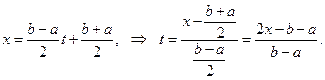(7.11)

При этом узлам интерполяции будут соответствовать точки

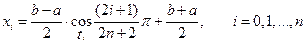. (7.12)

В этом случае согласно последним формулам

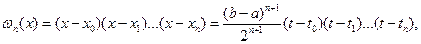
так как 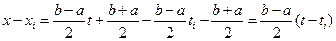, где .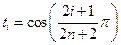

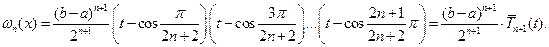
Отсюда с учетом свойства 4 многочленов Чебышева и формул

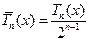или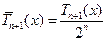

получаем:

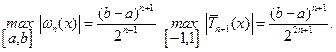
Поэтому при выбранных узлах оценка погрешности интерполяции приобретает вид

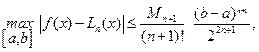(7.13)

где .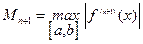

Сравним способы аппроксимации функции 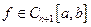многочленом Тейлора 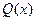и интерполяционным многочленом Лагранжа 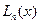с соответствующими узлами. При использовании многочлена Тейлора точку 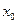берут в середине отрезка , т.е. .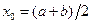

Тогда, в соответствии с формулой

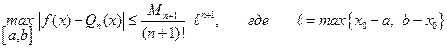
имеем 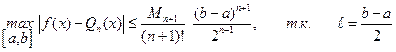. (7.14)

Из сравнения (7.14) и (7.13) видно, что оценка погрешности многочлена Тейлора в 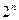раз больше оценки погрешности интерполяционного многочлена Лагранжа 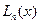с оптимальными узлами.

8. Интерполяция с равноотстоящими узлами.

Оптимальное распределение узлов является неравномерным - узлы сгущаются к концам отрезка и разрежаются в его середине. На практике это неудобно.

Часто используют таблицы, где узлы расположены с постоянным шагом.

Когда задается х, то выбирается несколько ближайших к нему узлов, и производится интерполяция.

Пусть 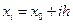- узлы интерполяции; 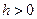- шаг; 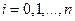; 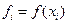- заданные значения функции; 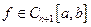, причем .

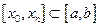Рис. 7.3. Иллюстрация расположения равноотстоящих узлов (ср. с рис. 7.2)

Введем безразмерную переменную

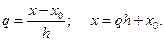(8.1)

Тогда узлу 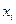соответствует .

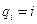Действительно, 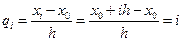. (8.2)

Кроме того, 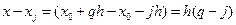; 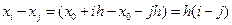. (8.3)

Вернемся к интерполяционным многочленам Лагранжа и выразим их через безразмерную переменную 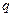(6.16-6.18).

.

.

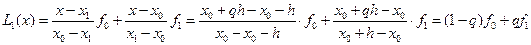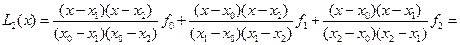
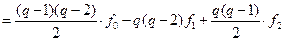В общем случае

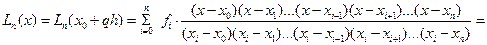
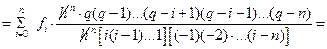
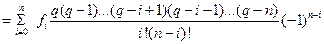(8.4)

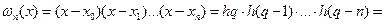
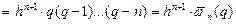. (8.5)

Подставим полученные выражения в формулу для остаточного члена многочлена Лагранжа.

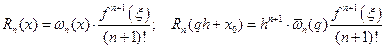. (8.6)

Оценку максимальной погрешности интерполяции на отрезке 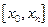с учетом

(8.6) можно записать в виде

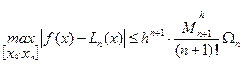, (8.7)

где 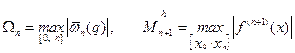(8.8)

Величина 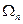не зависит от 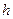. Она может быть заранее вычислена. Например, пусть n = 1. Тогда

.

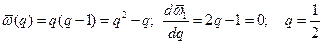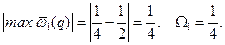
Аналогично находится 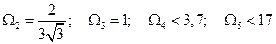. (8.9)

Таким образом, максимальная погрешность интерполяции на отрезке 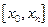, т.е.

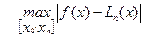есть .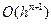

Отсюда следует, что при уменьшении шага 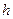вдвое правая часть оценки (8.7) уменьшится по крайней мере в 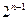раз (здесь учитывается очевидность неравенства ).

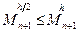Исходя из указанной оценки, следует, что, выбирая шаг 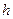таблицы значений функции 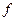на , можно обеспечить заданную точность интерполяции.