Построение кубического сплайна

Пусть на задана непрерывная функция . Введем сетку

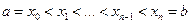и обозначим .

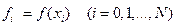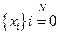Сплайном, соответствующим данной функции и данным узлам , называется функция

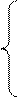
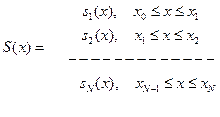, удовлетворяющая следующим условиям:

а) На каждом сегменте 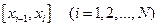функция 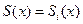является многочленом третьей степени;

б) Функция 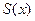, а также ее первая и вторая производные непрерывны на ;

в) .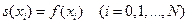

Последнее условие называется условием интерполирования,а сплайн, определяемый условиями а) - в), называется также интерполяционным кубическим сплайном.

Рассмотрим способ построения сплайна.

На каждом из отрезков 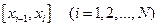будем искать функцию 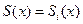в виде многочлена третьей степени.

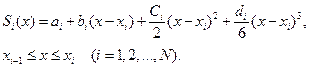(11.1)

где 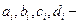коэффициенты, подлежащие определению.

Смысл этих коэффициентов становится видным из дифференцирования (11.1).

.

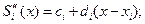
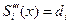Видим, что производные на i-ом сегменте определяют соответствующие коэффициенты:

.

Из условий интерполирования 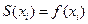получаем, что .

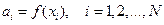Кроме того, 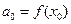. Таким образом, все 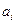найдены. Перепишем теперь (11.1) для функции 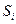в точке 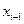, помня, что из выписанных выше определений и формул

;

;

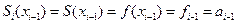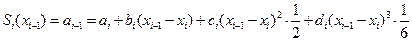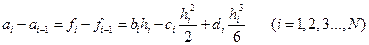. (11.2)

Из условий непрерывности первой производной

,

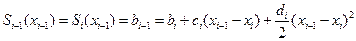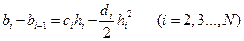(11.3)

Из условия непрерывности второй производной получаем:

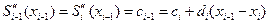
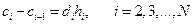. (11.4)

Объединив (11.2-11.4), получаем систему 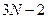уравнений относительно 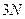неизвестных .

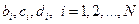Два недостающих уравнения получают, задавая те или иные граничные условия для 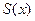. Например, можно потребовать, чтобы функция удовлетворяла условиям 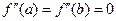, что равносильно .

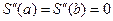Отсюда 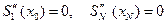, и

.

.

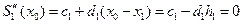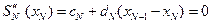Таким образом, приходим к замкнутой системе уравнений для определения

коэффициентов кубического сплайна:

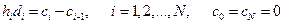(11.5)

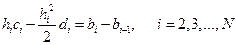, (11.6)

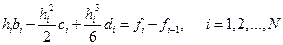. (11.7)

Исследование оценок погрешности приближения сплайнами дает такое выражение:

,

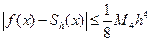где 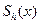- кубический сплайн, построенный на сетке ,

.

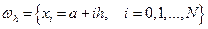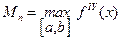12. Численное дифференцирование.

Как мы помним, производной функции 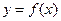называется предел

отношения приращения функции 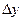к приращению аргумента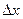

при :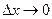

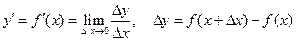. (12.1)

В численных расчетах на ЭВМ значение 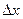полагают равным конечному числу 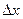(например, шагу таблицы), и делят на него соответствующее приращение функции. За производную принимают его приближенное значение :

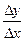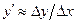. (12.2)

Это соотношение называется аппроксимацией производной с помощью

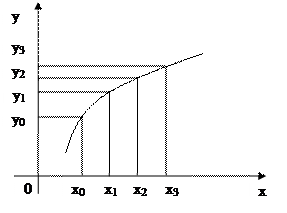отношения конечных разностей.

Рис. 12.1. К аппроксимации производной с помощью

отношения конечных разностей

Пусть ф-ция 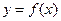задана в табличном виде: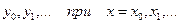

Пусть шаг постоянный и равен .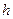

В зависимости от способа вычисления конечных разностей для производной в одной и той же точке получаются разные формулы:

а) с помощью левых разностей

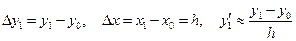; (12.3)

б) с помощью правых разностей

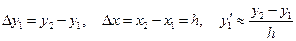; (12.4)

в) с помощью центральных разностей

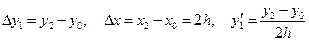. (12.5)

Подобным образом могут быть найдены производные и высших порядков:

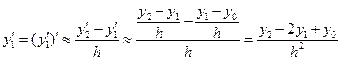. (12.6)

Итак, формула (12.2) позволяет найти приближенные значения производных любого порядка. Какова при этом точность приближения?