Особые случаи численного интегрирования

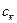
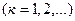а). В ряде случаев подынтегральная функция или ее производные в некоторых внутренних точках отрезка интегрирования терпят разрыв.В этом случае интеграл вычисляют численно для каждого участка непрерывности, и результаты складываются. Например, пр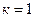и и , , .

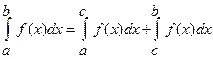б). Вычисление несобственных интегралов. К таким интегралам относятся интегралы, которые имеют хотя бы одну бесконечную границу интегрирования или подынтегральную функцию, обращающуюся в бесконечность хотя бы в одной точке отрезка интегрирования.

Рассмотрим сначала интеграл с бесконечной границей интегрирования, например

.

Возможны несколько приемов вычисления таких интегралов.

1). Можно попытаться ввести замену переменных

Как видно, интервал интегрирования из 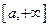превратился в отрезок 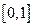. При этом подынтегральная функция и первые ее производные до некоторого порядка должны оставаться ограниченными.

2). Бесконечную границу заменяют некоторым достаточно большим числом в так, чтобы принятое значение интеграла отличалось от исходного на некоторый малый остаток, т.е.

.

Eсли функция обращается в 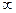в некоторой точке 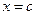конечного отрезка интегрирования, то можно попытаться выделить особенность, представив

подынтегральную функцию в виде суммы . При этом одна из новых функций, например, 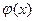ограничена, а 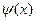имеет особенность в данной точке, но интеграл (несобственный) от нее может быть вычислен непосредственно по формулам. Тогда численным методом вычисляется интеграл только от ограниченной функции .

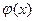Кратные интегралы. Ограничимся рассмотрением двойных интегралов вида

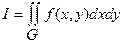. (13.23)

Одним из простейших способов вычисления этого интеграла является метод ячеек. Рассмотрим сначала случай, когда областью интегрирования является прямоугольник: 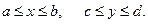По теореме о среднем среднее значение функции 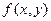равно:

. (13.24)

Будем считать, что среднее значение приближенно равно значению функции в центре прямоугольника, т.е. 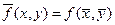. Тогда из (13.24) получаем

выражение для приближенного вычисления двойного интеграла.

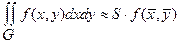, (13.25)

.

Точность вычисления можно повысить, если разбить область 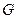на прямоугольные ячейки .

Применяя к каждой ячейке формулу (13.25), получаем

.

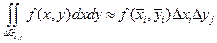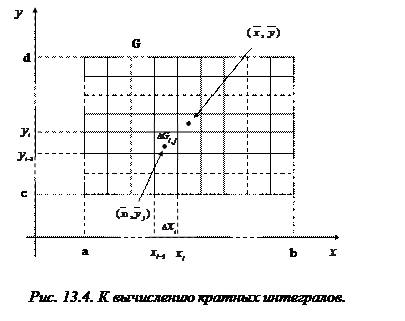
Суммируя эти выражения по всем ячейкам, находим значение двойного интеграла:

. (13.26)

При стягивании ячеек в точки двойная сумма справа стремится к значению интеграла функции 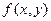, если она непрерывна.

Можно показать, что погрешность такого приближения интеграла для одной ячейки оценивается соотношением

.

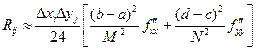Суммируя эти выражения по всем ячейкам и считая все их площади одинаковыми, получаем оценку погрешности метода ячеек в виде

.

.

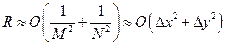Таким образом, формула (13.26) имеет второй порядок точности. Для повышения точности можно использовать методы сгущения узлов сетки. При этом по каждой переменной шаги уменьшают в одинаковое число раз, т.е. отношение должен оставаться постоянным.

В случае если область 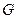не прямоугольная, то в ряде случаев ее целесообразно привести к прямоугольному виду путем замены переменных.

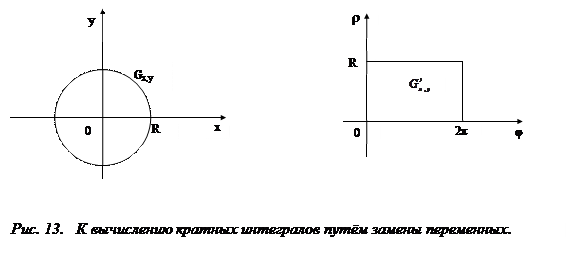
Пример: Вычислить площадь круга радиусом R.

В ВВ

В прямоугольной системе координат площадь круга радиусом R находится интегрированием единичной функции по области G_x,y, ограниченной окружностью радиусом R:

.

Хотя вычисление двукратного интеграла в правой части последнего выражения представляет не очень сложную задачу, она ещё более упрощается, если проделать замену переменных x = ρcosφ, y = ρsinφ и перейти в систему координат ρ, φ. После этого мы приходим к совсем простому двукратному интегралу

.

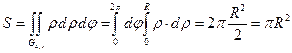Другим распространенным методом вычисления кратных интегралов является сведение их к последовательному вычислению определенных интегралов.

Для прямоугольной области можно записать:

.

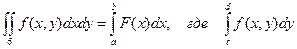Для вычисления обоих определ-х интегралов могут быть использованы рассмотренные ранее численные методы.

Если область 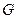имеет более сложную структуру, то она либо приводится к прямоугольному виду с помощью замены переменных, либо разбивается на простые элементы.