Учет погрешностей в арифметических операциях

Принимается за очевидное, что если с = а + b и с^* = а^* + b^* или с^* = а^* - b^* из с = а –b, то

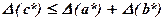(2.4)

и, следовательно, в качестве предельной абсолютной погрешности естественно взять

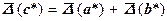(2.5).

Таким образом, при сложении и вычитании двух приближенных чисел их предельные абсолютные погрешности складываются.

Рассмотрим пример.

Пусть а^* = 100 ± 5; b^* = 50 ± 5;

;

.

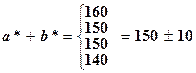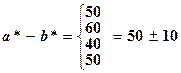Здесь брались граничные случаи. Понятно, что если будем брать значения а^* или b^* внутри интервалов 100 ± 5 и 50 ± 5 соответственно, сумма или разность будут попадать в пределы максимального интервала D с^*.

Подобные рассуждения можно проводить и для произведения двух приближенных чисел а^*× b^*, их частного 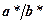и, в общем случае, для любой дифференцируемой функции от этих приближенных чисел. Получающиеся при этом формулы очень напоминают уже известные нам формулы математического анализа. Вспомним формулу для полного дифференциала функции z двух переменных x и y

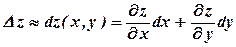. (2.6).

В действиях с приближенными числами пользуются такой же формулой, только частные производные берут по модулю.

Выведем формулу (2.5), воспользовавшись формулой, аналогичной (2.6).

Пусть х = а^*; у = b^* и c^* = a^* ± b^*. Тогда

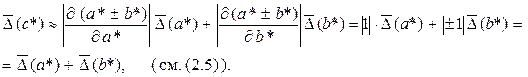
Аналогично выведем формулы для погрешностей произведения и частного приближенных чисел а^* и b^*, используя формулу 2.6. Пусть u* = (a* × b*). Тогда

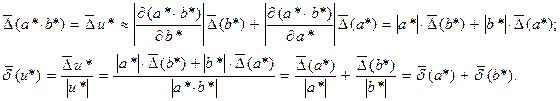(2.7).

Пусть теперь .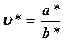

Тогда

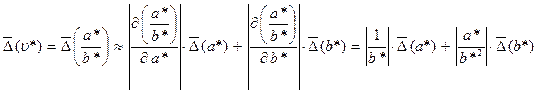
и 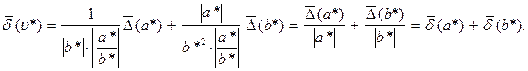(2.8).

Итак:

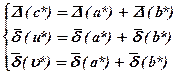
т.е. при сложении и вычитании приближенных чисел складывают предельные абсолютные погрешности, а при умножении и делении приближенных чисел складывают их предельные относительные погрешности.

По аналогии с приведенными примерами могут быть вычислены погрешности приближенных величин, являющихся функциями произвольного количества приближенных чисел. При этом пользуются формулой

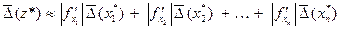(2.9),

где .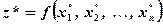

Обратная задача. Часто приходится решать такую задачу: с какой точностью надо задать значения аргументов 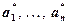функции z = z (a₁, ¼, a_n), чтобы погрешность D z ( 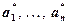), не превосходила заданную величину e ?

Пусть точки (a₁, ¼, a_n) и ( 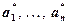), соответствующие истинным и приближенным значениям параметров a_j (j = 1, 2, ¼, n), принадлежат некоторой выпуклой области G и 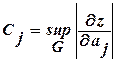. Тогда

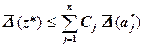(см. 2.9)

Определение. Область G элементов а₁, а₂, ¼, а_п называется выпуклой, если прямая, соединяющая любые две точки этой области, нигде не пересекает границ этой области.

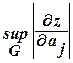- максимальное значение модуля частной производной по аргументу a_j в области определения G функции z (a₁, a₂, ¼, a_n). Очевидно, что любая совокупность 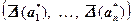абсолютных погрешностей, удовлетворяющих неравенству

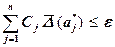(2.10)

будет обеспечивать требуемую точность.

Если функция z зависит только от одного аргумента (п = 1), то имеем неравенство 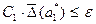и для достижения требуемой точности достаточно взять .

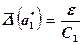В случае п > 1 иногда рекомендуют отвести для погрешности каждого аргумента равную долю, то есть выбрать 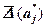из условия 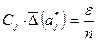, т.е. 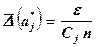. В других случаях предлагают взять погрешности равными и максимально возможными, т.е. положить

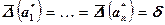, где .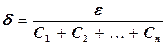

Но это возможно в простейших случаях. Более сложные случаи мы пока рассматривать не будем.