Лекция 17. Производная функции
Понятие производной
Пусть функция 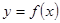 определена в некоторой окрестности точки
определена в некоторой окрестности точки 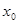 . Предел отношения приращения
. Предел отношения приращения 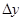 функции в этой точке (если он существует) к приращению аргумента
функции в этой точке (если он существует) к приращению аргумента 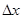 , когда
, когда  , называется производной функции
, называется производной функции 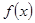 в точке
в точке 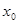 . Обозначается:
. Обозначается: 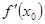 или
или 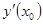 или
или 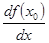 .
.
По определению производной имеем: 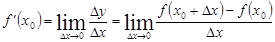 .
.
Вычисление производной называется дифференцированием функции.
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке.
Таблица производных и основные правила дифференцирования
1. 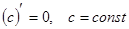
2. 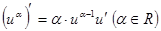 ; в частности
; в частности 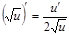
3. 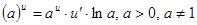 ; в частности
; в частности 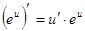
4. 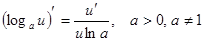 ; в частности
; в частности 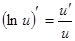
5. 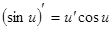 6.
6. 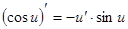
7. 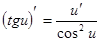 8.
8. 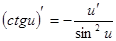
9. 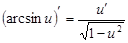 10.
10. 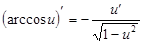
11. 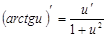 12.
12. 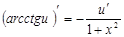
Имеют место следующие основные правила дифференцирования (здесь С- постоянная, а u и v- функции от х, имеющие производные):
13. 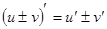 14.
14. 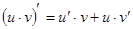
15. 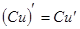 16.
16. 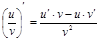
Пусть функция 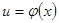 имеет производную в точке
имеет производную в точке 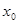 , а функция
, а функция 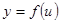 - в точке
- в точке 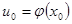 . Тогда сложная функция
. Тогда сложная функция 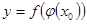 также имеет производную в точке
также имеет производную в точке 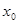 , причем
, причем 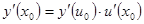 .
.
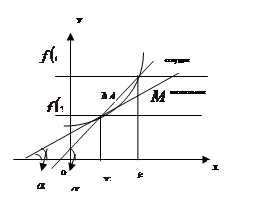 Геометрический смысл
Геометрический смысл
Пусть функция 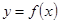 задана на некотором интервале
задана на некотором интервале 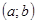 и непрерывна в точке
и непрерывна в точке 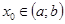 . Выберем какую – нибудь точку
. Выберем какую – нибудь точку 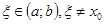 , и через точки
, и через точки 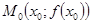 и
и 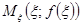 проведем прямую, называемую секущей графика функции и задаваемую уравнением
проведем прямую, называемую секущей графика функции и задаваемую уравнением 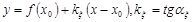 Если окажется, что существует предел
Если окажется, что существует предел 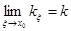 , то секущая при
, то секущая при 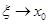 стремится занять предельное положение в виде прямой
стремится занять предельное положение в виде прямой 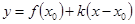 , которую называют касательной к графику функции
, которую называют касательной к графику функции 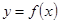 в точке
в точке 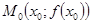 . Поскольку
. Поскольку 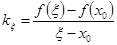 , то существование предела
, то существование предела 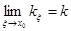 равносильно существованию производной
равносильно существованию производной 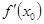 и численному равенству
и численному равенству 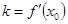 . Этим и определяется геометрический смысл производной, а именно:
. Этим и определяется геометрический смысл производной, а именно:
существование производной 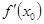 означает наличие касательной к графику функции
означает наличие касательной к графику функции 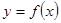 в точке
в точке 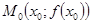 , а величина производной
, а величина производной 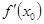 равна угловому коэффициенту этой касательной (тангенсу угла наклона касательной к оси абсцисс) так, что уравнение касательной имеет вид
равна угловому коэффициенту этой касательной (тангенсу угла наклона касательной к оси абсцисс) так, что уравнение касательной имеет вид 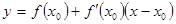 .
.
Физический смысл
Если некий физический процесс описывается функциональной зависимостью 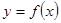 , то отношение
, то отношение 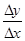 возможно трактовать как среднюю скорость изменения переменной у по отношению к переменной х. Предел
возможно трактовать как среднюю скорость изменения переменной у по отношению к переменной х. Предел 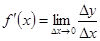 в этом случае можно трактовать как мгновенную скорость изменения переменной у относительно переменной х в точке
в этом случае можно трактовать как мгновенную скорость изменения переменной у относительно переменной х в точке 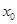 .
.
Например, если физическое тело, движется прямолинейно, проходит за время 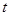 путь
путь 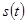 , то его средняя скорость на участке от
, то его средняя скорость на участке от 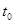 до
до 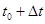 есть
есть 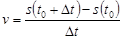 , а мгновенная скорость равна
, а мгновенная скорость равна 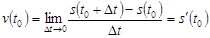 .
.
Логарифмическая производная
При нахождении производных от функций вида 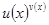 , а также других громоздких выражений, допускающих логарифмирование (произведение, частное и извлечение корня), удобно применять метод логарифмического дифференцирования.
, а также других громоздких выражений, допускающих логарифмирование (произведение, частное и извлечение корня), удобно применять метод логарифмического дифференцирования.
Метод логарифмического дифференцирования позволяет легко найти производную от сложной функции вида 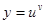 , где u и v- функции аргумента х. Логарифмируя обе части исходного равенства, получим
, где u и v- функции аргумента х. Логарифмируя обе части исходного равенства, получим 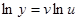 .
.
Дифференцируя это соотношение, имеем 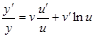 .
.
Умножая обе части равенства на у и заменяя затем у через 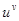 , получаем окончательно:
, получаем окончательно: 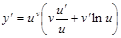 .
.
Производная неявной функции
Пусть функция 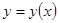 , имеющая производную в точке х, задана неявно уравнением
, имеющая производную в точке х, задана неявно уравнением 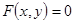 . Тогда производную
. Тогда производную 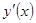 этой функции можно найти следующим образом:
этой функции можно найти следующим образом:
1. Находим производную от левой части равенства, рассматривая при этом у как функцию от х, и приравниваем её нулю.
2. Решаем полученное уравнение относительно 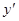 ; в результате будем иметь выражение производной от неявной функции в виде
; в результате будем иметь выражение производной от неявной функции в виде 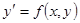 .
.
Производная функции, заданной параметрически
Пусть функция у аргумента х задаётся при помощи пара-
метрических соотношений 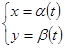 причем
причем 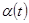 и
и 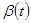 - дифференцируемые функции аргумента t и
- дифференцируемые функции аргумента t и 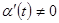 . Производная от у по х находится путем дифференцирования
. Производная от у по х находится путем дифференцирования 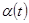 и
и 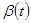 , откуда:
, откуда: