Лекция 18. Дифференциал функции. Дифференциал сложной функции
Понятие дифференциала
Дифференциалом dy функции y=f(x) называется произведение производной этой функции на приращение независимой
переменной 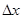 , т.е.
, т.е.  .
.
Дифференциал независимой переменной  , по определению, равен приращению независимой переменной
, по определению, равен приращению независимой переменной 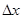 . Поэтому
. Поэтому 
 (1)
(1)
т.е. дифференциал функции равен произведению производной функции на дифференциал независимой переменной.
Формула (1) показывает, что для нахождения дифференциала функции достаточно найти производную этой функции и полученное выражение умножить на  .
.
Операция нахождения дифференциала так же, как и операция нахождения производной, называется дифференцированием.
Применение дифференциала к приближенным вычислениям
Перепишем формулу 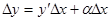 в виде:
в виде:  , где
, где 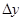 -приращение функции,
-приращение функции,  - дифференциал функции,
- дифференциал функции, 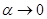 при
при  . Тогда
. Тогда 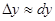 , т. е. приближенное значение приращения функции совпадает и её дифференциалом.
, т. е. приближенное значение приращения функции совпадает и её дифференциалом.
При достаточно малом 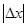 приближённое равенство
приближённое равенство 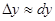 обладает достаточно высокой степенью точности. Отсюда находим:
обладает достаточно высокой степенью точности. Отсюда находим:  или
или 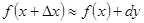 . Перепишем последнее равенство, используя определение дифференциала:
. Перепишем последнее равенство, используя определение дифференциала:  .
.
Это соотношение часто используется в приближенных вычислениях.
 Геометрический смысл дифференциала
Геометрический смысл дифференциала
Для выяснения геометрического смысла дифференциала к графику функции  в точке М(х,у) проведём касательную МТ, обозначив через φ её угол наклона к положительному направлению оси ОХ.
в точке М(х,у) проведём касательную МТ, обозначив через φ её угол наклона к положительному направлению оси ОХ.
Так как 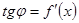 , то
, то 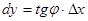 . Поэтому из треугольника MLN следует, что дифференциал dy есть приращение ординаты касательной, соответствующее приращению аргумента
. Поэтому из треугольника MLN следует, что дифференциал dy есть приращение ординаты касательной, соответствующее приращению аргумента 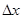 .
.
Замечая, что 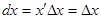 , т.е. что дифференциал независимой переменной равен её приращению, получаем
, т.е. что дифференциал независимой переменной равен её приращению, получаем  .
.
Таким образом , дифференциал функции равен произведению её производной на дифференциал (или приращение) независимой переменной. Т. о. 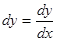 , т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.
, т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.
Дифференциал сложной функции
Найдем выражение для дифференциала сложной функции. Пусть 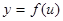 , где
, где  , причём
, причём  имеет производную по
имеет производную по  - по х. Тогда по правилу дифференцирования сложной функции
- по х. Тогда по правилу дифференцирования сложной функции  . Следовательно,
. Следовательно, 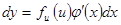 . Но
. Но  . Поэтому
. Поэтому 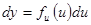 .
.
Таким образом, дифференциал сложной функции имеет тот же вид, какой он имел бы в том случае, если бы промежуточный аргумент её был независимой переменной. Иначе говоря, форма записи дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство дифференциала называется инвариантностью формы дифференциала.
Производные и дифференциалы высших порядков
Производная 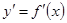 функции
функции 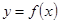 есть также функция от х и называется производной первого порядка. Если функция
есть также функция от х и называется производной первого порядка. Если функция 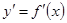 дифференцируема, то ее производная называется производной второго порядка и обозначается
дифференцируема, то ее производная называется производной второго порядка и обозначается  , то есть
, то есть  . Производная n – го порядка называется производная от производной
. Производная n – го порядка называется производная от производной  - го порядка:
- го порядка:  . Производные порядка выше первого называются производными высших порядков.
. Производные порядка выше первого называются производными высших порядков.
