Лекция 10. Степенные ряды
Определение:Ряд 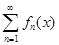 (1), члены которого функции от х, называется функциональным.
(1), члены которого функции от х, называется функциональным.
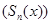 - последовательность частичных сумм функционального ряда.
- последовательность частичных сумм функционального ряда. 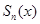 =
= 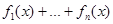 ,
, 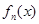 -n-член функционального ряда, S(x)-сумма функционального ряда.
-n-член функционального ряда, S(x)-сумма функционального ряда.
Определение:Если последовательность 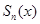 с областью определения G имеет область сходимости D и сходится на D к некоторой функции
с областью определения G имеет область сходимости D и сходится на D к некоторой функции 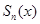 , то есть
, то есть  на D, то говорят, что ряд (1) сходится на множестве D, а S(x)- cумма этого ряда.
на D, то говорят, что ряд (1) сходится на множестве D, а S(x)- cумма этого ряда.
Определение:функциональный ряд (1)называется абсолютно сходящийся в некоторой точке 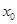 , если в этой точке сходится абсолютно, соответствующий числовой ряд
, если в этой точке сходится абсолютно, соответствующий числовой ряд 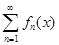 .
.
Определение: сходящийся функциональный ряд (1) называется равномерно сходящийся в некоторой области Х, если для каждого сколь угодно малого числа 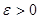 , найдется такое целое число N>0, что при
, найдется такое целое число N>0, что при  выполняется неравенство
выполняется неравенство 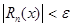 для
для 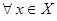 .
.
Признак равномерной сходимости функционального ряда(признак Вейерштрасса) Если функции 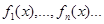 по абсолютной величине не превосходят в некоторой области Х положительных чисел
по абсолютной величине не превосходят в некоторой области Х положительных чисел 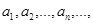 причем числовой ряд:
причем числовой ряд:  сходится, то функциональный ряд
сходится, то функциональный ряд 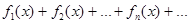 в этой области сходится равномерно.
в этой области сходится равномерно.
Степенные ряды
Определение:Степенным рядом называется ряд вида: (1)  , где
, где 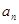 - числа, называемые коэффициентами степенного ряда.
- числа, называемые коэффициентами степенного ряда.
При а=0 степенной ряд имеет вид:  .
.
Теорема Абеля.Если степенной ряд сходится в некоторой точке 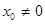 , то он сходится, и притом абсолютно, и во всех точках х, для которых
, то он сходится, и притом абсолютно, и во всех точках х, для которых 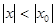 , если же этот ряд расходится в некоторой точке
, если же этот ряд расходится в некоторой точке  , то он расходится и во всех точках х, для которых
, то он расходится и во всех точках х, для которых  .
.
Определение: Число R- половина длины интервала сходимости- называется радиусом сходимости степенного ряда.
Замечание:В частных случаях радиус сходимости ряда R может быть равен нулю или бесконечности. Если R=0, то степенной ряд сходится лишь при х=а; если же  , то ряд сходится на всей числовой оси.
, то ряд сходится на всей числовой оси.
Для отыскания интервала и радиуса сходимости степенного ряда можно пользоваться одним из следующих способов.
1. Если среди коэффициентов ряда 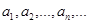 нет равных нулю, то есть ряд содержит все целые положительные степени разности х-а, то:
нет равных нулю, то есть ряд содержит все целые положительные степени разности х-а, то: 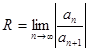 при условии, что этот предел (конечный или бесконечный) существует.
при условии, что этот предел (конечный или бесконечный) существует.
2. Если исходный ряд имеет вид: 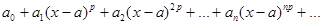 , (где р- некоторое определенное целое положительное число: 2,3,… ), то:
, (где р- некоторое определенное целое положительное число: 2,3,… ), то: 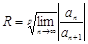 .
.
3. Если среди коэффициентов ряда есть равные нулю и последовательность оставшихся в ряде показателей степени разности х-а любая (то есть не образует арифметическую последовательность, как в предыдущем случае), то радиус сходимости можно находить по формуле:  (причем используются только значения
(причем используются только значения 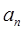 , отличные от нуля (эта формула пригодна и в случаях 1 и 2)).
, отличные от нуля (эта формула пригодна и в случаях 1 и 2)).
4. Во всех случаях интервал сходимости можно находить, применяя непосредственный признак Даламбера или признак Коши к ряду, составленному из абсолютных величин членов исходного ряда.
Записав ряд в виде: 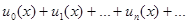 (здесь
(здесь 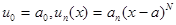 , где зависимость N от n может быть любой, причем через
, где зависимость N от n может быть любой, причем через 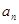 обозначен не коэффициент при
обозначен не коэффициент при 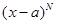 , а коэффициент n-го члена ряда), находят интервал сходимости из неравенств:
, а коэффициент n-го члена ряда), находят интервал сходимости из неравенств: 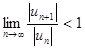 или
или 
