Пространство состояний

Пространство состояний (ABCD-форма) - матричная форма записи системы ДУ САУ адаптированная для теории управления путем выделения из формы Коши алгебраических уравнений связывающих внутренние координаты САУ с выходной(ыми). Применяется для описания САР большого порядка, как правило, с несколькими входами / выходами и с перекрестными связями.

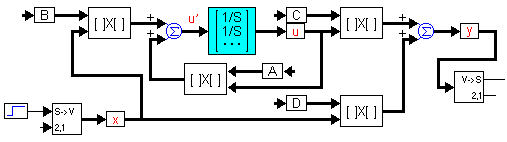
Изображенная на рисунке блок-схема позволяет решить систему ДУ представленную в форме "Пространства состояний":

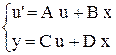(3)

где:

• x_{m x 1} - вектор входных переменных;
• y_{k x 1} - вектор выходных переменных;
• u_{n x 1} - вектор переменных состояния (фазовых координат системы);
• A_{n x n} - матрица коэффициентов системы;
• B_{n x m} - матрица входных коэффициентов (матрица управления);
• C_{k x n} - матрица выходных коэффициентов;
• D_{k x m} - матрица коэффициентов пропорциональных каналов (матрица компенсации);
• n - порядок системы; m - кол-во входов; k - кол-во выходов (m<n).

О форме "Пространство состояний":

• Это вторая по частоте применений форма записи ДУ в ТАУ.
• Признана стандартом для программ математического моделирования VisSim, Simulink, и т.д., однако в большинстве случаев реализована в SISO-форме (с одним входом и одним выходом). Моделирующие программы для выполнения анализа (символьного или частотного) сводят любую модель пользователя к пространству состояний, заполняя в ходе первых шагов симуляции коэффициенты ABCD-матриц.
• Как правило, используется для построения моделей тех больших не поддающихся модуляризации, но не сложных систем, описание которых оптимально в матричной форме (таких мало). Для записи уравнений используются такие методы как: "Метод контурных токов", "Метод узловых потенциалов", - а так же их эквиваленты для других энергетических доменов (гидравлического, теплового, механического, ...).
• Матричное описание строго формализовано, и не требует понимания физической природы системы. Так же структура модели в "пространстве состояний" не позволяет разобраться во внутренней природе системы. Если эта форма записи ДУ применена обосновано, то модель, скорее всего, будет истинной.

ДУ решенное относительно регулируемой величины y(t) - уравнение движения

Система ДУ (1) может быть преобразована к одному уравнению путем исключения промежуточных координат (обычно выходную координату выражают через координату задания):

.

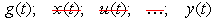Результатом подобного преобразования является уравнение движения системы:

D(p) y(t) = R(p) g(t) - N(p) f(t) , (4)

где:

• D(p) = a₀pⁿ + a₁p^n-1 + ... + a_n-1p + a_n - характеристический полином;
• R(p) = D(p) - Q(p) = b₀p^m + b₁p^m-1 + ... + b_m-1p + b_m - коэффициенты этого полинома определяют влияние задающего воздействия g(t) на регулируемую координату у(t), причем его степень меньше степени характеристического полинома, т.е. m<n;
• N(p) = d₀p^k + d₁p^k-1 + ... + d_k-1p + d_k - коэффициенты полинома определяют влияние помехи f(t) на систему.

ДУ решенное относительно ошибки x(t) - уравнение ошибки

Если система ДУ (1) решается относительно ошибки системы, то получается уравнение ошибки замкнутой системы:

D(p) x(t) = Q(p) g(t) + N(p) f(t) (5)

где: