По теме 3.3 Интегральное исчисление функции
Содержание учебного материала. Интегрирование заменой переменной и по частям в неопределенном интеграле.
Цель работы: закрепить знания, умения и навыки по вычислению неопределенных интегралов заменой переменной и по частям, по интегрированию рациональных функций.
Литература:
[ ОЛ-1 ] Глава 7, § 7.1 – 7.2, стр. 150 - 156,
[ ОЛ-2 ] Глава 7, § 7.1, стр. 76 - 81
[ ОЛ-3 ] Глава 11, § 1 - 7, стр. 188 – 204
Вопросы для повторения:
1. Первообразная. Основное свойство первообразной.
2. Неопределенный интеграл и его геометрический смысл
3. Свойства неопределенного интеграла
4. Таблица интегралов
5. В чем заключается метод непосредственного интегрирования при отыскании неопределенного интеграла?
6. В чем заключается метод замены переменной (метод подстановки) при отыскании неопределенного интеграла?
7. В чем заключается метод интегрирования по частям при отыскании неопределенного интеграла?
Указания к выполнению работы: составьте интеграл, используя параметры своего варианта.
| Вариант | Параметры | Вариант | Параметры | ||||
| a | b | с | a | b | с | ||
| 1 | 6 | -1 | |||||
| 2 | -1 | 7 | -1 | -2 | |||
| 3 | 8 | -1 | |||||
| 4 | -2 | 9 | -2 | -2 | |||
| 5 | -3 | 10 | -3 | -2 |
Таблица интегралов
 | 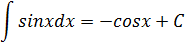 | 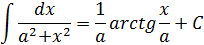 |
 |  | 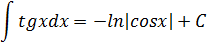 |
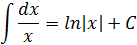 |  |  |
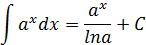 | 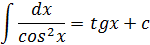 | 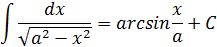 |
 | 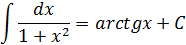 | 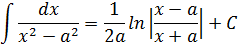 |
Свойства неопределенного интеграла:
 ;
;
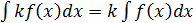 ;
;
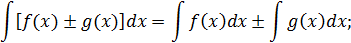
 ;
;
Формула интегрирования по частям: 
Задания
1. Вычислить неопределенный интеграл методом замены переменной:
а)  б)
б) 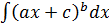 в)
в) 
г)  д)
д) 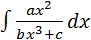 е)
е) 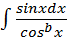
2. Вычислить неопределенный интеграл по частям:
а)  б)
б) 
Практическая работа №9
По теме 3.3 Интегральное исчисление функции
Содержание учебного материала. Интегрирование рациональных функций. Вычисление определенных интегралов.
Цель работы: закрепить знания, умения и навыки по вычислению определенных интегралов.
Литература:
[ ОЛ-1 ] Глава 7, § 7.3 – 7.7, стр. 156 - 169,
[ ОЛ-2 ] Глава 7, § 7.2, стр. 81 - 84
[ ОЛ-3 ] Глава 12, § 1 - 4, стр. 205 – 212
Вопросы для повторения:
1. Определенный интеграл. Формула Ньютона-Лейбница
2. Геометрический смысл определенного интеграла
3. Свойства определенного интеграла
4. Таблица интегралов
5. В чем заключается метод непосредственного интегрирования при отыскании определенного интеграла?
6. В чем заключается метод замены переменной (метод подстановки) при отыскании определенного интеграла?
7. В чем заключается метод интегрирования по частям при отыскании определенного интеграла?
Указания к выполнению работы: составьте интеграл, используя параметры своего варианта.
| Вариант | Параметры | Вариант | Параметры | ||||
| a | b | с | a | b | с | ||
| 1 | 6 | -1 | |||||
| 2 | 7 | -2 | |||||
| 3 | 8 | -1 | |||||
| 4 | 9 | -2 | |||||
| 5 | 10 | -2 |
Таблица интегралов
 | 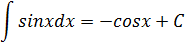 | 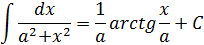 |
 |  | 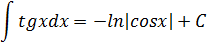 |
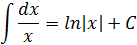 |  |  |
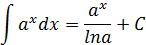 | 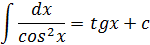 | 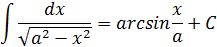 |
 | 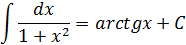 | 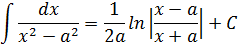 |
Задания
1. Вычислить интеграл от рациональной функции:
а)  а)
а) 
2. Вычислить определенный интеграл методом замены переменной:
а)  б)
б) 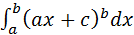 в)
в) 
г) 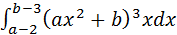 д)
д) 
3. Вычислить определенный интеграл по частям:
а)  б)
б) 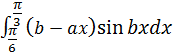
Практическая работа №10
