Определение четырехугольника
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки – сторонами четырехугольника.
З а д а ч а. На рисунке 1–3 представлены три фигуры, каждая из которых состоит из четырех точек и четырех последовательно соединяющих их отрезков. Какая из этих фигур является четырехугольником?
Р е ш е н и е. Четырехугольником является только фигура на рис. 3, так как у фигуры на рис. 1 точки А, В, С лежат на одной прямой, а у фигуры на рис. 2 отрезки ВС и АD пересекаются.
Вершины четырехугольника называются соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противоположные вершины четырехугольника, называются диагоналями. У четырехугольника на рисунке диагоналями являются АС и ВD.
Стороны четырехугольника, исходящие из одной вершины, называются соседними сторонами. Стороны, не имеющие общего конца, называются противолежащими сторонами. У четырехугольника на рис. 4 противолежащими являются стороны АВ и СD, ВС и АD.
Четырехугольник обозначается указанием его вершин. Например, четырехугольник на рис. 4 обозначается так: АВСD. В обозначении четырехугольника рядом стоящие вершины должны быть соседними. Четырехугольник АВСD на рис. 4 можно также обозначить как ВСDА или СDАВ. Но нельзя обозначить АВDС (В и D – не соседние вершины.)
 Рис. 1 Рис. 1 | 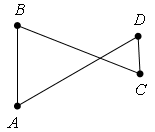 Рис. 2 Рис. 2 | 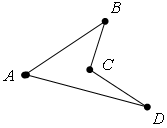 Рис. 3 Рис. 3 |
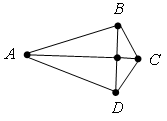 Рис. 4 Рис. 4 |
– Обозначьте данный четырехугольник латинскими буквами (рис. 5).
– Как называется отрезок АС?
– На какие фигуры делит диагональ АС четырехугольник АВСD? (На два треугольника.)
– Чему равна сумма углов в треугольнике?
– Как вы думаете, чему будет равна сумма всех углов данного четырехугольника? – Объясните, как вы рассуждали. 180° + 180° = 360° – Проверьте свое предположение; измерьте углы четырехугольника и запишите их сумму.  А = 50°; А = 50°; 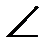 С = 80°; С = 80°; 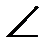 В = 115°; В = 115°; 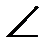 D = 115° D = 115° | 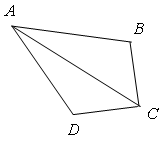 Рис. 5 Рис. 5 |
50° + 80° + 115° + 115° = 360°
– Начертите свои выпуклые четырехугольники и найдите значения сумм их углов.
В ы в о д: сумма углов в выпуклом четырехугольнике равна 360°.
3. Р а б о т а в печатной тетради № 3, з а д а н и е № 71.
| При записи 7001 против часовой стрелки 7 будет в верхнем лепестке, нули в левом и нижнем, а 1 в правом лепестке. По часовой стрелке можно прочитать числа 7100, 710, 100, 71, 10, а также 7, 1, 0, хотя для них порядок прочтения не имеет значения. |  |
VI. Итог урока.
– Что нового узнали на уроке?
– Чему равна сумма углов в треугольнике?
– Чему равна сумма углов в четырехугольнике?
Домашнее задание:учебник, № 424 (4); тетрадь № 3, задание № 72.
У р о к 129 (49).
Соотношение величин: 1 м = 1000 мм, 1 км = 1000 м
Цели: активизировать знания о числах, обозначающих величины «длина», «масса», и соотношениях между ними; ввести новое наименование «километр»; научить читать, записывать четырехзначные числа и вносить их в таблицу разрядов; развивать пространственное мышление учащихся; научить использовать знания основных свойств пространственных фигур при решении нестандартных задач; развивать умение анализировать и выделять главные признаки.
Ход урока
