Определители и их свойства

Определение 1. Определителем второго порядка, соответствующего таблице элементов 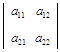, называется число, определяемое равенством

.

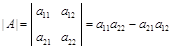Определение 2. Определителем третьего порядка, соответствующего таблице элементов 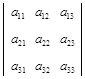, называется число, определяемое равенством

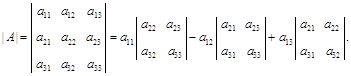
(метод разложения по теореме Лапласа),

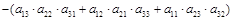
(правило Сариуса - правило «треугольников»).

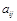Определение 3. Минором элемента определителя п-го порядка называется определитель (п-1) порядка, который получается из определителя путем вычеркивания і-го строки и j-го столбца, на пересечении которых находится элемент .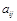

Определение 4. Алгебраическим дополнением 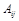элемента 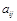определителя называют минор этого элемента, умноженный на , где i – номер строки, а j – номер столбца данного элемента , т.е.

.

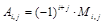Правило: Определительп-го порядка равняется сумме произведений всех элементов любой строки ( или столбца) на соответствующие им алгебраические дополнения.

Свойства определителей

1)Определитель при транспонировании не изменяется.

2)Если в определителе поменять местами любые две строки (столбца), то определитель изменит знак на противоположный.

3)Если определитель имеет два одинаковых столбца (строки), то он равен нулю.

4)Если в определителе все элементы одного столбца (строки) умножить на одинаковое действительное число k, то определитель возрастет также в k раз.

Следствие 1. Общий множитель всех элементов любой строки (столбца) определителя можно вынести за знак определителя.

Следствие 2. Если все элементы любой строки (столбца) определителя равны нулю, то определитель равен нулю.

5)Определитель, у которого соответствующие элементы двух любых строк (столбцов) пропорциональные, равен нулю.

6)Если в определителе элементы i-й строки (k-го столбца) являются суммой двух слагаемых, тогда он равняется сумме двух соответствующих определителей;

7)Определитель не изменится, если ко всем элементам любой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на любое число.

Пример 1. Вычислить определитель второго порядка .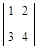

Решение. .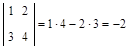

Пример 2. Вычислить определитель третьего порядка, разложив по элементами первой строки:

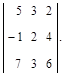
Решение. Разложив определитель по элементам 1-й строки, получим

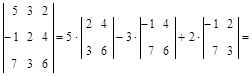
Пример 3. Вычислить определитель по правилу «треугольников»

.

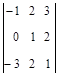Решение.

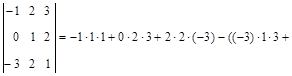
Пример 4. Решить уравнение:

Решение.

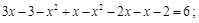
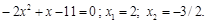
Пример 5. Вычислить определитель четвертого порядка

.

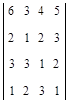Решение. Разложим определитель по элементам первой строки

.
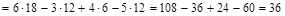