Глава 1 элементы линейной алгебры

СОДЕРЖАНИЕ

Предисловие……………………………………………………………….. 8

Глава 1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ………………………... 10

1.1 Определители и их свойства……………………………..….. 10

1.2 Матрицы и действия над ними………………………………. 14

1.3 Системы линейных алгебраических уравнений……………. 21

1.3.1 Основные понятия……………………………………….. 21

1.3.2 Теорема Кронекера-Капелли……………………………. 22

1.3.3 Матричный способ решения системы………………….. 25

1.3.4 Правило Крамера………………………………………… 27

1.3.5 Метод Гаусса……………………………………………... 29

1.3.6 Решение систем однородных уравнений………………. 31

1.4 Примеры использования линейной алгебры в задачах

экономического содержания………………………………… 39

1.5 Упражнения к главе 1……………………………………….. 44

1.6 Задания для индивидуальной семестровой работы

студентов к главе 1…………………………………………… 49

Глава 2 ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ

ГЕОМЕТРИИ…………………………………………………… 53

2.1 Векторная алгебра…………………………………………… 53

2.1.1 Векторы и действия над ними…………………………… 53

2.1.2 Скалярное произведение векторов……………………... 57

2.1.3. Векторное произведение векторов……………………… 59

2.1.4 Смешанное произведение векторов…………………….. 62

2.1.5 Разложение вектора по базису………………………….. 65

2.1.6 Упражнения к разделу 2.1……………………………….. 68

2.2. Аналитическая геометрия………………………………….. 72

2.2.1 Разновидности уравнения прямой на плоскости………. 72

2.2.2 Уравнения прямой и плоскости в пространстве……….. 74

2.2.3 Кривые линии второго порядка…………………………. 81

2.2.4 Полярная система координат…………………………… 87

2.2.5 Примеры использования элементов аналитической

геометрии в задачах экономического характера………. 89

2.2.6 Упражнения к разделу 2.2……………………………….. 92

2.3 Задания для индивидуальной семестровой работы

студентов к главе 2………………………………………….. 95

Глава 3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ………………… 101

3.1 Функция, предел, непрерывность функций……………… 101

3.1.1 Функция, основные понятия…………………………... 101

3.1.2 Четность, нечетность, периодичность функций……... 102

3.1.3 Основные элементарные функции и их графики……. 103

3.1.4 Предел функции………………………………………... 107

3.1.5 Непрерывность функции. Исследование функции на

непрерывность…………………………………………. 116

3.1.6 Упражнения к разделу 3.1……………………………... 119

3.1.7 Задания для индивидуальной семестровой работы

студентов к разделу 3.1………………………………… 122

3.2 Дифференциальное исчисление функции одной

переменной………………………………………………….. 130

3.2.1 Производная функции в точке………………………… 130

3.2.2 Производная сложной и обратной функции………….. 133

3.2.3 Дифференцирование показательно-степенной

функции…………………………………………………. 134

3.2.4 Дифференцирование неявной функции и функции,

заданной параметрически…………………………….. 135

3.2.5 Логарифмическое дифференцирование……………… 136

3.2.6 Геометрический и физический смысл производной… 137

3.2.7 Дифференциал функции……………………………….. 140

3.2.8 Производные и дифференциалы высших порядков… 143

3.2.9 Упражнения к разделу 3.2……………………………... 147

3.2.10 Задания для индивидуальной семестровой работы

студентов к разделу 3.2………………………………... 151

3.3 Исследование функций с помощью производных………... 156

3.3.1 Монотонность функции. Экстремумы функции…….. 156

3.3.2 Нахождение наибольшего и наименьшего значений

функции на отрезке…………………………………….. 160

3.3.3 Интервалы выпуклости и вогнутости кривой, точки

перегиба…………………………………………………. 161

3.3.4 Асимптоты……………………………………………… 163

3.3.5 Правило Лопиталя……………………………………... 165

3.3.6 Общая схема исследования функции и построение

графиков………………………………………………… 167

3.3.7 Примеры использования дифференциального

исчисления в экономических задачах…………………. 173

3.3.8 Упражнения к разделу 3.3…………………………….. 179

3.3.9 Задания для индивидуальной семестровой работы

студентов к разделу 3.3………………………………… 183

3.4 Дифференциальное исчисление функции нескольких

переменных………………………………………………….. 187

3.4.1 Основные понятия. Область определения функции... 187

3.4.2 Приращение функции 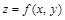. Частные

производные и полный дифференциал функции…… 188

3.4.3 Частные производные и дифференциалы высших

порядков…………………………………………………. 191

3.4.4 Экстремумы функции двух переменных. Наибольшее

и наименьшее значение функции……………………… 193

3.4.5 Производная сложной и неявной функции………….. 197

3.4.6 Использование частных производных в геометрии…. 199

3.4.7 Упражнения к разделу 3.4…………………………….. 202

3.4.8 Задания для индивидуальной семестровой работы

студентов к разделу 3.4………………………………… 206

Глава 4 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ………………………….. 212

4.1 Неопределенный интеграл…………………………………. 212

4.1.1 Первообразная и неопределенный интеграл…………. 212

4.1.2 Основные свойства неопределенного интеграла……... 213

4.1.3 Основные правила интегрирования…………………... 214

4.1.4 Таблица основных интегралов………………………... 214

4.1.5 Основные методы интегрирования функций…………. 216

4.1.6 Интегрирование рациональных дробей………………. 221

4.1.7 Интегрирование тригонометрических функций……. 228

4.1.8 Интегрирование иррациональных функций…………... 234

4.1.9 Упражнения к разделу 4.1……………………………… 238

4.1.10 Задания для индивидуальной семестровой работы

студентов к разделу 4.1……………………………….. 242

4.2 Определенные и несобственные интегралы……………... 253

4.2.1 Определение и свойства определенного интеграла….. 253

4.2.2 Формула Ньютона – Лейбница………………………... 257

4.2.3 Методы интегрирования в определенном интеграле… 259

4.2.4 Несобственные интегралы…………………………….. 261

4.3 Применение определенных интегралов…………………… 264

4.3.1 Вычисление площадей плоских фигур………………… 264

4.3.2 Вычисление длины дуги кривой……………………….. 268

4.3.3. Вычисление объемов тел вращения………………….. 271

4.3.4 Примеры использования интегрального исчисления в

задачах экономического характера……………………. 274

4.3.5 Упражнения к разделам 4.2 и 4.3……………………… 281

4.3.6 Задания для индивидуальной семестровой работы

студентов к разделам 4.2 и 4.3…………………………. 285

Глава 5 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ…………………… 292

5.1 Основные понятия………………………………………….. 292

5.2 Уравнения с разделяющимися переменными……………. 294

5.3 Линейные дифференциальные уравнения первого

порядка и уравнения Бернулли…………………………….. 296

5.4 Однородные дифференциальные уравнения первого

порядка………………………………………………………. 300

5.5 Дифференциальные уравнения второго порядка,

допускающие понижение порядка………………………… 302

5.6 Линейные однородные уравнения с постоянными

коэффициентами……………………………………………. 305

5.7 Пример использования дифференциальных уравнений в

экономических задачах…………………………………….. 307

5.8 Упражнения к главе 5………………………………………. 308

5.9 Задания для индивидуальной семестровой работы

студентов к главе 5…………………………………………. 310

ЛИТЕРАТУРА………………………………………………………….. 313

Предисловие

Современное математическое образование специалистов экономических направлений требует не только знание таких математических дисциплин, как «Высшая математика», «Математическое программирование», «Теория вероятностей и математическая статистика», «Эконометрия», но и навыков решения практических задач соответствующего профиля с использованием математического аппарата, вычислительной техники.

В условиях перехода к Болонской образовательной системе в вузах резко сокращено аудиторное время на изучение разделов высшей математики, значительно увеличена роль самостоятельной работы студентов по овладению дисциплиной, усилена роль прикладной направленности предмета.

В книге кратко изложены необходимые основы математического аппарата и приведены примеры его использования в современных экономических приложениях: элементы линейной и векторной алгебры, аналитической геометрии, дифференциальное исчисление функций одной и нескольких переменных, интегральное исчисление, дифференциальные уравнения.

Именно такой объем знаний актуален сегодня для лиц, получающих образование по экономическим специальностям (в том числе и второе образование), и соответствует требованиям государственных образовательных стандартов по экономическим дисциплинам.

Материал представлен в краткой форме (на уровне понятий, теорем, свойств), основной упор сделан на приобретение навыков использования математического аппарата.

Каждый раздел сопровождается решением достаточного количества типовых упражнений; представлены задания для самостоятельного решения, а также задания для индивидуальной семестровой работы студентов.

В каждом разделе приведены примеры использования конкретного математического аппарата к решению задач экономического содержания, что, по мнению автора, повысит познавательный интерес студентов к учебным занятиям по математике.

Глава 1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ