Л а б о р а т о р н а я р а б о т а 5

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ДВУХ ПАРАМЕТРОВ НА УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Ц Е Л Ь Р А Б О Т Ы - экспериментальное и теоретическое исследование устойчивости в линейной системе при варьировании двух параметров системы.

5.1. краткие сведения из теории

При помощи критериев устойчивости можно установить факт устойчивости или неустойчивости системы, все параметры которой заданы. Однако часто при проектировании и наладке систем возникает более общая задача анализа устойчивости - определение допустимых (по условию устойчивости) пределов изменения некоторых параметров системы. В качестве таких варьируемых параметров обычно рассматривают коэффициенты и постоянные времени управляющего устройства, которые можно целенаправленно изменять при настройке системы. Иногда допустимые пределы изменения определяют и для параметров объекта (если последние изменяются при работе системы).

Допустимые пределы варьирования параметров системы можно определить путем построения областей устойчивости. Область устойчивости выделяет из всех возможных значений варьируемых параметров лишь те значения, при которых система устойчива.

Рассмотрим случай влияния двух параметров на устойчивость системы. При этом все остальные параметры системы должны быть заданы. В качестве варьируемых параметров, как правило, принимают постоянную времени Т одного из конструктивных элементов системы и передаточный коэффициент k разомкнутого контура или одного из элементов. Варьируемые параметры k и Т должны входить в характеристическое уравнение системы линейно, т. е. уравнение не содержит произведений k и Т и их степеней выше первой. Характеристическое уравнение может быть представлено в следующем виде:

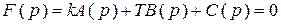, (5.1)

где A(p), B(p), C(p) - полиномы от р, коэффициенты которых не зависят от k и Т.

Согласно общей методике D-разбиения подставим в характеристическое уравнение (5.1) вместо переменной р мнимый корень jω. Тогда получим тождество

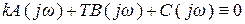, (5.2)

которое при каждом фиксированном значении ω можно рассматривать как уравнение с неизвестными k и Т.

Каждый из трех полиномов, входящих в уравнение (5.2), после возведения jω в четные и нечетные степени можно представить в виде суммы действительной и мнимой частей:

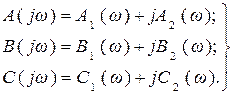(5.3)

Подставляя (5.3) в (5.2) и группируя действительные и мнимые слагаемые, получим

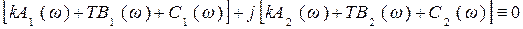. (5.4)

Известно, что комплексная величина равна нулю тогда, когда одновременно равны нулю ее действительная и мнимая части. Поэтому, условие (5.4) эквивалентно двум уравнениям:

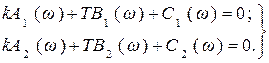(5.5)

Эта система двух уравнений дает возможность определить для каждого фиксированного значения ω два неизвестных k и Т.

Для решения системы (5.5) воспользуемся методом определителей:

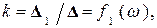(5.6)

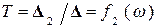(5.7)

где

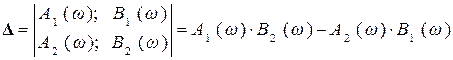; (5.8)

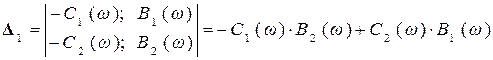; (5.9)

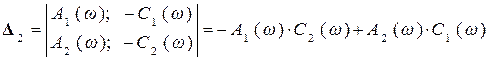. (5.10)

Выражения (5.6) и (5.7) представляют собой уравнение кривой D-разбиения, заданное в параметрической форме. Подставляя в эти выражения различные значения параметра ω (в диапазоне от - 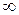до + 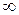), можно построить основную границу области устойчивости.

Так как полиномы А₁(ω), В₁(ω), С₁(ω) - четные функции, а полиномы А₂(ω), В₂(ω), С₂(ω) - нечетные, то определители Δ, Δ₁ и Δ₂ являются нечетными функциями переменной ω; соответственно f₁(ω) и f₂(ω) - четные функции ω. Из этого следует, что кривая D-разбиения при изменении ω от - 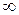до + 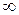проходит дважды через одни и те же точки: первый раз при изменении ω от - 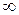до 0 и второй раз - при изменении ω от 0 до + .

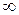Кривая D-разбиения, построенная в плоскости двух параметров, штрихуется по следующему правилу: если главный определитель Δ > 0, то штриховка наносится слева (при движении вдоль кривой в сторону увеличения ω); если определитель Δ < 0, то штриховка наносится справа. Это правило сформулировано применительно к вполне определенному порядку построения кривой D-разбиения: уравнение, получающееся от приравнивания к нулю действительной части, должно быть записано в первой строке системы (5.5); параметр, стоящий на первом месте, необходимо откладывать по оси абсцисс.

Так как при прохождении переменной ω через нуль знак главного определителя Δ меняется на противоположный, то штриховка кривой D-разбиения всегда двойная.

При построении области устойчивости в плоскости двух параметров кроме основной кривой D-разбиения наносят особые прямые. Уравнением особой прямой может служить любое из уравнений (5.5):

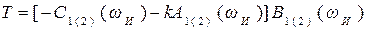, (5.11)

где ω_И - "исключительные" частоты, при которых все три определителя Δ, Δ₁ и Δ₂ одновременно обращаются в нуль или в бесконечность и решения (5.6) и (5.7) становятся неопределенными.

Во многих практических задачах параметры k и Т входят в старший коэффициент a₀ или свободный коэффициент a_n характеристического уравнения системы. В этом случае уравнения двух особых прямых получают приравниванием указанных коэффициентов к нулю:

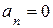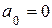; . (5.12)

Первое уравнение соответствует ω_И = 0, а второе - ω_И = .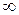

Штриховку особых прямых выполняют по следующим правилам. Особые прямые, соответствующие ω_И = 0 и ω_И = 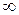, штрихуют один раз, а прямые, соответствующие 0 < ω < 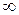, штрихуют дважды. В точках пересечения (или сопряжения) особой прямой с кривой D-разбиения, соответствующих ω = ω_И, заштрихованные стороны прямой и кривой должны быть обращены друг к другу. Причем, если в точке пересечения определитель Δ меняет знак, то штриховка особой прямой переходит на противоположную сторону прямой, если же знак определителя не меняется, то направление штриховки остается прежним.

В данной лабораторной работе необходимо исследовать влияние двух параметров на устойчивость замкнутой системы автоматического управления, передаточная функция которой в разомкнутом состоянии имеет вид:

.

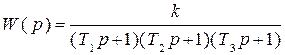5.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Собрать схему моделируемой системы согласно рис. 5.1.

2. Установить коэффициенты k₂ =k₃ =1; Т₂ =0.2 с; Т₃ =0.05 с; k₁ > 0; Т₁ > 0.

3. Изменяя значения параметров k₁ и Т₁ оценить устойчивость замкнутой системы по виду переходного процесса. Результаты исследований занести в таблицу 5.1.

4. Построить графически область устойчивости исследуемой системы в плоскости параметров k и T₁.

5. Нанести на графическое представление области устойчивости точки, полученные в результате экспериментальных исследований.

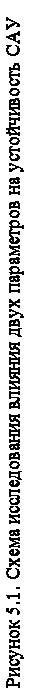
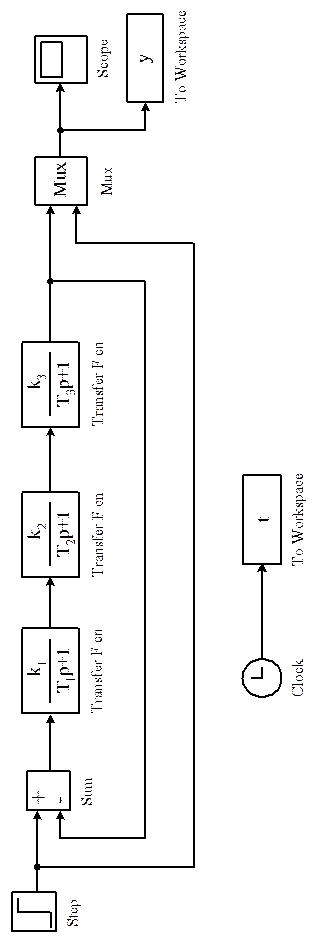
Таблица 5.1.

Т1, c k	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	1.0

5.3. СоДЕРЖАНИЕ ОТЧЕТА

Отчет о лабораторной работе должен содержать:

1. Краткое описание задачи и метода исследования.

2. Схему моделирования.

3. Таблицу экспериментальных исследований.

4. Графическое представление области устойчивости.

5. Выводы по работе с анализом результатов.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Лукас В.А. Теория автоматического управления: Учеб. для вузов. - 2-е изд., перераб. и доп.- М.: Недра, 1990. - 416 с.

2. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования и управления. - М.: Наука, 1972. - 768 с.

3. Васильев Д.В., Чуич В.Г. Системы автоматического управления (примеры расчета). - М.: "Высшая школа", 1967. - 419 с.

4. Сборник задач по теории автоматического регулирования и управления. Под редакцией В.А. Бесекерского, издание пятое, переработаное, издательство "Наука", М., 1978. - 512 с.

Учебное издание

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО КУРСУ

"ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ"

ЧАСТЬ I

(для студентов специальности 7.092501 АУП)

Составители:

ТКАЧЕНКО Валерий Николаевич

ПОПОВ Владислав Александрович

ФЕДЮН Роман Валериевич