Практическая работа 1. понятие множества

Цель.Усвоить связанную с понятиями множество, элемент множества, характеристическое свойство элементов множества, подмножество, равные множества соответствующую математическую символику. Уметь задавать отношения пересечения, объединения, равенства над множествами.

Теоретическая часть

Вопросы к изучению

Понятие множества и элемента множества

2. Пустое множество. Способы задания множеств

3. Отношения между множествами: включение, равенство, пересечение. Подмножество.

4. Изображение отношений между множествами при помощи кругов Эйлера (С/Р)

Основные понятия

Ø множество;

Ø элемент множества;

Ø характеристическое свойство элементов множества;

Ø подмножество;

Ø равные множества.

Обозначения

а Î А – «а принадлежит множеству А»;

b Ï А - «b не принадлежит множеству А»;

А = {1, 2, 3, 4} - запись множества А путем перечисления всех его элементов;

А = { х | х Î N и х > 5} - запись множества А путем указания характеристического свойства его элементов;

А Ì B - « А – подмножество В»;

А = В – «Множества А и В равны».

Практическая часть

Обязательные задания

1. Назовите три элемента множества: а) учебных предметов, изучаемых в начальной школе; б) четных натуральных чисел; в) четырехугольников.

2. В – множество четных чисел. Зная это, запишите с помощью символов следующие предложения: 1) число 20 четное; 2) число 17 не является четным.

3. Запишите, используя символы: а) Число 14 – натуральное; б) Число – 7 не является натуральным; в) Число 0 – рациональное; г) 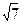- число действительное.

4. Даны числа: 325, 0, - 17, -3,8, 7. Установите, какие из них принадлежат множеству: 1) натуральных чисел; 2) целых чисел; 3) рациональных чисел; 4) действительных чисел.

5. Прочитайте следующие высказывания и укажите среди них истинные: 100 Î N; 2) –8 Î Z; 3) –8 Ï N; 4) 5,36 Î Q; 5) 102 Ï R; 6) 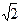ÎQ; 7) –7 Î R; 8) 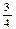ÎN; 9) 0 Î Z.

6. Р – множество натуральных чисел, больших 7 и меньше 14. Выясните, какие из чисел 13, 10, 5, 7, 14 ему принадлежат, а какие не принадлежат. Ответ запишите, используя знаки Î и Ï.

7. А – множество решений уравнения х² + 1 = 0. Верно ли, что А – пустое множество? Приведите примеры уравнения, множество решений которого состоит из: а) одного элемента; б) двух элементов; в) трех элементов.

8. Запишите с помощью знака равенства и фигурных скобок предложения: 1) Х – множество чисел 0, 1, 2, 3, 4, 5; 2) У- множество букв в слове «математика».

9. Множество С состоит из квадрата, круга и треугольника. Принадлежит ли этому множеству диагональ квадрата?

10. Перечислите элементы следующих множеств: А – множество нечетных однозначных чисел; В - множество натуральных чисел, не меньших 5; С – множество двузначных чисел, делящихся на 10.

11. Укажите характеристическое свойство элементов множества: а) {а, е, е, и, о, у, э, ю, я, ы}; б) {23, 22, 21, 20, 19, 18, 17, 16, 15 }; в) {11, 22, 33, 44, 55, 66, 77, 88, 99}.

12. Изобразите на координатной прямой множество решений неравенства ( х- действительное число): х > 5,3; 2) х £ -3,8; 3) – 4,5£ х < 4; 4) 2,7 £ х £ 9.

13. Найдите множество действительных корней уравнения: 1)3х=х+8; 2) 3х+5=3(х+1); 3) 3(5х+10)=30+15х; 4) х (х+16)=0.

14. А - множество двузначных чисел, запись которых оканчивается цифрой 1. Принадлежит ли этому множеству числа 28, 31, 321, 61?

15. Дано множество А = {5, 10, 15, 25}. Укажите два подмножества, равные множеству А.

16. Известно, что элемент асодержится в множестве А и в множестве В. Следует ли отсюда, что: 1) А Ì В; 2) В Ì А; 3) А = В?

17. Известно, что каждый элемент множества А содержится в множестве В. Верно ли, что тогда: 1) А Ì В; 2) А = В?

18. Из множества К = {216, 546, 153, 171, 234} выпишите числа, которые: 1) делятся на 3; 2) делятся на 9; 3) не делятся на 4; 4) не делятся на 5. Есть ли среди полученных подмножеств такое, которое равно множеству К?

19. Установите, в каком отношении находятся множества решений неравенств и сами неравенства: 1) х < 12 и х < 10; 2) х < 12 и х > 15; 3) х < 12 и х > 10; 4) х < 12 и –3х > -36.

20. Изобразите при помощи кругов Эйлера отношения между множествами А и В, если: 1) А – множество четных чисел, В – множество чисел, кратных 3; 2) А - множество квадратов, B- множество прямоугольников; 3) А – множество квадратов, В – множество прямоугольных треугольников; 4) А – множество квадратов, B – множество прямоугольников с равными сторонами.

21. Изобразите при помощи кругов Эйлера отношения между множествами А, В и С, если известно, что: 1) А Ì В и В Ì А; 2) А Ì В, С пересекается с В, но не пересекается с А; 3) А, В и С пересекаются, но ни одно не является подмножеством другого.

Творческие задания

1. Запишите множество, состоящее из скаута и отряда, командиром которого он является.

2. Покажите, что, выполняя задание: «Увеличь каждое нечетное однозначное число в 2 раза», учащиеся встречаются с двумя способами задания множества.

3. Покажите, что, выполняя задание: «Какое число лишнее в ряду: 470, 720, 330, 400, 510, 640», учащиеся, по существу, пользуются понятиями характеристического свойства элементов множества и принадлежности элемента множеству.

4. Приведите примеры трех заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому.

5. О каких теоретико–множественных понятиях идет речь в следующих заданиях, выполняемых учащимися начальных классов: а) Запиши по порядку числа от 10 до 19. Подчеркни и прочитай четные числа; б) Из ряда чисел от 1 до 20 выпиши по порядку числа, которые делятся на 5; в) Запиши три числа, которые при делении на 7 дают в остатке 4.

6. Изобразите на диаграмме Эйлера – Венна следующие множества: множество всех отличников 3–Б класса школы № 5, множество мальчиков этого же класса, множество девочек этого же класса. Покажите на диаграмме фигуру, изображающую множество всех учеников 3-Б класса, фигуру, изображающую множество мальчиков-отличников.

ТЕМА 3. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ (ЛЕКЦИЯ)

Содержание

1. Пересечение множеств

2. Объединение множеств

3. Законы пересечения и объединения множеств (С/Р)

4. Вычитание множеств. Дополнение одного множества до другого

Основная литература [ ];

Дополнительная литература [ ]

Пересечение множеств

Из элементов двух и более множеств можно образовать новые множества. Считают, что эти новые множества являются результатом операций над множествами.

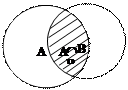Пример

Пусть даны два множества: А = {2, 4, 6, 8 } и В = {5, 6, 7, 8, 9}.

Образуем множество С, в которое включим общие элементы множеств А и В: С = {6, 8 }. Так, полученное множество С называют пересечением множеств А и В.

Определение. Пересечением множеств А и В называется множество, содержащее только такие элементы, которые принадлежат множеству А и множеству В.

Пересечение множеств А и В обозначают А Ç В. Тогда определение можно представить в символической записи:

х Î A Ç B Û х Î A и х Î B.

Если изображать множества А и В при помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной частью.

В том случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто и пишут: А Ç В = Æ.

Замечание. Операция, при помощи которой находят пересечение множеств, называется также пересечением

Ø Нахождение пересечения множеств в конкретных случаях

· Если элементы множеств А и В перечислены, то, чтобы найти А Ç В, достаточно перечислить элементы, которые принадлежат А и В, т.е. их общие элементы.

· Если множества заданы при помощи характеристических свойств элементов, то характеристическое свойство множества А Ç В составляется из характеристических свойств пересекаемых множеств с помощью союза «и».

Пример

Найдем пересечение множества А – четных натуральных чисел и множества В – двузначных натуральных чисел.

Характеристическое свойство элементов множества А – «быть четным натуральным числом», характеристическое свойство элементов множества В – « быть двузначным натуральным числом». Тогда, согласно определению, элементы пересечения данных множеств должны обладать свойством «быть четным и двузначным натуральным числом». Таким образом, множество А Ç В состоит из четных двузначных чисел (союз «и» в данном случае можно опустить). Полученное множество не пусто. Например, 24 Î А Ç В, поскольку число 24 четное и двузначное.

Пример

Найти пересечение множества А – четных натуральных чисел и множества В – натуральных чисел, кратных 4. Данные множества А и В бесконечные, и множество В – подмножество множества А. Поэтому элементами, принадлежащими множеству А и множеству В, будут элементы множества В. Следовательно, А Ç В = В.

Объединение множеств

Для того, чтобы объяснить школьнику, что 2 + 3 = 5, учитель берет 2 красных кружка и 3 синих. Просит перечислить эти кружки, затем предлагает к красным кружкам придвинуть синие (т.е. объединить эти две совокупности, два множества) и пересчитать все кружки совокупности. Устанавливается, что их 5, т.е. 2 +3 = 5. Таким образом, сложение чисел опирается на операцию объединения двух множеств.

В рассмотренном примере объединялись множества, не имеющие общих элементов. В математике приходится выполнять объединение и пересекающихся множеств.

Определение. Объединением множеств А и В называется множество, содержащее такие элементы, которые принадлежат множеству А или множеству В.

Объединение множеств А и В обозначают A È B. В символической записи: х Î A È B Û х ÎA или х Î B.

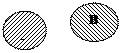Если изобразить пересекающиеся множества при помощи кругов Эйлера, то их объединение изобразится заштрихованной областью (рис. 1). Если множества А и В не пересекаются, то их объединение изображают так (рис. 2).

Рис 1. Рис. 2.