Иррациональных функций
Правило 1. Ввести новую переменную " 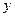 " так, чтобы можно было извлечь все корни, содержащиеся в функции (обычно функция содержит более одного корня; эти корни – разной степени).
" так, чтобы можно было извлечь все корни, содержащиеся в функции (обычно функция содержит более одного корня; эти корни – разной степени).
Пример.
10) 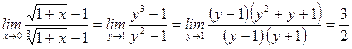 .
.
Мы сделали замену: 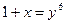 ; при
; при 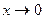
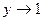 .
.
Правило 2. Перевести иррациональность из числителя в знаменатель или наоборот.
Пример.
11) 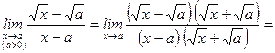
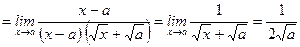 .
.
Умножили числитель и знаменатель на выражение 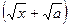 , сопряженное числителю. В результате преобразований корни из числителя "исчезли", но появились в знаменателе.
, сопряженное числителю. В результате преобразований корни из числителя "исчезли", но появились в знаменателе.
Замечание. Задачи такого типа составляются и решаются следующим образом. Берем любые числа 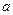 и
и 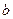 и записываем с:
и записываем с:
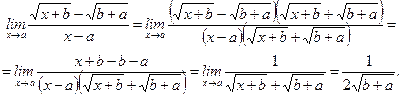
В случае примера 11: 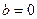 .
.
Правило 3. Разделить числитель и знаменатель на " 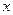 " в наивысшей степени, встречающейся в функции (возможно, после некоторых преобразований функции). Правило применяется в случае, когда
" в наивысшей степени, встречающейся в функции (возможно, после некоторых преобразований функции). Правило применяется в случае, когда 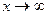 .
.
Пример.
12) 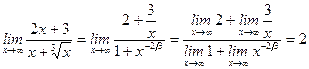 .
.
Задачи для самостоятельного решения
Вычислить пределы.
1) 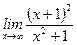 ; 2) ; 2) 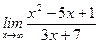 ; 3) ; 3) 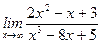 ; 4) ; 4) 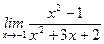 ; 5) ; 5) 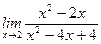 ; 6) ; 6) 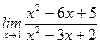 ; 7) ; 7) 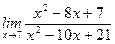 ; 8) ; 8) 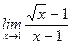 ; ; | 9) 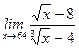 ; 10) ; 10) 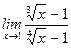 ; 11) ; 11) 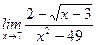 ; 12) ; 12) 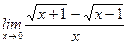 ; 13) ; 13) 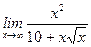 ; 14) ; 14) 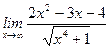 ; 15) ; 15)  . . |
Ответы:
1)1; 2)  ; 3) 0; 4) -2; 5)
; 3) 0; 4) -2; 5)  ; 6) 4; 7)
; 6) 4; 7) 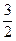 ; 8)
; 8) 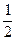 ; 9) 3; 10)
; 9) 3; 10) 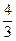 ; 11)
; 11) 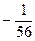 ; 12) 1; 13)
; 12) 1; 13)  ; 14) 2; 15)
; 14) 2; 15) 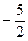 .
.
Занятие 4.
Первый и второй замечательные пределы.
Вычисление пределов вида 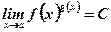 .
.
Бесконечно малые и бесконечно большие величины.
Определения. Первый замечательный предел: 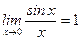 .
.
Второй замечательный предел: 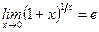 .
.
Следствия из формулы для второго замечательного предела:
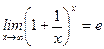 ;
; 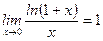 .
.
Обобщения формул для 1-го и 2-го замечательных пределов:
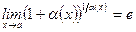 ;
; 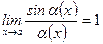 ,
,
где 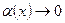 при
при 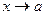 .
.
Нахождение пределов вида 
Правило.
1)Если существует 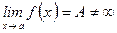 ,
, 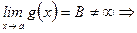
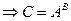 ;
;
2)Если существует 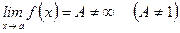 ,
, 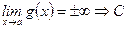 находим непосредственно(
находим непосредственно( 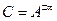 , т.е. величина
, т.е. величина 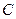 зависит от знака при символе "
зависит от знака при символе "  " и от того,
" и от того, 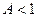 или
или 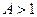 . Таким образом, либо
. Таким образом, либо 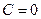 , либо
, либо 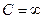 ).
).
3)Если 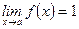 ,
, 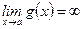 , то полагаем
, то полагаем 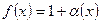 , где
, где 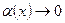 при
при 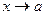 , и находим
, и находим 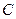 по формуле:
по формуле: 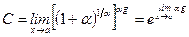 .
.
Бесконечно малые и бесконечно большие величины
Определение 1. Если 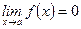
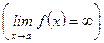 , то
, то 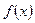 называется бесконечно малой (большой) величиной (или функцией) при
называется бесконечно малой (большой) величиной (или функцией) при 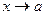 .
.
Определение 2. Если 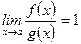 (
( 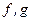 – бесконечно малые), то
– бесконечно малые), то 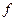 и
и 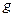 называются эквивалентными бесконечно малыми. Пишем:
называются эквивалентными бесконечно малыми. Пишем: 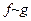 при
при 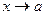 . Говорим: "функция
. Говорим: "функция 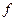 эквивалентна функции
эквивалентна функции 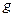 при
при 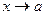 ".
".
Теорема. Пусть 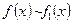 ,
, 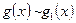 при
при 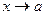 (
( 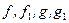 – бесконечно малые функции). Тогда:
– бесконечно малые функции). Тогда:
 .
.
Таблица эквивалентных бесконечно малых функций при 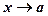 (
( 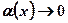 при
при 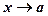 ).
).
1.  ; 8.
; 8. 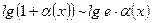 ;
;
2. 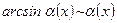 ; 9.
; 9. 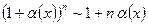
3. 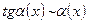 ; (
; ( 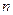 – натуральное число).
– натуральное число).
4.  ;
;
5. 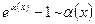 ;
;
6. 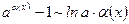 ;
;
7. 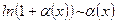 ;
;
Примеры.
1) 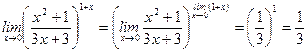 ,
,
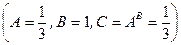 ;
;
2) 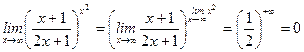 ,
,
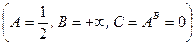 ;
;
3) 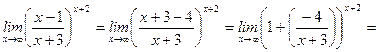
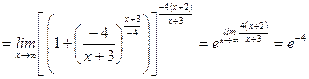 ;
;
4) 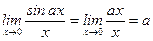 (
( 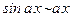 при
при 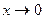 );
);
5) 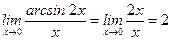 (
( 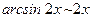 при
при 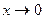 );
);
6) 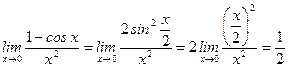 ,
,
( 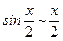 при
при 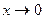 );
);
7) 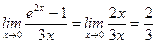 (
( 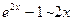 при
при 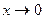 );
);
8) 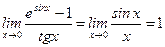 ,
,
( 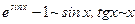 при
при 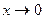 );
);
9) 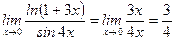 ,
,
( 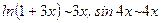 при
при 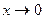 );
);
10) 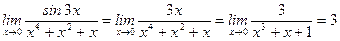 ,
,
( 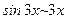 при
при 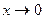 ; сделали преобразование – разделили числитель и знаменатель на "
; сделали преобразование – разделили числитель и знаменатель на " 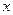 ");
");
11) 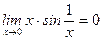 (произведение бесконечно малой функции
(произведение бесконечно малой функции 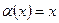 на ограниченную функцию
на ограниченную функцию 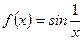 – это бесконечно малая функция, поэтому вышеуказанный предел равен нулю).
– это бесконечно малая функция, поэтому вышеуказанный предел равен нулю).
Задачи для самостоятельного решения
1) 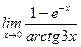 ; 2) ; 2) 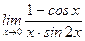 ; 3) ; 3) 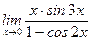 ; 4) ; 4) 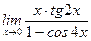 ; 5) ; 5)  ; ; | 6) 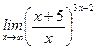 ; 7) ; 7) 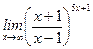 ; 8) ; 8) 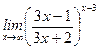 ; 9) ; 9) 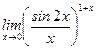 . . |
Ответы: 1) 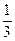 ; 2)
; 2) 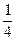 ; 3)
; 3) 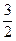 ; 4)
; 4) 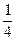 ; 5)
; 5) 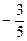 ; 6)
; 6) 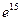 ; 7)
; 7) 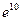 ; 8)
; 8) 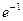 ; 9) 2.
; 9) 2.
Занятие 5.
Точки непрерывности и точки разрыва функции.
Классификация точек разрыва.
