Краткие теоретические сведения. Второй закон Ньютона
Второй закон Ньютона. В рассматриваемых ниже математических моделях физических процессов фундаментальную роль играет второй закон Ньютона. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько — то равнодействующей этих сил) и обратно пропорционально его массе:
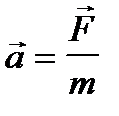 (1)
(1)
Свободное падение тела.Математическая модель свободного падения тела — уравнение второго закона Ньютона с учетом двух сил, действующих на тело — силы тяжести и силы сопротивления среды. Движение является одномерным; проецируя силу тяжести 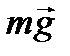 , силу сопротивления
, силу сопротивления 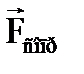 , скорость
, скорость 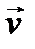 и перемещение
и перемещение 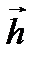 на ось, направленную вертикально вниз, получаем :
на ось, направленную вертикально вниз, получаем :
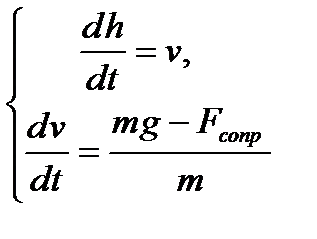 (2)
(2)
Сила сопротивления имеет две составляющие: 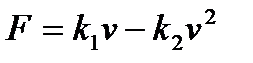 .
.
Коэффициенты 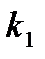 и
и 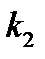 определяется свойствами среды и формой тела. Например, для шара
определяется свойствами среды и формой тела. Например, для шара 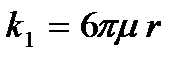 — так называемая формула Стокса, где
— так называемая формула Стокса, где 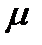 — динамическая вязкость среды,
— динамическая вязкость среды, 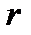 — радиус шара. Обычно принимают
— радиус шара. Обычно принимают 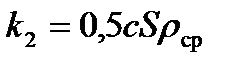 , где S - площадь сечения тела, поперечного по отношению к потоку,
, где S - площадь сечения тела, поперечного по отношению к потоку, 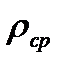 - плотность среды, c — безразмерный коэффициент лобового сопротивления (см. рис. 1). В конкретных задачах можно одной из составляющих силы сопротивления пренебречь (если она значительно меньше другой).
- плотность среды, c — безразмерный коэффициент лобового сопротивления (см. рис. 1). В конкретных задачах можно одной из составляющих силы сопротивления пренебречь (если она значительно меньше другой).
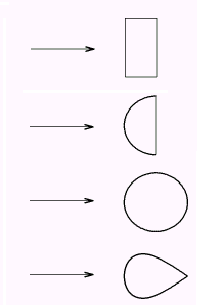 | Диск Полусфера Шар «Каплевидное» тело | c=1,11 c=0,55 c=0,4 c=0,045 |
Рис. 1. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму
Взлет ракеты. Исследуем ситуацию, когда масса тела не является величиной постоянной. Запишем второй закон Ньютона в более общей математической форме.
Построим простейшую модель вертикального взлета ракеты, приняв следующие гипотезы:
1) масса ракеты уменьшается во время взлета по линейному закону:
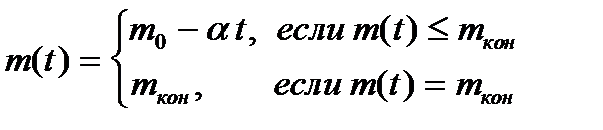 , (3)
, (3)
где m0 ¾ начальная масса ракеты, заправленной топливом; mкон ¾ остаточная масса после полного выгорания топлива;a ¾ расход топлива;
2) Сила тяги двигателя постоянна на всем участке взлета.
3) плотность воздуха r, входящая в коэффициент k2, убывает по мере подъема ракеты по закону r = r0 . 10-bh, где h ¾ высота, b » 5,6 . 10-5 м-1 .
Таким образом, модель будет описываться системой двух дифференциальных уравнений для функций v(t) и h(t):
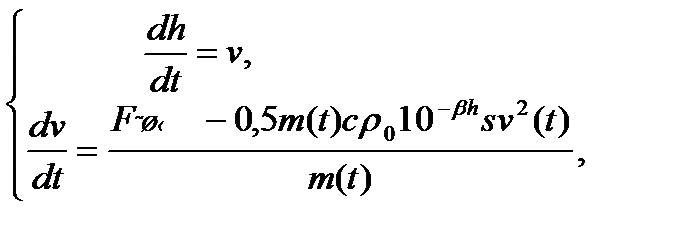 (4)
(4)
Движение тела, брошенного под углом к горизонту.Дифференциальные уравнения модели получаются из второго закона Ньютона проецированием скорости и перемещения на горизонтальную и вертикальную оси координат:
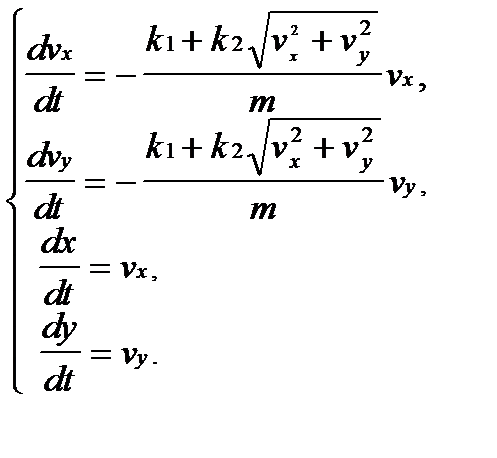
 (5)
(5)
Здесь m ¾ масса тела; v x=vcosa ,vy=vsina - величины проекций начальной скорости v на горизонтальную и вертикальную оси; a ¾ угол начального наклона вектора скорости к горизонту; k1 и k2 – коэффициенты, входящие в в формулу силы сопротивления.
Движение небесных тел.Рассмотрим модель движения космического тела (планеты, кометы, спутника) под действием силы всемирного тяготения в гравитационном поле, создаваемом телом с многократно большей массой.
Примем следующие предположения: «большое» тело находится в начале системы координат, другие тела на движение «малого» тела влияния не оказывают. Дифференциальные уравнения модели имеют вид
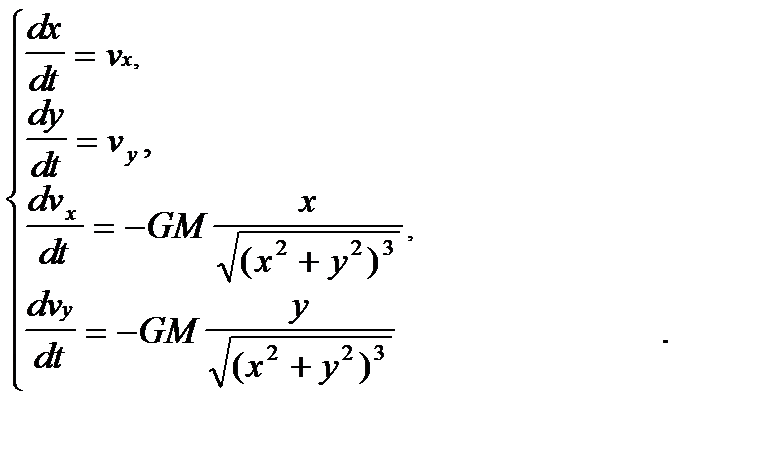 , (6)
, (6)
где M- масса «большого» тела; x, y - координаты «малого» тела, движение которого изучается; vx, vy – величины проекций скорости «малого» тела на горизонтальную и вертикальную оси, G = 6,67. 10-11 м3/кг с2 ¾ гравитационная постоянная .
Обезразмеривание. В задаче о движении небесных тел особенно неудобно работать с размерными величинами, измеряемыми миллиардами километров, секунд и т.д. В качестве величин для обезразмеривания удобно принять характерное расстояние от Земли до Солнца ρ = 1,496∙1011 м, (так называемая астрономическая единица), период круговой орбиты 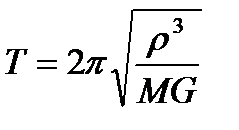 ,соответствующий этому расстоянию, скорость движения по ней
,соответствующий этому расстоянию, скорость движения по ней 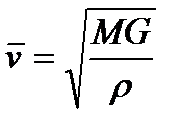 , т.е. принять
, т.е. принять
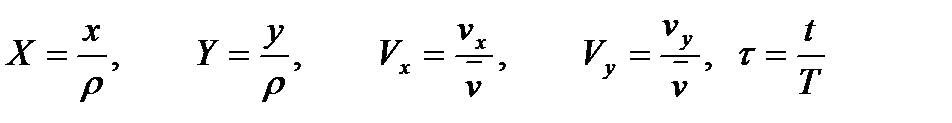
После обезразмеривания получаем
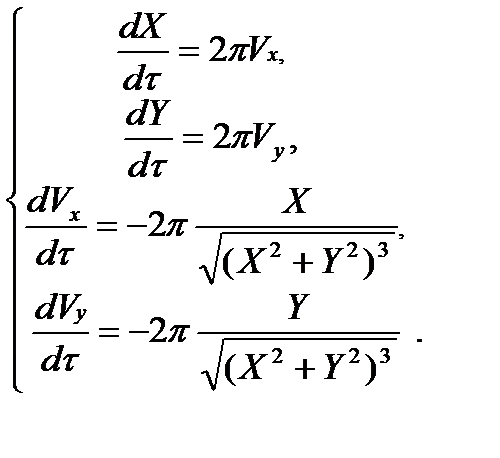 (7)
(7)
В безразмерных переменных уравнения вообще не содержат параметров. Единственное, что отличает разные режимы движения друг от друга – это начальные условия.
Движение заряженных частиц.Рассмотрим модель движения заряженной частицы в кулоновском поле другой заряженной частицы, положение которой фиксировано.
В системе координат, начало которой привязано к «большому» телу, дифференциальные уравнения модели имеют вид
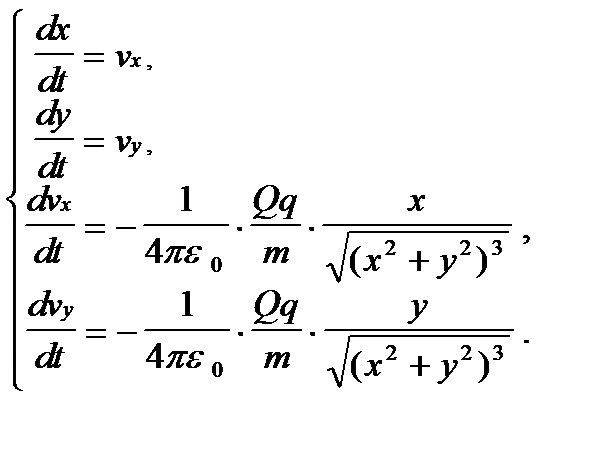 (8)
(8)
Они получаются из второго закона Ньютона и закона Кулона. 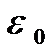 = 0,85 . 10-12 ф/м ¾ электрическая постоянная. Знак “-” в двух последних уравнениях соответствует разноименно заряженным частицам; в случае одноименных зарядов он меняется на “+”. Здесь q и Q ¾ соответственно заряды движущейся и закрепленной частиц; m ¾ масса движущейся частицы; x и y - координаты движущейся частицы; v x , vy- величины проекций скорости v движущейся частицы.на горизонтальную и вертикальную оси;
= 0,85 . 10-12 ф/м ¾ электрическая постоянная. Знак “-” в двух последних уравнениях соответствует разноименно заряженным частицам; в случае одноименных зарядов он меняется на “+”. Здесь q и Q ¾ соответственно заряды движущейся и закрепленной частиц; m ¾ масса движущейся частицы; x и y - координаты движущейся частицы; v x , vy- величины проекций скорости v движущейся частицы.на горизонтальную и вертикальную оси;
Метод Эйлера решения обыкновенных дифференциальных уравнений. Рассмотрим задачу Коши: Найти решение 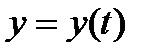 дифференциального уравнения
дифференциального уравнения 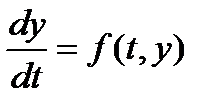 для
для  при начальном условии
при начальном условии 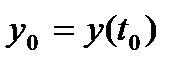 . Для численного решения уравнения проведем дискретизацию следующим простейшим способом: заменим непрерывные промежутки изменения t и y дискретными множествами значений, непрерывные функции –дискретными, производную – конечноразностным отношением. Получим :
. Для численного решения уравнения проведем дискретизацию следующим простейшим способом: заменим непрерывные промежутки изменения t и y дискретными множествами значений, непрерывные функции –дискретными, производную – конечноразностным отношением. Получим : 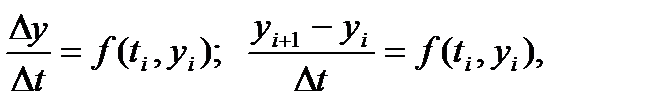 откуда получаем разностную схему Эйлера:
откуда получаем разностную схему Эйлера:
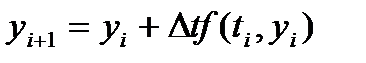 (9)
(9)
Здесь отрезок 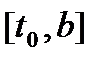 разбит на n равных частей длиной
разбит на n равных частей длиной 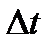 , так что
, так что 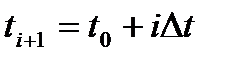 .
.
Вопрос о выборе конкретного значения 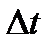 весьма непрост и определяется следующими соображениями. При компьютерном моделировании можно получить решение задачи о движении тела на некотором дискретном множестве значений t0, t0+ Dt, …, t0+(n-1)Dt. Чем больше величина Dt, тем меньшая точность в передаче значений непрерывных функций их дискретными представлениями. Однако, уменьшение шага Dt не всегда ведет к улучшению результатов моделирования. Одна из причин заключается в том, что чем меньше шаг, тем больше арифметических действий, ведущих к увеличению глобальной погрешности округления. Более эффективными при моделировании процессов, описываемых дифференциальными уравнениями, являются методы Эйлера-Коши или Рунге-Кутта более высокого порядка аппроксимации, чем метод Эйлера.
весьма непрост и определяется следующими соображениями. При компьютерном моделировании можно получить решение задачи о движении тела на некотором дискретном множестве значений t0, t0+ Dt, …, t0+(n-1)Dt. Чем больше величина Dt, тем меньшая точность в передаче значений непрерывных функций их дискретными представлениями. Однако, уменьшение шага Dt не всегда ведет к улучшению результатов моделирования. Одна из причин заключается в том, что чем меньше шаг, тем больше арифметических действий, ведущих к увеличению глобальной погрешности округления. Более эффективными при моделировании процессов, описываемых дифференциальными уравнениями, являются методы Эйлера-Коши или Рунге-Кутта более высокого порядка аппроксимации, чем метод Эйлера.
