Лекция 15. Бесконечно малые функции

Определение. Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .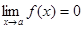

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f(x) = A + a(x), где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).

Свойства бесконечно малых функций:

1. Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2. Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3. Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4. Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Бесконечно большие функции и их связь с бесконечно малыми

Определение. Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число d>0, что неравенство ïf(x)ï>M выполняется при всех х, удовлетворяющих условию 0 < ïx - aï < d.

Записывается .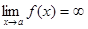

Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим: 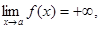а если заменить на f(x)<M, то: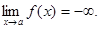

Определение. Функция называется бесконечно большойпри х®а, где а – число или одна из величин ¥, +¥ или -¥, если 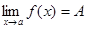, где А – число или одна из величин ¥, +¥ или -¥.

Теорема. Если f(x)®0 при х®а (если х®¥ ) и не обращается в ноль, то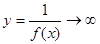

Сравнение бесконечно малых функций

Пусть a(х), b(х) и g(х) – бесконечно малые функции при

х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.

Например, функция f(x) = x¹⁰ стремится к нулю быстрее, чем функция f(x) = x.

Определение. Если 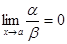, то функция a называется бесконечно малой более высокого порядка, чем функция b.

Определение. Если 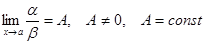, то a и b называются бесконечно малыми одного порядка.

Определение. Если 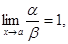то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.

Определение. Бесконечно малая функция a называется бесконечно малой порядка kотносительно бесконечно малой функции b, если предел 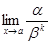конечен и отличен от нуля.

Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 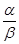не имеет предела, то функции несравнимы.