Основные законы распределения случайных величин в теории надежности
Случайные величины, с помощью которых определяются показатели надежности могут быть полностью определены, если известна функция плотности распределения. В свою очередь, функция плотности определяется на основе экспериментальных данных.
При этом возможны два подхода в исследовании:
- если необходимо выявить имеющиеся в действительности закономерности работы аппаратуры для принятия мер по повышению ее надежности, то необходимо иметь дело непосредственно с экспериментальными данными;
- при теоретических исследованиях различных аспектов надежности применяются известные теоретические распределения, которые определяются путем аппроксимации данных полученных экспериментально.
В настоящее время в теории надежности наиболее широкое распространение получили следующие законы распределения случайных величин: экспоненциальный, Релея, гамма, Вейбулла, нормальный, логарифмически-нормальный.
Экспоненциальный закон распределения
Этому закону подчиняются случайные величины, на которые оказывают влияние большое число факторов, среди которых есть доминирующий. Экспоненциальное распределение является распределением времени между событиями, появляющимися с постоянной интенсивностью. В теории надежности экспоненциальное распределение применяется для описания наработки сложных систем, прошедших период приработки.
Экспоненциальный закон очень популярен в теории надежности. Это объясняется тем, что экспоненциальный закон физически очень естественен, прост и удобен для использования. Почти все задачи, возникающие в теории надежности для этого закона распределения, оказываются на порядок проще, чем для других видов законов распределения.
Для экспоненциального закона имеем следующие зависимости:
 (1.11)
(1.11)
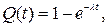 (1.12)
(1.12)
 (1.13)
(1.13)
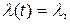 (1.14)
(1.14)
 (1.15)
(1.15)
где  - параметр распределения.
- параметр распределения.
Графики, характеризующие экспоненциальное распределение, показаны на рис. 2 а.
Закон распределения Релея
Данное распределение встречается при анализе надежности автоматизированных систем и технических процессов с резервированием элементов, узлов и технологического оборудования. Закон Релея может применяться с другими законами распределения при исследовании надежности аппаратуры, имеющей элементы с выраженным эффектом старения.
Основные характеристики имеют следующий вид:
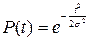 , (1.16)
, (1.16)
 , (1.17)
, (1.17)
 , (1.18)
, (1.18)
 , (1.19)
, (1.19)
 (1.20)
(1.20)
Графики, характеризующие распределение Релея, показаны на рис. 2 б.
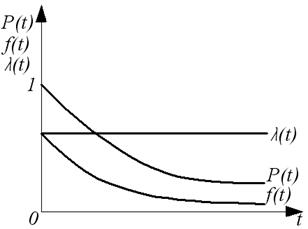
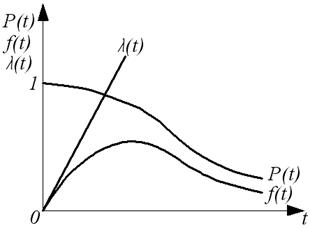
A) б)
Р и с. 2. Графики изменения показателей надежности
а- экспоненциальное распределение, б – распределение Релея
