Расчеты на устойчивость по коэффициенту снижения допускаемого напряжения на сжатие

Вместо двух формул (Эйлера и Ясинского), каждая из которых пригодна для определенного диапазона гибкостей, удобнее иметь одну формулу, которой можно пользоваться при любой гибкости стержня.

Эта практическая формула, широко применяющаяся при расчете строительных конструкций, имеет следующий вид:

,

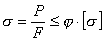(13.19)

где [σ] - основное допускаемое напряжение на сжатие; φ - коэффициент снижения основного допускаемого напряжения (или коэффициент продольного изгиба); F - площадь поперечного сечения стержня.

Величина φ зависит от материала и гибкости стержня. Его значения приведены в таблице 13.1.

Величина φ[σ] может рассматриваться как допускаемое напряжение при расчете на устойчивость, т. е.

.

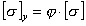(13.20)

Таблица 13.1.

Гибкость, λ	φ для
сталей Ст 1,2,З,4	стали Ст5	стали повышенного качества ?σпц>320 МПа	чугуна	дерева
	1.00	1.00	1.00	1.00	1.00
	0.99	0.98	0.97	0.97	0.99
	0.96	0.95	0.95	0.91	0.97
	0.94	0.92	0.91	0.81	0.93
	0.92	0.89	0.87	0.69	0.87
	0.89	0.86	0.83	0.57	0.80
	0.86	0.82	0.79	0.44	0.71
	0.81	0.76	0.72	0.34	0.60
	0.75	0.70	0.65	0.26	0.48
	0.69	0.62	0.55	0.20	0.38
	0.60	0.51	0.43	0.16	0.31
	0.52	0.43	0.35	-	0.25
	0.45	0.37	0.30	-	0.22
	0.40	0.33	0.26	-	0.18
	0.36	0.29	0.23	-	0.16
	0.32	0.26	0.21	-	0.14
	0.29	0.24	0.19	-	0.12
	0.26	0.21	0.17	-	0.11
	0.23	0.19	0.15	-	0.10
	0.21	0.17	0.14	-	0.09
	0.19	0.16	0.13	-	0.08

Для подбора сечения формулу (13.19) приводят к следующему виду:

.

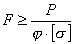При этом значением φ приходится задаваться, так как гибкость λ неизвестна, ибо неизвестна площадь сечения F, а гибкость зависит от нее. В качестве первого приближения рекомендуется принимать φ₁=0,5. Затем определяют величины F, I_min, i_min, λ и по таблице 13.1 находят соответствующее значение φ₁.

Если получается большая разница между значениями φ₁ и φ₂, то следует повторить расчет, задавшись новым значением φ₂:

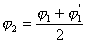
и т. д., пока разница между последовательными значениями не будет превышать 4-6%.

Для стержней, сечения которых имеют значительные ослабления (например, от отверстий), кроме расчета на устойчивость должен производиться и обычный расчет на прочность по формуле

,

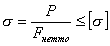где F - рабочая (нетто) площадь сечения стержня.

При расчете же на устойчивость берется полная площадь сечения F_брутто.

В некоторых случаях (например, при расчете элементов машиностроительных конструкций) значения коэффициентов запаса устойчивости, предусмотренные при составлении таблиц коэффициентов φ (n_y≈1.8), недостаточны. В этих случаях расчет следует вести, исходя непосредственно из требуемого коэффициента n_y и пользуясь формулой Эйлера или Ясинского. Так же следует поступать при расчете на устойчивость стержней из материалов, которые не отражены в таблице коэффициентов φ.