Кусочно-постоянная интерполяция

Министерство образования и науки РФ

ФГБОУ ВПО «Кубанский государственный технологический

Университет»

Кафедра электротехники и электрических машин

УТВЕРЖДАЮ
Заведующий кафедрой электротехники и электрических машин
к.т.н., доцент		ЯЯ.М. Кашин
____ _______ 2015 г.

Конспект лекций

По дисциплине «Численные методы расчета

Электрооборудования»

для студентов направления 13.04.02 «Электроэнергетика и электротехника»

Квалификация выпускника – магистр

Разработал:

к.т.н., доц. И.Н. Автайкин

Обсужден на заседании кафедры

электротехники и электрических машин

25 августа 2015 г. (протокол № 1)

Секретарь кафедры

к.т.н., доц. С.А. Попов

2015 г.

Лекция № 2 (2 часа)

По дисциплине «Численные методы расчета электрооборудования»

Тема № 1. Интерполирование

Цели: 1. Формирование следующих компетенций:

ОПК-2: Способностью применять современные методы исследования, оценивать и представлять результаты выполненной работы.

.

2. Формирование уровня обученности:

Знать: основные математические методы исследования электрооборудования.

Уметь: оценивать и анализировать результаты исследования.

Владеть: современными методами и математическими алгоритмами исследования электрооборудования.

Материальное обеспечение:

Учебные вопросы

Введение

1. Кусочно-постоянная интерполяция.

2. Кусочно-линейная интерполяция.

3. Кубический интерполяционный сплайн.

4. Многочлен Лагранжа.

Литература

1. Бахвалов Н.С., Жидков Н.П. Кобельков Г.М. Численные методы / Учебн. пособие- М.: Наука, 2011.- 631с.

2. Марчук Г.И. Методы вычислительной математики / Учебн. пособие- М.: Наука, 2011.- 535с.

Интерполирование

Введение

Аппроксимировать – это означает "приближённо заменять".

Допустим, известны значения некоторой функции в заданных точках. Требуется найти промежуточные значения этой функции. Это так называемая задача о восстановлении функции. Кроме того, при проведении расчетов сложные функции удобно заменять алгебраическими многочленами или другими элементарными функциями, которые достаточно просто вычисляются (задача о приближении функции).

Постановка задачи интерполяции

На интервале [a, b] заданы точки x_i, i=0, 1,..., N; a ≤ x _i ≤ b, и значения неизвестной функции в этих точках f_i, i=0, 1,...., N. Требуется найти функцию F(x), принимающую в точках x_i те же значения f_i

Точки 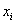называются узлами интерполяции, а условия F(x_i)= f_i. – условиями интерполяции. При этом F(x) ищем только на отрезке [a,b]. Если необходимо найти функцию вне отрезка, то - это задача экстраполяции. Пока мы будем рассматривать только интерполяционные задачи.

Задача имеет много решений, т.к. через заданные точки (x_i, f_i), i=0, 1,..., N, можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай аппроксимации функции многочленами, т.е. .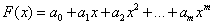

Все методы интерполяции можно разделить на локальные и глобальные. В случае локальной интерполяции на каждом интервале [x_i–1, x_i] строится отдельный полином. В случае глобальной интерполяции отыскивается единый полином на всем интервале [a, b]. При этом искомый полином называется интерполяционным полиномом.

Кусочно-постоянная интерполяция

Кусочно-постоянная интерполяция используется нами повседневно, когда мы говорим, сколько сейчас времени: в течение, например, минуты время считается постоянным (12 часов 27 минут). Графическое представление такой интерполяции приведено на рис. 1.

Рис. 1

Кусочно-постоянная интерполяция самая простая, но и обладает самыми примитивными качествами с точки зрения применения в моделировании. Действительно: в каждом узле полученная интерполяционная функция терпит разрыв, а разрывная функция применима далеко не во всех задачах.

На каждом отрезке интерполяционный многочлен равен константе, а именно левому или правому значению функции.

Для левой кусочно-линейной интерполяции 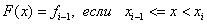, т.е.

Для правой кусочно-линейной интерполяции 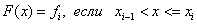, т.е.

Легко понять, что условия интерполяция выполняются. Построенная функция является разрывной), что ограничивает ее применение. Для левой кусочно-линейной интерполяции имеем графическое представление:

Рис. 2