Передаточные функции САУ

Передаточная функция - функция, связывающая один входной и один выходной сигналы САУ. Является формой записи системы ДУ САУ решённой относительно требуемой выходной координаты. Обычно ПФ записывается не для временного домена, а для домена Лапласа, связывая в этом варианте не сигналы (т.е. не функции времени), а их изображения.

ПФ-ии получают из ДУ решенного относительно требуемой координаты системы (уравнение (4) или (5)). Для чего правую часть уравнения делят на характеристический полином D(p). Отношения полиномов в правой части при возмущающих воздействиях и есть ПФ-ии.

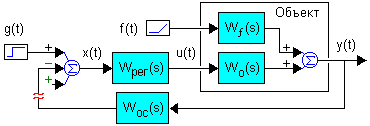
Для типовой структурной схемы замкнутой САУ различают 3 основные ПФ, применяемые для исследований:

1. W(p) = y(p)/x(p) × W_ос(p) = W_рег(p) W_о(p) W_ос(p) - ПФ разомкнутой системы;
2. F(p) = y(p)/g(p) - ПФ замкнутой системы;
3. F_x(p) = x(p)/g(p) - ПФ замкнутой системы по ошибке.

Запишем по структурной схеме уравнение движения для разомкнутой системы:

.

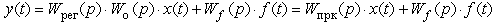где: W_прк(p) - ПФ прямого канала системы.

Замкнем систему с помощью уравнения замыкания:

.

Тогда совместное решение даст уравнение движения замкнутой системы:

и уравнение ошибки замкнутой системы:

.

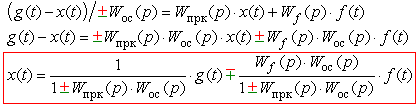При отсутствии помехи f (t) выходная величина связана с задающим воздействием ПФ замкнутой системы:

.

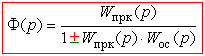А ошибка - с задающим воздействием ПФ замкнутой системы по ошибке:

.

При этом:

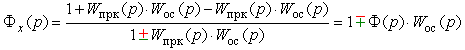
Другие связывающие отношения

Разделим уравнение движения (4) на уравнение ошибки (5), считая, что f(t)=0 и W_ос(p)=1:

y(t) / x(t) = R(p) / Q(p) , => W(p) = R(p) / Q(p) .

В соответствии с теми же уравнениями и уравнением замыкания характеристический полином D(p) = R(p) + Q(p). Добавим 1 к W(p):

1 + W(p) = Q(p) / Q(p) + R(p) / Q(p) = D(p) / Q(p) .

При исследованиях характеристический полином приравнивают к нулю, т.е. вместо него можно использовать W(p):

1 + W(p) = 0 , - характеристическое уравнение.

А так же:

W(p) = [D(p) - Q(p)] / Q(p) = D(p)/Q(p) - 1 = R(p) / [D(p) - R(p)] .

и

W(p) = F(p) / [1 - F(p)] , W(p) = [1 - F_x(p)] / F_x(p) .

Линеаризация ДУ САР

Достаточно часто встречаются звенья, имеющие нелинейную зависимость между входной и выходной координатами. Если для малых отклонений от установившегося режима нелинейность несущественна, то в этом случае до составления исходных ДУ САУ (1), ..., (5) выполняют процедуру линеаризации.

Суть линеаризации

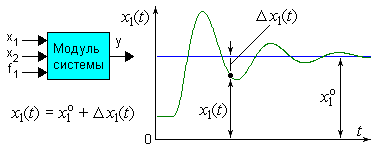
1. Пусть нелинейное динамическое уравнение звена имеет вид:

F(x₁, x₂, x₂', y, y', y'', y''') = j( f, f ') .

1. Тогда уравнение установившегося состояния, всилу равенства нулю всех производных, имеет вид:

F^o(x₁^o, x₂^o, 0, y^o, 0, 0, 0) = j( f ^o, 0) .

1. Перейдем к уравнению динамики для отклонений, выполнив подстановки:

x₁ = x₁^o+Dx₁(t), x₂ = x₂^o+Dx₂(t), x₂' = Dx₂'(t),

y = y^o+Dy(t), y' = Dy'(t), y'' = Dy''(t), y''' = Dy'''(t);

и разложив функцию F в ряд:

.

1. Завершая линеаризацию, вычтем из левой и правой части уравнение установившегося состояния:

(*).