Часть I. Кратные интегралы

Интегральное исчисление

функции многих переменных

Ростов – на – Дону

Печатается по решению кафедры математики, алгебры и математического анализа педагогического института «Южного федерального университета».

Составители: Смелик Г.Г., доцент

Белик Е.В., доцент

Рецензент: Полисмаков А.И., доцент

Основное назначение настоящих методических рекомендаций – оказать помощь студенту – заочнику в самостоятельной работе по разделу «Интегральное исчисление функции многих переменных» при выполнении контрольной работы.

В издании приводится минимум сведений из теории кратных и криволинейных интегралов, даны решения типовых задач, подобные которым предлагаются во всех вариантах контрольной работы, а также на экзамене по данному разделу математического анализа.

© Смелик Г.Г., Белик Е.В., 2012.

В в е д е н и е

«Интегральное исчисление функции многих переменных» – важный раздел дисциплины «Математический анализ» основной образовательной программы подготовки выпускника ВУЗа по специальности 032 100 Математика (стандарт 2005 г.). По учебному плану на заочном отделении педагогического института Южного федерального университета на изучение этого раздела математического анализа в зимнюю сессию отводится всего 22 часа аудиторных занятий: 12 часов лекций и 10 часов практических занятий. В межсессионный период предусматривается выполнение контрольной работы, а в летнюю сессию – экзамен.

Настоящее пособие имеет в основном практический характер. Оно окажет помощь студенту-заочнику при выполнении контрольной работы, а также даст ему возможность подготовиться к сдаче экзамена. По теоретической части раздела «Интегральное исчисление функции многих переменных» в пособии даны лишь краткие теоретические справки, поэтому для подготовки к экзамену необходимо также использовать один из следующих учебников:

1. Бохан К.А. и др. Курс математического анализа. – М.: Просвещение, 1972, т. 2.

2. Кудрявцев Л.Д. Курс математического анализа. – М.: Высшая школа, 1981, т. 2.

3. Фихтенгольц Г.М. Основы математического анализа. – М.: Наука, 1968, т. 2

4. Виленкин Н.Я. и др. Задачник по курсу математического анализа. – М.: Просвещение, 1971, ч. 2.

и другие.

Чтобы помочь студенту-заочнику ориентироваться в обширном материале литературных источников, приведем список примерных вопросов, включенных в экзаменационные билеты.

1. Задача об объёме цилиндрического бруса.
2. Понятие двойного интеграла.
3. Геометрический смысл двойного интеграла.
4. Условия существования двойного интеграла.
5. Свойства двойных интегралов и интегрируемых функций.
6. Вычисление двойных интегралов. Случай прямоугольной области.
7. Вычисление двойных интегралов. Случай произвольной области.
8. Криволинейные координаты. Отображение плоских областей.
9. Замена переменных в двойном интеграле (полярные координаты). Якобиан.
10. Площадь поверхности (цилиндр Шварца).
11. Механические и физические приложения двойного интеграла.
12. Понятие тройного интеграла.
13. Вычисление тройных интегралов.
14. Свойства тройных интегралов.
15. Замена переменных в тройном интеграле. Цилиндрические координаты.
16. Замена переменных в тройном интеграле. Сферические координаты.
17. Приложения тройных интегралов.
18. Криволинейные интегралы 1-го типа.
19. Вычисление криволинейных интегралов 1-го типа.
20. Криволинейные интегралы 2-го типа.
21. Вычисление криволинейных интегралов 2-го типа.
22. Свойства криволинейных интегралов 2-го типа.
23. Формула Грина-Остроградского.
24. Независимость криволинейного интеграла от пути интегрирования.
25. Приложения криволинейных интегралов.

Часть I. Кратные интегралы

1.1. Двойные интегралы

Дадим в развернутом виде общее определение двойного интеграла.

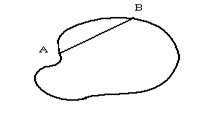Рис. 1

Рассмотрим криволинейную замкнутую область (D). Отрезок, соединяющий две точки контура, ограничивающего данную область, называется хордой этого контура (рис. 1). Наибольшая из хорд данной замкнутой области (D) называется диаметром этой области.

Пусть в замкнутой квадрируемой области (D) определена некоторая функция z = f(x,y). Разобьем область (D) произвольным образом сетью кривых на конечное число частичных областей (D₁), (D₂), (D₃),…,(D_n), площади которых соответственно обозначим через D₁, D₂, D₃,…,D_n. В каждой частичной области (D_i) возьмем произвольную точку ( 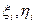) и составим сумму

,

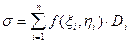которую будем называть интегральной суммой для функции z = f(x,y) в области (D). Обозначим через λ наибольший из диаметров частичных областей (D_i).