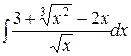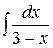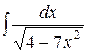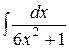Первообразная для функции и неопределенный интеграл от нее
Лекция 35. Понятие неопределенного интеграла. Свойства неопределенного интеграла. Правила интегрирования. Таблица интегралов. Непосредственное интегрирование.
Интегральное исчисление, наряду с дифференциальным исчислением, принадлежит к числу важнейших составляющих высшей математики (вместе они составляют так называемый математический анализ). Это исчисление базируется на понятиях неопределенного и определенного интегралов, введенных в математику Ньютоном и Лейбницем в конце 17-го века параллельно с введением ими же понятий производных и дифференциалов функций.
Первообразная для функции и неопределенный интеграл от нее.
В дифференциальном исчислении ставилась задача: для данной функции найти ее производную. В интегральном исчислении ставится обратная задача: по производной функции найти саму функцию.
Пусть y = f(x) – некоторая заданная функция.
Определение. Всякая функция y=F(x), производная  которой совпадает с функцией y = f(x) , называется первообразной для функции y = f(x). То есть если
которой совпадает с функцией y = f(x) , называется первообразной для функции y = f(x). То есть если 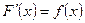 , то функция
, то функция  будет первообразной для функции f(x) (а f(x) будетпроизводной от своей первообразной F(x)).
будет первообразной для функции f(x) (а f(x) будетпроизводной от своей первообразной F(x)).
Пример1. Функция  является первообразной для функции
является первообразной для функции  , так как
, так как  .
.
Отметим, что функция  - не единственная первообразная для функции
- не единственная первообразная для функции  . В самом деле, любая функция вида
. В самом деле, любая функция вида  + С, где С – произвольная (неопределенная) константа, тоже будет первообразной для функции
+ С, где С – произвольная (неопределенная) константа, тоже будет первообразной для функции  . Действительно,
. Действительно,  .
.
И вообще, если F(x) – первообразная для заданной функции f(x), то и все функции вида F(x)+C, где С - неопределенная константа, тоже будут первообразными для функции f(x). Действительно, если 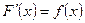 , то и
, то и 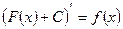 .
.
Таким образом, найдя какую-либо первообразную F(x) для данной функции f(x), мы сразу можем записать для нее и множество других первообразных:
F(x) + C (С - неопределенная константа) (1)
Более того, мы сейчас докажем, что выражение (1) дает множество всех первообразных для функции f(x).
Действительно, пусть F(x) – какая-либо конкретная первообразная для функции f(x), а  – любая другая первообразная для этой же функции f(x). Образуем новую функцию
– любая другая первообразная для этой же функции f(x). Образуем новую функцию 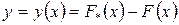 и найдем ее производную:
и найдем ее производную:

Как оказалось, эта функция 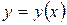 имеет нулевую производную для любого
имеет нулевую производную для любого 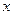 . Но, как известно, производная функции характеризует скорость изменения функции. Значит, скорость изменения функции
. Но, как известно, производная функции характеризует скорость изменения функции. Значит, скорость изменения функции 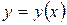 для любого х равна нулю. А это значит, что при изменении х функция
для любого х равна нулю. А это значит, что при изменении х функция 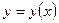 не меняется (сохраняет постоянное значение).То есть
не меняется (сохраняет постоянное значение).То есть  , где С - некоторая постоянная. Таким образом,
, где С - некоторая постоянная. Таким образом,  , откуда
, откуда  . То есть действительно любая первообразная
. То есть действительно любая первообразная  для функции
для функции 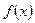 находится среди функций (1). Иначе говоря, множество функций (1) действительно представляет собой множество всех первообразных для функций
находится среди функций (1). Иначе говоря, множество функций (1) действительно представляет собой множество всех первообразных для функций 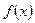 . то множество Лейбниц обозначил специальным символом
. то множество Лейбниц обозначил специальным символом
 (2)
(2)
и назвал неопределенным интегралом от функции 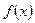 . Здесь знак
. Здесь знак 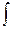 - знак неопределенного интеграла;
- знак неопределенного интеграла; 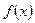 - подынтегральная функция;
- подынтегральная функция; 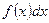 - подынтегральное выражение;
- подынтегральное выражение; 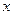 - переменная интегрирования.
- переменная интегрирования.
Так как выражение (2) - это лишь другое обозначение выражения (1), то можно записать:
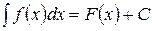 (3)
(3)
Таким образом, отыскивая (вычисляя) неопределенный интеграл 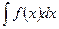 , мы тем самым ищем все первообразные
, мы тем самым ищем все первообразные  для подынтегральной функции
для подынтегральной функции  . То есть ищем все функции, производные от которых равны
. То есть ищем все функции, производные от которых равны 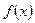 . Эти функции (их бесчисленное множество) представляют собой сумму конкретной функции
. Эти функции (их бесчисленное множество) представляют собой сумму конкретной функции  (конкретной первообразной для
(конкретной первообразной для 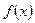 ) и неопределенной константы С, которой можно придать любое значение. Из-за наличия этой неопределенной константыв равенстве (3) и результат вычисления неопределенного интеграла оказывается неопределенным. Отсюда и термин: неопределенный интеграл.
) и неопределенной константы С, которой можно придать любое значение. Из-за наличия этой неопределенной константыв равенстве (3) и результат вычисления неопределенного интеграла оказывается неопределенным. Отсюда и термин: неопределенный интеграл.
Если неопределенный интеграл 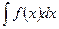 найден верно (то есть множество всех первообразных
найден верно (то есть множество всех первообразных  для функции
для функции 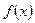 найдено верно), то должно выполняться проверочное для (3) равенство:
найдено верно), то должно выполняться проверочное для (3) равенство:
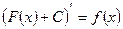 (4)
(4)
Пример 2.
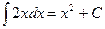 - верно, так как
- верно, так как 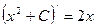 .
.
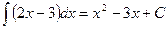 - верно, так как
- верно, так как  .
.
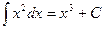 - неверно, так как
- неверно, так как 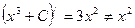 .
.
Основные свойства неопределенных интегралов.
1. Свойство 1.Производная от неопределенного интеграла равна подынтегральной функции:
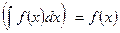 (5)
(5)
Доказательство. Используя (3) и (4), получим:

2. Свойство 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
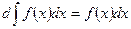 (6)
(6)
Доказательство. Вспоминая формулу для нахождения дифференциала функции, получим:
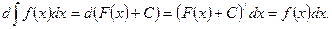
3. Свойство 3. Неопределенный интеграл от дифференциала функции равен этой функции плюс неопределенная константа:
 (7)
(7)
Доказательство:
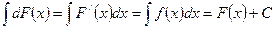 .
.
4. Свойство 4. Нахождение функции  по ее дифференциалу
по ее дифференциалу 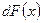 : если
: если  , то
, то
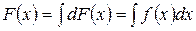 . (8)
. (8)
Доказательство. Если  , то
, то 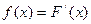 . А это значит, что функция
. А это значит, что функция  является первообразной для функции
является первообразной для функции 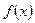 . Но этих первообразных для функции
. Но этих первообразных для функции 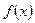 имеется бесчисленное количество, и все они находятся посредством вычисления
имеется бесчисленное количество, и все они находятся посредством вычисления 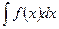 .
.
Примечание. Функция  определяется по формуле (8) неоднозначно – она определяется с точностью до неопределенной константы С, которая появится после вычисления
определяется по формуле (8) неоднозначно – она определяется с точностью до неопределенной константы С, которая появится после вычисления 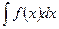 . Поэтому для однозначного определения функции
. Поэтому для однозначного определения функции  по ее дифференциалу
по ее дифференциалу  нужно задать некоторое дополнительное условие для этой функции. Таким условием, в частности, может быть следующее условие:
нужно задать некоторое дополнительное условие для этой функции. Таким условием, в частности, может быть следующее условие:  , где
, где  и А - заданные числа.
и А - заданные числа.
Пример 3. Найти функцию  , если известно, что
, если известно, что  и что
и что 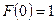 .
.
Решение. Используя (8), получаем:
 .
.
Мы получили бесчисленное множество функций  :
:
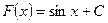 (С - неопределенная константа).
(С - неопределенная константа).
Константу С найдем из дополнительного условия  :
:
 .
.
Таким образом, получаем окончательно: 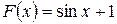 .
.
5. Свойство 5. Постоянный множитель можно выносить за знак неопределенного интеграла:
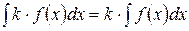 (k – константа, k
(k – константа, k 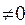 ) (9)
) (9)
Доказательство. Рассмотрим правую часть равенства (9):
 ,
,
где 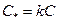 - неопределенная константа (если k
- неопределенная константа (если k 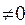 ). Таким образом, равенство (9) принимает вид:
). Таким образом, равенство (9) принимает вид:
 .
.
А это равенство верно, что подтверждает его проверка:
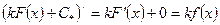
6. Свойство 6. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций:
 (10)
(10)
Доказательство. Вычисляя правую часть равенства (10), получаем:
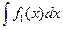


 …
… 
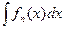 = =
= = 
= 
где
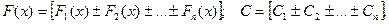 .
.
Таким образом, доказываемое равенство (10) принимает вид:
 = F(x) + C
= F(x) + C
И оно верно, так как
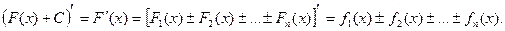
При вычислении неопределенных интегралов бывает полезно использовать следующие правила:
1. Если 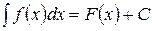 , то
, то
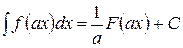 . (11)
. (11)
Действительно, дифференцируя левую и правую части равенства (11), получим:

 .
.
Производные от правой и левой частей равны, что и требовалось доказать.
2. Если 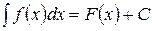 , то
, то
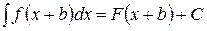 . (12)
. (12)
3. Если 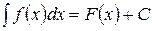 , то
, то
 . (13)
. (13)
Равенства (12) и (13) доказываются дифференцированием правой и левой частей равенств.
Пример 4. 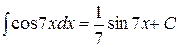 ( по формуле 11).
( по формуле 11).
Пример 5. 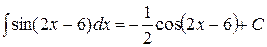 ( по формуле 13).
( по формуле 13).
Таблица основных неопределенных интервалов.
1.  8.
8.  =
= 
2.  =
= 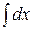 =x+C 9.
=x+C 9.  = -
= - 
3.  =
=  +C (n
+C (n 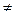 -1) 10.
-1) 10. 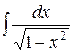 =
= 
4.  =
= 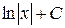 11.
11. 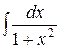 =
=  (14)
(14)
5.  =
=  +C 12.
+C 12. 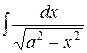 =
=  +C
+C
5*. 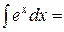 ex+C 13.
ex+C 13.  =
= 
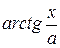 +C
+C
6. 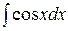 =
= 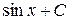 14.
14.  =
=  +C
+C
7. 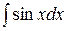 = -
= -  15.
15.  =
= 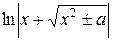 +C
+C
Используя проверку (4) для неопределенного интеграла (3), легко убедиться в истинности каждого из результатов таблицы (14). Проверим, например, первые четыре неопределенные интеграла.
1) 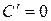 – верно;
– верно;
2)  - верно;
- верно;
3)  =
= 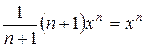 - верно;
- верно;
4а) Если  то
то 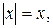 и (4) принимает вид:
и (4) принимает вид:  . А это верно, так как
. А это верно, так как 
4б) Если 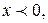 то
то  , и (4) принимает вид:
, и (4) принимает вид:  . А это верно, так как
. А это верно, так как 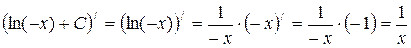 .
.
Совершенно аналогично дифференцированием правой части можно подтвердить и все остальные равенства в таблице (14).
Пример 5. Найти неопределенный интеграл:  .
.
Решение. Разделив числитель подынтегральной функции на знаменатель и использовав второе и третье правила интегрирования, а также таблицу основных неопределенных интегралов, получим:

Пример 5. Найти неопределенный интеграл: 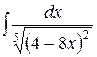 .
.
Решение.
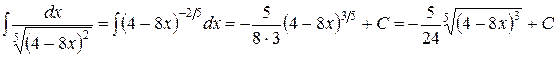
Таблица (14) содержит лишь наиболее простые неопределенные интегралы. Но в математических справочниках содержатся многие сотни (и даже тысячи) наиболее часто встречающихся на практике неопределенных интегралов. К таким справочникам относятся, например, следующие:
1.Бронштейн И.Н. и Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. М., «Наука», 1981.
2.Двайт Г.Б. Таблицы интегралов и другие математические формулы. М. «Наука», 1977.
3.Градштейн И.С. и Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М., «Наука», 1971.
Таким образом, если требуется вычислить некоторый неопределенный интеграл, то его можно просто поискать в справочнике. Если же нужного интеграла в справочнике нет, то этот интеграл, так или иначе, стараются свести к одному или нескольким табличным интегралам. О методах такого сведения мы поговорим в следующем параграфе.
А сейчас пока лишь отметим следующее важное обстоятельство, связанное с интегрированием функций (с вычислением неопределенных интегралов) и отличающее интегрирование от дифференцирования. Производная  любой элементарной функции
любой элементарной функции 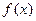 всегда может быть найдена, и она опять же элементарная функция. А вот неопределенный интеграл
всегда может быть найдена, и она опять же элементарная функция. А вот неопределенный интеграл  не от всякой элементарной функции
не от всякой элементарной функции 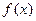 может быть записан через элементарные функции вида F(x)+C . Иначе говоря, не всякий неопределенный интеграл
может быть записан через элементарные функции вида F(x)+C . Иначе говоря, не всякий неопределенный интеграл  может быть сведен к табличным. А стало быть, не всякий неопределенный интеграл может быть вычислен в явном виде. Такие, не сводимые к табличным, неопределенные интегралы называются неберущимися (ибо вычислить неопределенный интеграл – это, на математическом жаргоне, «взять» интеграл). Неберущимися являются многие, даже совсем простые на первый взгляд, неопределенные интегралы. Например, такие:
может быть сведен к табличным. А стало быть, не всякий неопределенный интеграл может быть вычислен в явном виде. Такие, не сводимые к табличным, неопределенные интегралы называются неберущимися (ибо вычислить неопределенный интеграл – это, на математическом жаргоне, «взять» интеграл). Неберущимися являются многие, даже совсем простые на первый взгляд, неопределенные интегралы. Например, такие:
1. 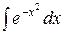 - интеграл Пуассона
- интеграл Пуассона
2. 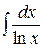 - интегральный логарифм (15)
- интегральный логарифм (15)
3.  - интегральный косинус.
- интегральный косинус.
4.  - интегральный синус.
- интегральный синус.
Эти и другие неберущиеся интегралы не могут быть найдены точно. Они могут быть найдены лишь приближенно. В соответствии с равенством (3) нахождение неопределенного интеграла сводится к нахождению какой-либо первообразной для подынтегральной функции. Вот эту первообразную для подынтегральной функции можно, используя компьютерные методы, подобрать приближенно с любой степенью точности.
Упражнения
1. Показать, что на всей числовой оси ох функция 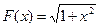 является первообразной для функции
является первообразной для функции  .
.
2. Найти все первообразные для функции 
Ответ: 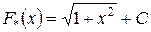 .
.
3. Верно ли равенство: 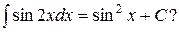
Ответ: верно.
4.Найти функцию 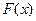 , если
, если  и
и 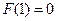 .
.
Ответ:  .
.
5) Используя основные свойства неопределенного интеграла и таблицу основных неопределенных интегралов, найти следующие интегралы: