Нагрев массивных тел. Дифференциальное уравнение теплопроводности Фурье
В отличие от тонких тел нагрев массивных характеризуется тем, что тепловая волна проникает вглубь не сразу, косвенно. Послойное включение материала в нагрев объясняется не бесконечной (как в тонких телах), а конечной скоростью распространения тела.
Время, в течение которого тепловая волна достает самого удаленного слоя материала, называется инерционным (иррегулярным). При одностороннем нагреве таким слоем является противоположная поверхность тела, а при симметричном двустороннем – его центр.
Максимальная разность Т между поверхностью и центром принято считать перепад температур  . По истечении некоторого времени наступает регулярный (упорядочный) тепловой режим, при котором различные точки подчиняются единым законам.
. По истечении некоторого времени наступает регулярный (упорядочный) тепловой режим, при котором различные точки подчиняются единым законам.
При нагреве массивного тела необходимо знать распределение величин Т в нем, или как мы сказали температурное поле, обусловленное внешним тепловым режимом.
Определение температурного поля становится возможным, если известны математические зависимости между температурой, временем и пространственными координатами в любом элементарном объеме материала. Связь между этими зависимостями устанавливается дифференциальным уравнением теплопроводности. При этом считают, что твердое тело однородно и изотропно, его теплофизические параметры и агрегатное состояние не изменяются, а также внутренние источники теплоты в нем отсутствуют.
Давайте выведем дифференциальное уравнение теплопроводности в общем, виде.
Выделим в нагревательном теле элементарный параллепипед с гранями dx, dy, dz.

В соответствии с законом сохранения энергии, разность между количеством тепла подводимого в элементарный объем за время dt и убывающего из него за то же время, равна изменению его энтальпии.
Через грань dy dz поступает количество тепла
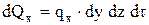 (1)
(1)
а уходит через противоположную грань
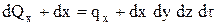 , (2)
, (2)
где qx, qx+dx – плотность потока, соответственно подводимого и отводимого в направлении оси Х.
Плотность теплового потока в этой грана находится путем разложения в ряд Тейлора
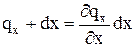
Найдем разность между количеством тепла, поступившим в параллепипед и вышедшем из него в направлении оси Х: из (1) – (2)
 ; (3)
; (3)
Аналогично определяются соответствующие величины для осей Y и Z:
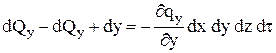 ; (4)
; (4)
 ; (5)
; (5)
Оставшееся в элементарном объеме количество тепла, расходуемое на изменение энтальпии тепла равно:
 ; (6)
; (6)
С учетом, что 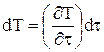 – получаем:
– получаем:
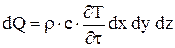 ; (7)
; (7)
Составим баланс тепла в элементарном объеме:
Уравнение (7) приравняем к уравнениям (3), (4), (5)
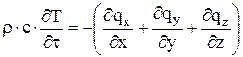 ; (8)
; (8)
Согласно закону Фурье:
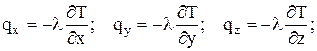
Тогда формула (8) запишется так (разделив также правую часть на r с):
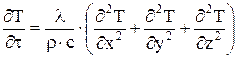 ; (9)
; (9)
Вводят оператор Лапласа Ñ2 ²набла²: 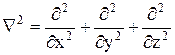 и зная, что
и зная, что 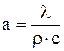 – коэффициент температуропроводности, мы получим дифференциальное уравнение теплопроводности Фурье в компактной форме:
– коэффициент температуропроводности, мы получим дифференциальное уравнение теплопроводности Фурье в компактной форме:

Коэффициент температуропроводности а м2/с, (в условиях нестационарных процессов) характеризует теплоинерционные свойства тепла. Чем больше а, тем выше скорость изменения (параметров) Т в любой точке тела и тем быстрее перестраивается его температурное поле.
Для различных веществ значение а м2/с, как и l, зависит от структуры, плотности, влажности, давления и температуры.
Таким образом, дифференциальное уравнение теплопроводности Фурье устанавливает зависимость между температурой, временем и пространственными координатами в любой элементарном объеме нагреваемого материала. Выше приведенное уравнение Фурье записано в общем виде.
Уравнение Фурье можно записать в иных системах координат. Так, для цилиндра бесконечно малой длины при симметричном относительно оси распределении температур уравнение имеет вид:
 .
.
Для тел сферической формы

где r – радиус цилиндра или шара.
При одномерных температурных полях то же уравнение для простейших форм тела имеет вид:
 ,
,
где k1 – коэффициент формы тела.
Мы отметили, что дифференциальное уравнение Фурье имеет бесконечное множество решений. Для получения единственного решения (применительно к конкретному случаю) необходимо кроме основного дифференциального уравнения Фурье задать дополнительные условия.
В условия однозначности входят:
геометрические условия, определяющие форму и размеры тела;
физические условия, т. е. физические параметры и свойства тела – l, r, Ср;
начальные условия, т. е. распределение температуры в объеме тела в некоторый момент времени, принятый за начало отсчета, t=0;
граничные условия, характеризующие тепловое взаимодействие окружающей среды с поверхностью тела, т. е. связь внешнего теплообмена в рабочем пространстве, с внутренним.
Начальное распределение температур показывает t0 состояние тела перед тем, как начался процесс нагрева и может быть различным. Наиболее простой случай имеющий практическое значение – одинаковое значение Т по всему объему: 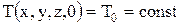 .
.
Например: это нагрев или охлаждение металла после стационарного режима.
Во многих задачах используется начальное параболическое распределение t0 по объему тела: 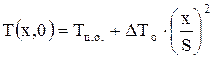
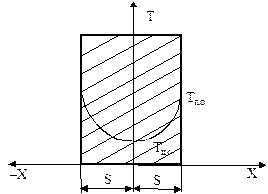
где Тц.о – температура центра в начальный момент времени;
DТ0 – нач. перепад t по сечению тела (нагрев или охлаждение предварительно разогретого металла).

Граничные условия можно задавать различными способами и на них влияет характер взаимодействия поверхности тела с окружающей средой.
1. Граничные условия первого рода (первая краевая задача).
В этом случае задается распределение t по всей поверхности тела и изменение этого распределения во времени, т. е. задается функция: Тпов.=f(х, у, z, t).
Примером граничных условий первого рода является линейное изменение t0 поверхности во времени:

где Сн – скорость нагрева.
К описанному условию можно отнести задачу разогрева кладки печи или задачу нагрева (охлаждения) тел при термообработке с заданной скоростью.
Другим примером граничных условий первого рода является постоянство температуры поверхности:
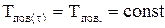
Это задачи нагрева или охлаждения с мгновенным повышением (снижением) t0пов. Тела (закалка, выдержка, томление металла).
2. Граничные условия второго рода (вторая краевая задача).
В этом случае задается распределение плотности теплового потока q по всей поверхности тела и изменение этого распределения во времени.

где n – координата, направленная к поверхности тела.
Таким образом, задание граничных условий второго рода – это задание величины градиента t0 на поверхности тела 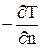 .
.
Часто принимают, что q=const – постоянный во времени и по всей поверхности тела.
Встречается в металлургических и камерных печах граничные условия третьего рода (смешанная краевая задача).
В этом случае задаются t0 окружающей среды или внешнего источника тепла Т0 и закон теплообмена между средой и поверхностью тела.
Граничные условия часто третьего рода – часто встречаются на практике.
По существу задаемся некоторая связь между известной t0 окружающей среды (внешнего источника тепла) и неизвестными t0 поверхности тела и градиентом температур на поверхности.
Например, если внешний теплообмен осуществляется путем конвективной теплоотдачи, то плотность теплового потока, подводимого к поверхности тела, выражается формулой Ньютона:
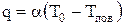
где T0 – t0 окружающей среды;
Тпов. – t0 поверхности тела.
С другой стороны плотность теплового потока на поверхности тела q может быть выражена постулатом или формулой Фурье:

где n – координата, направленная по нормам к поверхности тела.
Приравнивая правые части уравнений, на основании закона сохранения энергии, получим математическую формулировку граничных условий третьего рода:
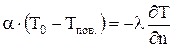 ;
;
Частный случай Т0=const или Тпеч.= const; – нагрев заготовки в печи при постоянной температуре. На практике при нагреве металла производят сочетание граничных условий нагрева. Например вначале нагрев при q.= const, а заканчивать нагрев при tпеч=.const.
Лекция 14:
