Указания по выполнению работы. Данная лабораторная работа предполагает практическое изучение метода принципа

Данная лабораторная работа предполагает практическое изучение метода принципа наложения. В ходе работы необходимо собрать схему, представленную на рисунке 4.2. Значения источников напряжений рекомендуется брать от 100-500 В, резисторов от 100 до 1 кОм. По рисунку 4.2 при помощи измерительных приборов измерить величины токов и напряжения. Для этого необходимо замерить токи:

- когда оба ключа К₁ и К₂ находятся в замкнутом положении;

- когда ключ К₁ замкнут, а ключ К₂ разомкнут;

- когда ключ К₂ замкнут, а ключ К₁ разомкнут.

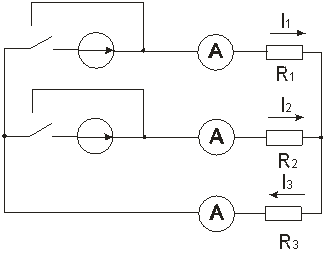
Рисунок 4.2

После измерений, по установленным значениям источника напряжения и резисторов, опираясь на теоретические сведения, необходимо:

- рассчитать значения токов производимых каждой ЭДС в отдельности;

- по рассчитанным данным найти полные токи, протекающие в схеме замещения (рис. 4.2).

Ход работы в EWB:

1) (((((((((((((((((

2) Выбираем из ряда пиктограмм Basic переключатель (ключ) . Нажав на него левой клавишей мыши, перетаскиваем его на рабочее поле EWB.

3) Перетаскиваем на рабочее поле ещё один ключ.

4) Двойным нажатием левой кнопки мыши заходим в настройки ключа и меняем клавишу срабатывания (по умолчанию ключ срабатывает на клавишу space (пробел) на “A” (рис. 4.3).

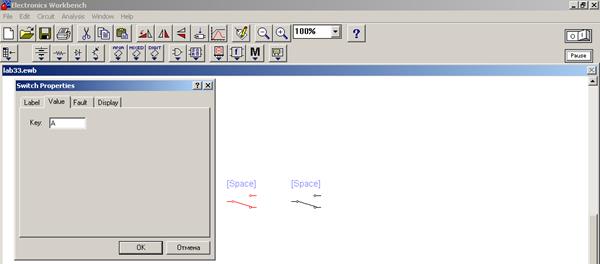
Рисунок 4.3

5) Эту процедуру повторяем для второго ключа и меняем его клавишу срабатывания на “B”(рис. 4.4).

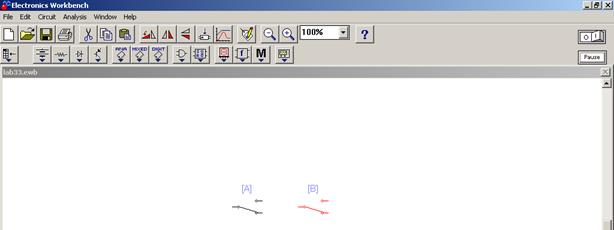
Рисунок 4.4

Теперь при нажатии клавиши “A” – срабатывает левый ключ. При нажатии “B” – правый ключ.

6) Выбираем из ряда пиктограмм нужные нам элементы, соединяем между собой и выставляем их номиналы (см. лаб. № 1, 2). Виртуальная модель электрической схемы будет иметь следующий вид (рис 4.5)

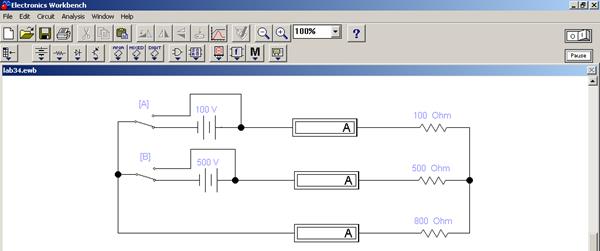
Рисунок 4.5

Контрольные вопросы

1. Сформулируйте метод принципа наложения.

2. Поясните преимущества и недостатки перед другими методами.

3. В каких схемах используется принцип наложения?

Лабораторная работа № 5

Элементы цепей переменного тока

Цель работы: понять особенности физических процессов R, L, C элементов, протекающих под воздействием переменного напряжения.

Общие сведения

Основные параметры переменного напряжения

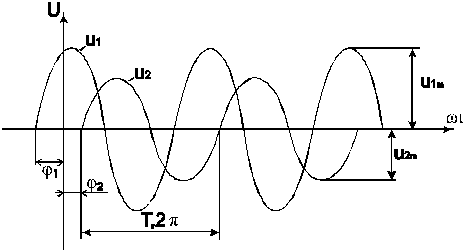
Переменное напряжение имеет синусоидальную форму (рис. 5.1). Установлено, что синусоидальная форма напряжения удобна для электротехнических расчетов, а также экономически выгодна для работы электрооборудования.

u

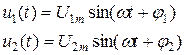
Рисунок 5.1. Графики напряжений

Основные параметры синусоидального напряжения следующие:

U_1m, U_2m –амплитудные (максимальные) значения;

φ₁ , φ₂ – начальные фазы, φ₁ – положительная, φ₂ – отрицательная;

Т – период в радианах или в секундах;

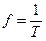- частота, Гц;

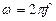- угловая частота, рад/сек.

Различают следующие значения синусоидальных величин:

U_m, Ι_m, Е_m – амплитудные значения;

U, Ι, Е – действующие значения;

u, i, e – мгновенные значения.

Действующее значение является величиной расчетной, но имеет с энергетической точки зрения глубокий физический смысл. Все приборы общего применения (вольтметры, амперметры и др.) показывают действующее значение. Математически действующее значение определяют так:

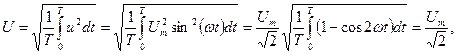
т.е.

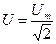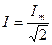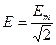, , . (5.1)

Мгновенное значение – это значение функции для какого–либо момента времени. Например, при t=0 е(0), i(0), u(0) – значение величины к этому времени.

Особенности процессов в цепях переменного напряжения

Электрический ток в проводниках неразрывно связан с магнитным и электрическим полями. При переменном токе эти поля изменяются во времени. Изменяющееся магнитное поле наводит ЭДС, изменение электрического поля сопровождается изменением зарядов на проводниках. При этом часть электромагнитной энергии превращается в тепло, часть излучается.

В реальной электрической цепи нельзя выделить какой-либо участок, с которым не были бы связаны вышеперечисленные явления. Поэтому для упрощения рассмотрения процессов электрическую цепь заменяют идеализированной цепью или расчетной схемой, составленной из идеальных элементов, в каждом из которых наблюдается только одно из перечисленных явлений.

Элементы, характеризующие преобразования электромагнитной энергии в тепло, называются активным сопротивлением r или проводимостью g.

Элементы, связанные с наличием только магнитного поля, называются индуктивностью L и взаимной индуктивностью М.

Элементы, характеризующие наличие только электрического поля, называются емкостями С. Провода, соединяющие элементы идеализированной цепи, считаются не обладающими ни R, ни L, ни С.

Резистор в цепи синусоидального тока

Пусть ток в цепи изменяется по закону 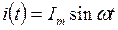. Тогда для схемы замещения (рис. 5.2) выведем законы изменения напряжения и мощности.

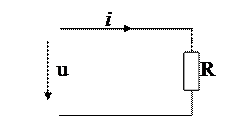
Рисунок 5.2 Резистор в цепи с синусоидальным источником напряжения

По закону Ома для мгновенных значений:

,

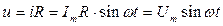где 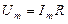- закон Ома для амплитудных значений, или

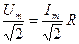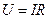, - закон Ома для действующих значений.

Закон Ома в комплексной форме будет записываться так:

.

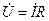Мощность цепи:

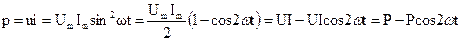, (5.2)

где 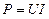- средняя мощность.

Мгновенная мощность р имеет постоянную составляющую 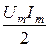и переменную 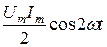с двойной частотой 2ω (рис. 5.3). При этом постоянная составляющая полностью переходит в тепловую энергию.

Векторная диаграмма цепи, содержащей только резистор (рис. 5.4).

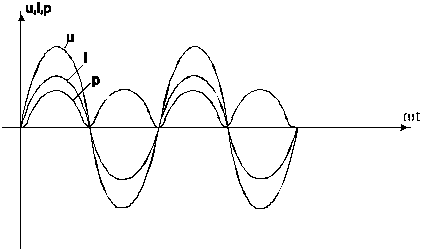
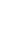
Рисунок 5.3 График тока, напряжения и мощности

Рисунок 5.4 Векторная диаграмма цепи

Идеальная катушка (индуктивность) в цепи синусоидального тока.

Пусть ток изменяется с нулевой начальной фазой. Для идеальной катушки ее резистивное сопротивление R=0. Поэтому приложенное внешнее напряжение уравновешивается только с помощью ее ЭДС самоиндукции:

, .

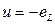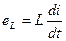Следовательно 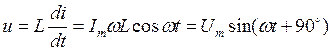, т.е. напряжение опережает ток на 90º по фазе (рис.5.5).

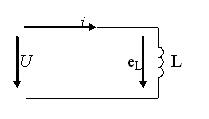
Рисунок 5.5 Индуктивность в цепи переменного тока

Здесь 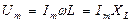- закон Ома для максимальных значений;

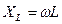- индуктивное сопротивление.

Графики тока, напряжения и мощности показаны на рисунке 5.6, а векторная диаграмма цепи показана на рисунке 5.7.

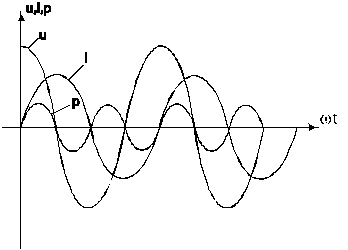
Рисунок 5.6 Графики тока, напряжения, мощности

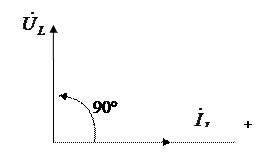
Рисунок 5.7 Векторная диаграмма

Закон Ома в комплексной форме записи будет иметь вид:

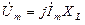или

.

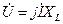Мощность цепи:

.

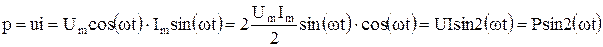Среднее значение мощности равно нулю, т.е. индуктивность не потребляет мощность. В одну четверть периода она запасает его в своем магнитном поле, а в следующую четверть периода эта энергия возвращается к источнику энергии (рис.5.8).

Конденсатор в цепи переменного тока.

Будем считать, что ток в цепи изменяется с нулевой начальной фазой .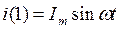

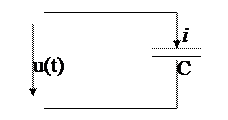
Рисунок 5.8 Конденсатор в цепи переменного тока

Ток конденсатора ,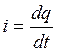

где q=СU – заряд на обкладках конденсатора. Тогда напряжение:

,

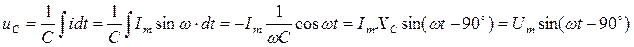т.е. напряжение на емкости отстает от тока на 90º (рис.5.9). Векторная диаграмма цепи показана на рисунке 5.10.

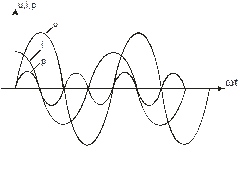
Рисунок 5.9 Графики тока, напряжения и мощности

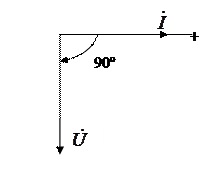
Рисунок 5.10 Векторная диаграмма цепи

В последнем выражении величина 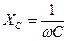- емкостное сопротивление, Ом.

Закон Ома в комплексной форме:

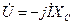. (5.3)

Мощность цепи:

.

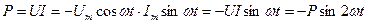Емкость также не потребляет активную мощность.

Содержание работы

1. Опытным путем определить ток, протекающий через резистор, вычислить мощность, построить векторную диаграмму тока и напряжения.

2. Опытным путем определить ток, проходящий через конденсатор, другие параметры. Вычислить мощность, построить векторную диаграмму тока и напряжения.

3. Опытным путем определить ток, проходящий через катушку индуктивности, другие параметры, вычислить мощность, построить векторную диаграмму тока и напряжения.