Экстремумы функции двух переменных. Наибольшее и наименьшее значение функции
Определение 1.Точка 
называется точкой максимума (минимума) функции 
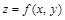, если существует такая 
–окрестность точки 
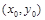, что для всех точек 
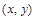из этой окрестности выполняется неравенство 
; 
.
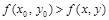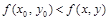Определение 2. Значение функции в точке максимума (минимума) называетсямаксимумом (минимумом) функции.
Определение 3.Точки максимума и минимума функции называются точками экстремума.
Введенные понятия носят локальный характер, так как в определении фигурируют лишь точки 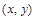довольно близкие к точке .
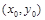Установим необходимые условия существования экстремума. Пусть 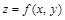дифференцируема в точке 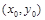и имеет в ней экстремум. Пересечем поверхность 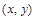плоскостью 
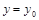. Тогда функция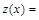 
имеет экстремум при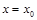 
. Учитывая необходимые условия экстремума в одномерном случае, получим:
Теорема 1. (Необходимые условия экстремума) Если в точке дифференцируемая функция 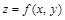имеет экстремум, то ее частные производные в это точке равны нулю:
.
Эти условия не являются достаточными.
Определение 3.Точки, в которых выполняются необходимые условия экстремума, называют стационарными.
Пример 1.Найти стационарные точки функции
.
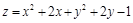Решение. Найдем частные производные и решим систему уравнений:
Стационарная точка –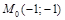 
.
Рассмотрим достаточные условия.
Теорема 2. Пусть для функции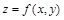 
выполняются необходимые условия экстремума в некоторой точке 
, т.е.
Пусть функция :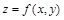
а) определена в некоторой окрестности критической точки 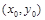, в которой 
и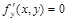 
;
б) имеет в этой точке непрерывные частные производные второго порядка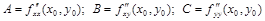 
.
Тогда: если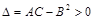 
, то в точке 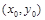функция 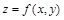имеет экстремум, причем, если 
– максимум, если 
– минимум; если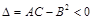 
, то функция 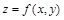экстремума не имеет.
Если 
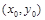, то экстремум в точке может быть, может не быть. Необходимы дополнительные исследования.
Схема исследования функции двух переменных на экстремум:
1. Найти частные производные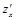 
и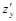 
.
2. Решить систему уравнений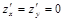 
и найти стационарные точки.
3. Найти частные производные второго порядка и вычислить значение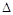 
в каждой точке, сделать вывод о существовании экстремума.
4. Найти экстремум функции.
Пример 2.Найти экстремум функции 
.
Решение.
1. Найдем частные производные: 
.
2. Найдем стационарные точки, решив систему уравнений:
— стационарная точка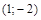 
.
3. Найдем частные производные 2-го порядка:
В точке 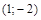экстремума нет.
Пример 3.Найти экстремум функции 
.
Решение.
1. 
2. Найдем стационарные точки:
– две стационарные точки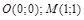 
.
3. Найдем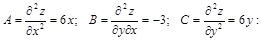 
а) найдем 
для точки О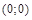 
,
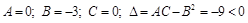значит, экстремума в точке 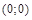не нет.
б) найдем для точки 
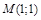
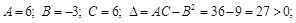
. Функция имеет минимум в точке 
.
4. 
.