Вычисление длины дуги кривой

Пусть кривая на плоскости имеет уравнение 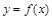. Необходимо найти длину дуги 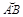этой кривой, ограниченной прямыми 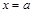и .

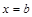Разобьем отрезок 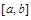на п частей точками

.

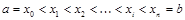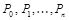— соответствующие точки на графике .

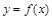Обозначим 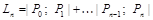— длину ломаной с вершинами в этих точках.

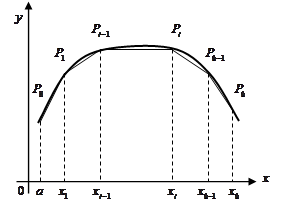Определение 1.Если существует предел 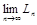, который не зависит от способа разбиения отрезка 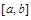, то этот предел называется длиной дуги графика 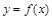на отрезке .

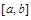Теорема 1. Если на отрезке 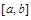функция 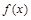и ее производная непрерывны, то длина дуги кривой 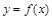, ограниченной прямым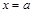и и 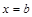, вычисляется по формуле

. (1)

Пример 1.Найти длину дуги кривой .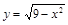

Решение. Область определения кривой . Тогда

.

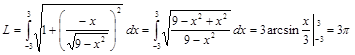Если дуга задана параметрически уравнениями 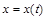, , 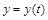, то ее длина находится по формуле

(2)

Пример 2.Вычислить длину дуги кривой, заданной параметрически

.

Решение. Найдем 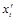и :

, .

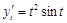Вычисляем дифференциал длины дуги

.

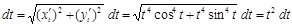Итак, длина дуги

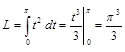ед. длины.

Если кривая задана уравнениям в полярных координатах 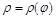, где 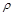– полярный радиус, а – полярный угол, то длина дуги находится по формуле

, (3)

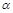где и 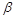– значение на предельных точках дуги.

Пример 3.Вычислить длину дуги кривой, заданной уравне-нием в полярных координатах

.

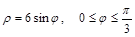Решение. Найдем :

.

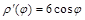Вычисляем дифференциал длины дуги:

,

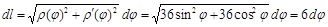тогда, длина дуги

.

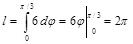Вычисление объемов тел вращения

Определение 1. Телом вращения называют пространствен-ную фигуру, которую можно получить вращением некоторой криволинейной трапеции вокруг оси .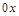

Рассмотрим в плоскости кривую 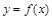, ограниченную абсциссами и .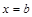

Разобьем тело вращения на п полос шириной .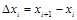

Тогда полоса от вращения части тела шириной даст объем:

.

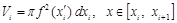Объем тела вращения приближенно определяется суммой

.

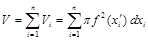Последняя сумма есть интегральная и потому

. (1)

Определение 2. Поверхностью вращенияназывают пространственную фигуру, которая образовывается вращением вокруг заданной прямой некоторой направленной простой дуги.

Площадь поверхности вращения можно найти по формуле

. (2)

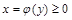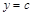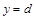
Если криволинейная трапеция ограничена графиком непрерывной функции , прямыми , , , то объем тела вращения, образованного вращением этой трапеции вокруг оси 0у равняется

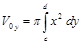. (3)

Пример 1. Вычислить объем тела вращения, ограниченного линиями , , 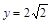вокруг оси 0у.

Решение.

.

Формула объема тела вращения обобщается на случай тела, образованного вращением вокруг оси 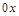криволинейной трапеции , образованной графиками функци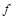й и , каждая из которых определена и непрерывна на отрезке 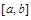, причем эти функции такие, что 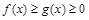для всех . Объем такого тела вычисляется по формуле

. (4)

Пример 2.Найти объем 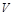тела, которое образовывается вращением вокруг оси 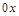фигуры, ограниченной линиям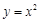и и .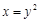

Решение. Точками пересечения лини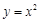й и 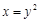(обе линии – параболы) есть точки с абсциссами 0 и 1. Поэтому, воспользовавшись формулой (11), будем иметь

.

Пример 3.Вычислить объем тела, образованного прямыми и при их вращении вокруг оси абсцисс.

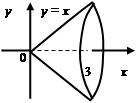Решение.

Имеем

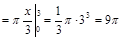куб. ед.

Если кривая линия задается в параметрической форме уравнениями

, причем ,

то объем тела вращения вычисляется по формуле:

, (5)

а площадь поверхности тела вращения:

. (6)

Пример 4. Вычислить объем и поверхность тела вращения, образованного одной аркой циклоиды

вокруг оси .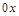

Решение.

.

.
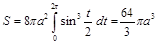