Задание 1.2. Для данной матрицы М

a) получить обратную матрицу М^-1;

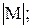б) вычислить определитель

в) получить транспонированную матрицу М^Т;

г) выделить элемент М_i,j;

д) выделить столбец Мⁱ.

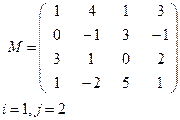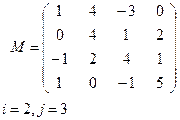Вариант 1 Вариант 2

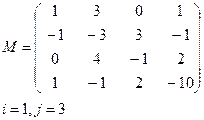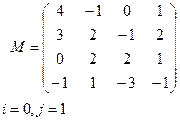Вариант 3 Вариант 4

Вариант 5 Вариант 6

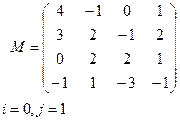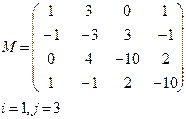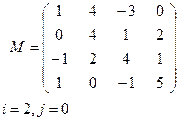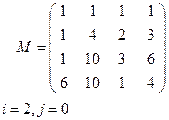Вариант 7 Вариант 8

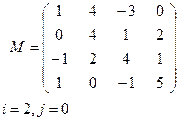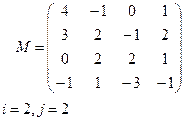Вариант 9 Вариант 10

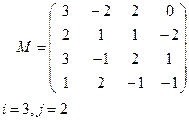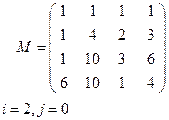Вариант 11 Вариант 12

Задание 1.3 Построить график функции и поменять вид кривой на зеленый пунктир.

1.		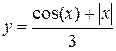7.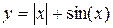
2.		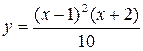8.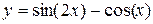
3.		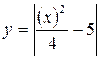9.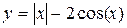
4.		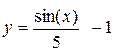10.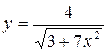
5.		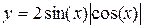11.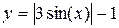
6.		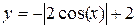12.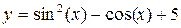

Порядок выполнения задания:

1. Введите функцию.

2. В панели математических знаков выбрать кнопку с изображением графика.

3. В палитре графиков щелкнуть на кнопке с изображением двумерного графика.

4. Ввести в место ввода шаблона по оси Х имя независимой переменной – х, а в место ввода шаблона по оси У имя зависимой переменной – у(х).

5.Нажать правую клавишу мыши на графике, выбрать меню Формат графика, во второй вкладке, появившегося окна изменить вид и цвет графика.

Задание 1.4 Построить график функции с условием на заданном интервале.

Порядок выполнения задания:

1. Для задания функции с условием используйте функцию if:

If(условие, выражение1, если условие выполнено, выражение2 если условие не выполнено).

2. Для изменения интервала измените числа, стоящие в углах рамки графика по оси Х.

1.

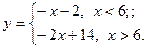
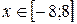
2.

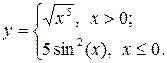
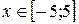
3.

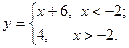
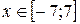
4.

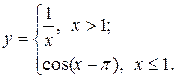
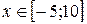
5.

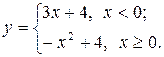
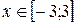
6.

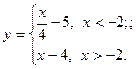
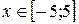
7.

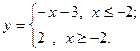
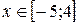
8.

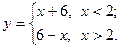
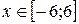
9.

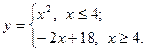
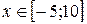
10.

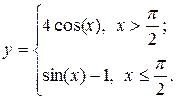
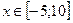
11.

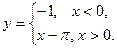
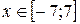
12.

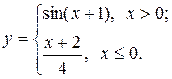
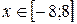
Практическая работа №2. Решение систем линейных уравнений в системе MathCad

Линейные системы имеют в вычислениях очень большое значение, так как к ним может быть приведено приближенное решение широкого круга задач. Так, основными источниками возникновения СЛАУ являются теория электрических цепей, уравнения балансов и сохранения в механике, гидравлике и т.п.

Пусть дана система n линейных алгебраических уравнений с n неизвестными:

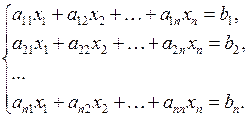(1)

Или в матричной форме:

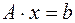;(2)

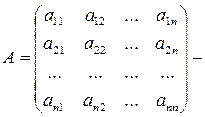где (3)

- матрица коэффициентов системы (1);

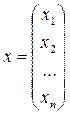- вектор неизвестных; 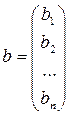- вектор свободных членов.

Если матрица A неособенная, т.е.

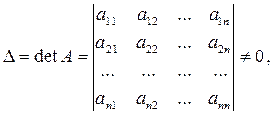(4)

то система (1) или эквивалентное ей матричное уравнение (2) имеют единственное решение.

Методы решения моделей в форме СЛАУ делятся на две группы: прямые итерационные.

Прямые методы позволяют получить решение системы (1) за конечное число шагов. Итерационные методы построены по принципу многократного вычисления последовательных приближений, сходящихся к искомому решению. Чем больше требуемая точность вычисления решения, тем большее количество итераций потребуется произвести. К прямым методам относятся метод обратной матрицы, метод Гаусса и его модификации, , метод Крамера, и др. К разряду итерационных методов принадлежат метод простой итерации, Зейделя и пр.

Метод Крамера

Одним из способов решения системы линейных уравнений является правило Крамера, согласно которому каждое неизвестное представляется в виде отношения определителей:

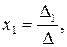
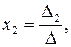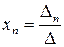…, , (5)

где D - определитель системы (1),

D_i – определители, полученные путем замены i-го столбца столбцом свободных членов системы (1).