Система с алгоритмом адаптации
На основе второго метода Ляпунова
Цель работы: изучение свойств непрерывной адаптивной системы, синтезированной на основе второго метода Ляпунова; исследование влияния параметров возмущений на качество работы системы.
Основные сведения
Второй метод Ляпунова нашел применение в задачах синтеза адаптивных регуляторов. Рассмотрим процедуру синтеза для линейного объекта управления (ОУ), модель которого имеет вид
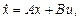
где хÎRn – вектор состояния, nÎRm – вектор управления; A, B – постоянные матрицы параметров объекта управления, dim A = nxn, dim B =
= nxm. Коэффициенты матриц А, В заранее не известны. Известно лишь, что значения коэффициентов ограничены сверху и снизу, т.е.
 для всех i, j.
для всех i, j.
Вектор состояния считается доступным измерению, поэтому y = x,
y – вектор выходных переменных.
Желаемая динамика задается эталонной моделью вида
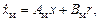
где хмÎRn – вектор состояния эталонной модели; rÎRm – вектор задающих воздействий. Выбор эталонной модели зависит от требований, предъявляемых к замкнутой системе (времени переходного процесса, перерегулирования, астатизма и т.д.). Эталонная модель должна быть устойчивой, т.е. матрица коэффициентов Ам – гурвицева, поэтому уравнение det(pI – Aм) = 0 имеет все корни с отрицательной вещественной частью, I – единичная матрица соответствующей размерности, Вм – матрица полного ранга.
Пусть цель функционирования системы задана предельным уравнением
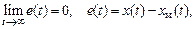
где e(t) – ошибка системы.
Объект управления подвержен влиянию параметрических возмущений. Поэтому в дальнейшем рассмотрим синтез системы с параметрической адаптацией.
Сначала полагаем, что параметры ОУ известны. Для получения структуры «идеального» регулятора запишем уравнение в отклонениях
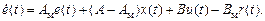
Условие разрешимости задачи синтеза имеет вид
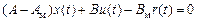 ,
,
разрешая это уравнение относительно u (t), имеем
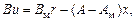
домножим слева каждую часть уравнения на BT
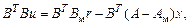
полагаем det(BTB) ¹ 0, тогда
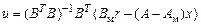 .
.
Если реализовать найденный закон управления, то система будет описываться уравнением
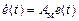 .
.
Решение этого уравнения равномерно асимптотически устойчиво в силу гурвицевости матрицы Ам. Следовательно, при «идеальном» законе управления поставленная цель достигается.
Уравнение «идеального» закона управления можно записать в виде
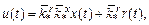
где 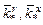 – матрицы «идеальных» коэффициентов регулятора. Соотношения между коэффициентами при х:
– матрицы «идеальных» коэффициентов регулятора. Соотношения между коэффициентами при х:
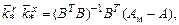
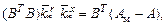
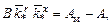
для коэффициентов при r:
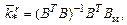
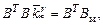
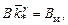
кроме того
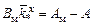 .
.
Полученные условия называются условиями согласования модели и ОУ.
«Идеальный» закон управления не реализуем, так как параметры ОУ не известны. Поэтому выполним замену идеальных коэффициентов регулятора ( 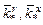 ) настраиваемыми (kr, kx). Структура регулятора описывается уравнением
) настраиваемыми (kr, kx). Структура регулятора описывается уравнением
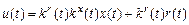 . (3.1)
. (3.1)
На следующем этапе расчета системы определяются уравнения, в соответствии с которыми настраиваются коэффициенты регулятора, т.е. алгоритмы изменения kr, kx. Получим описание обобщенного настраиваемого объекта в отклонениях. Введем обозначения
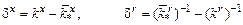 ,
,
тогда
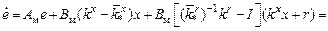
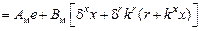 .
.
Введем расширенную матрицу отклонений настраиваемых коэффициентов от их «идеальных» значений
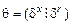
и вектор сенсоров, элементы которого измеряются или вычисляются на основе измерений
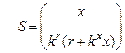 , dim S = p x 1, p = n + m.
, dim S = p x 1, p = n + m.
Уравнение для ошибки примет вид
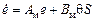 .
.
Для исследования системы используем функцию вида
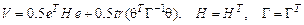 ,
,
где tr (.) – след матрицы (сумма элементов главной диагонали).
Определим производную функции V по времени:
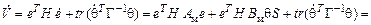
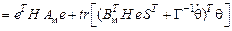 .
.
Вторая составляющая уравнения обращается в ноль, если
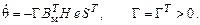
Производная исследуемой функции принимает вид
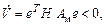
отрицательная определенность функции следует из гурвицевости матрицы коэффициентов эталонной модели. Матрица Н удовлетворяет уравнению Ляпунова:
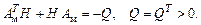
Полагая медленное изменение коэффициентов 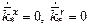 и учи-тывая ранее введенные обозначения, получим вид алгоритмов адаптации:
и учи-тывая ранее введенные обозначения, получим вид алгоритмов адаптации:
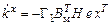 , (3.2)
, (3.2)
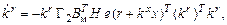 (3.3)
(3.3)
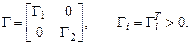
Методические указания
Рассматривается линейный одноканальный объект управления (1.18), (1.19) с параметрическими возмущениями. Желаемая динамика системы задается уравнением эталонной модели (1.20) по требованиям к качеству переходных процессов, приведенных в табл. 1.1 (статическая ошибка работы системы равна 5 %). В системе эталонная модель реализуется в виде линейного динамического звена второго порядка, дифференциальное уравнение, записанное относительно выходной переменной, имеет вид
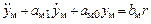 .
.
В данном случае основной контур (3.1) описывается уравнением
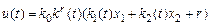 , (3.4)
, (3.4)
где k0 = const. Алгоритм адаптации (3.2), (3.3) преобразуется к виду
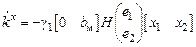 ,
,
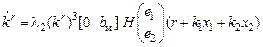 , (3.5)
, (3.5)
где γ1, γ2= const – коэффициенты передачи адаптора, e1= x1 – xм1,
e2 = x2 – xм2, xм1 = yм, xм2 = 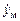 , kx =
, kx = 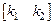 , dimH = 2 x 2, H = const,
, dimH = 2 x 2, H = const,
H = HT, H > 0, H – матрица коэффициентов квадратичной формы, выбранной для исследования устойчивости адаптивной системы, V = xT H x. Элементы матрицы H определяются как решение матричного уравнения Ляпунова
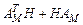 = – Q, Q = QT, Q > 0. (3.6)
= – Q, Q = QT, Q > 0. (3.6)
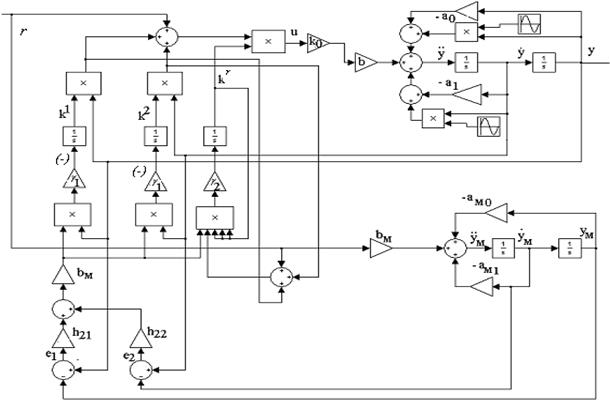
Схема системы с нестационарным объектом управления и измеряемой производной выходной переменной изображена на рис. 3.1.
Порядок работы
3.1. Определить элементы матриц 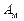 ,
, 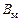 ,
, 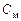 по заданным требованиям к качеству процессов (см. табл. 1.1).
по заданным требованиям к качеству процессов (см. табл. 1.1).
3.2. Вычислить элементы матриц H как решение уравнения Ляпунова (3.6), полагая 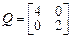 .
.
3.3. Записать уравнения алгоритмов адаптации (3.5) с вычисленными значениями коэффициентов.
3.4. Собрать схему эталонной модели (1.20) на интегрирую-
щих элементах. Получить переходную характеристику 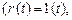
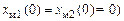 . Определить показатели качества: σ %, tn.
. Определить показатели качества: σ %, tn.
3.5 Собрать схему адаптивной системы (рис. 3.1), объект управления моделировать по схеме, приведенной на рис. 1.1 (см. лаб. работу
№ 1). Получить графики переходной характеристики системы (y(t)), управляющего воздействия(u (t))и процессов на выходе адаптора ( 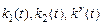 ) при r (t) = 1(t), нулевых начальных условиях по координатам состояния, g1=10,g2 =1, kr (0) = 1. Определить показатели качества (s %, tn, tna).
) при r (t) = 1(t), нулевых начальных условиях по координатам состояния, g1=10,g2 =1, kr (0) = 1. Определить показатели качества (s %, tn, tna).
3.6. Изменить значения коэффициентов передачи адаптора так, чтобы показатели качества выходного процесса соответствовали эталонным значениям, полученным в п. 3.4. Сравнить переходные характеристики и процессы в адапторе с результатами п. 3.5 по s %, tn, tna.
3.7. Изменить начальные условия в объекте (x1(0) = –1), x2(0) = 1), получить вид y (t), u (t), 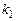 (t), k2(t),
(t), k2(t), 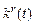 . Моделирование провести при g2= 1 и различных g1: g1 = 1,g1 = 10. Сравнить результат с п. 3.5.
. Моделирование провести при g2= 1 и различных g1: g1 = 1,g1 = 10. Сравнить результат с п. 3.5.
3.8. Изменить последовательно параметры объекта а0, а1, b в 2 раза, выполнить задание п. 3.5.
3.9. Изменить модель объекта управления 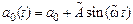 ,
, 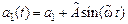 . Провести моделирование при нулевых начальных условиях и различных значениях
. Провести моделирование при нулевых начальных условиях и различных значениях 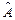 ,
, 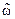 : а)
: а) 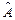 =1,
=1, 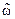 =1, б)
=1, б) 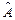 = 1,
= 1, 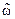 = 10, в)
= 10, в) 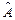 = 10,
= 10, 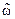 = 1. Для достижения эталонных показателей качества изменить значения
= 1. Для достижения эталонных показателей качества изменить значения 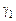 ,
, 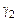 .
.
3.10*. Построить зависимость umaxот a (см. п. 3.8 лаб. работы № 1).
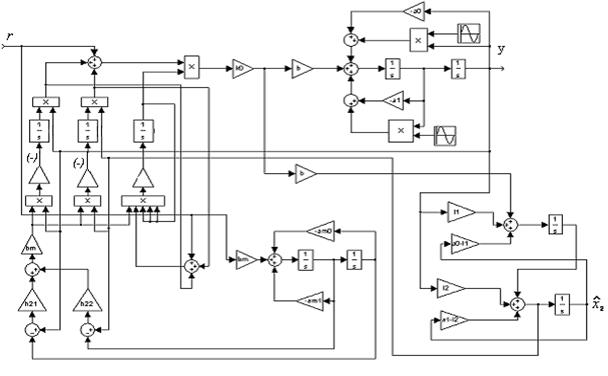
3.11 Выполнить расчет наблюдателя состояния (см. методические указания к лаб. работе № 1). Собрать схему системы с наблюдателем (рис. 3.2). Выполнить исследование системы, повторив пп. 3.5, 3.6, 3.9.
| |
| |
Содержание отчета
1. Цель работы.
2. Исходные данные.
4. Структурная схема адаптивной системы.
5. Расчет параметров адаптивного регулятора и наблюдателя; уравнения адаптивной системы с вычисленными значениями параметров.
6. Графики процессов пп. 3.4–3.11, график зависимости umaxот a.
7. Выводы по работе.
5. Контрольные вопросы
1. Гипотеза квазистационарности.
2. Постановка задачи адаптивного управления.
3. Основные этапы синтеза беспоисковых адаптивных систем.
4. Последовательность расчета адаптивной системы на основе второго метода Ляпунова.
5. Влияние начальных условий в адапторе на свойства системы.
6. Влияние темпа параметрических возмущений на свойства системы.
7. Определение закона управления.
8. Определение алгоритма адаптации.
9. Структурная схема адаптивной системы.
Лабораторная работа № 6
