Оценка погрешности определения момента инерции
1. Найти и сравнить систематическую и случайную ошибки определения t. Случайную ошибку Δt вычислить по формуле
DtСЛ = a 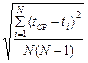 .
.
Для доверительной вероятности P = 0,95 и числа измерений N = 5 коэффициент Стьюдента a = 2,8.
Систематическая ошибка DtСИСТ определяется ошибкой, связанной с конечной скоростью реакции человека, которую можно принять равной 0,1 с: t = tСР + DtСИСТ.
Полную ошибку рассчитать по формуле
Dt = 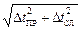 ,
,
где DtПР – приборная ошибка секундомера.
2. Рассчитать и занести в таблицу 4 относительные ошибки определения величин t, m и d.
Таблица 4
| Положение оси вращения | 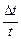 | 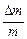 | 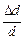 | J ± DJ, кг×м2 (метод колебаний) | J кг×м2 (метод приведенной длины) |
| Призма 1 | |||||
| Призма 2 |
3. Рассчитать максимальную абсолютную ошибку определения первым методом момента инерции по формуле
DJ = J 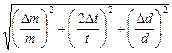 .
.
Результаты определения момента инерции с указанием абсолютной ошибки занести в таблицу 4.
Примечание. Значения величин g и p известны с большей точностью, и следовательно относительные ошибки, вносимые округлением этих величин, могут быть сделаны как угодно малыми, то есть заведомо меньшими, чем ошибки измерения остальных величин (m, d, T). Практически это означает, что при вычислениях значения g и p достаточно принять равными 9,81 м/с2 и 3,14 соответственно.
Контрольные вопросы
1. Дайте определение гармонических колебаний.
2. Что называется математическим маятником, физическим маятником?
3. Что называется приведенной длиной физического маятника?
4. Как выводиться формула периода колебаний физического маятника?
Список литературы
1. Детлаф А.А., Яворский Б.М. Курс физики. –М.: Высш. шк. – 2000.
2. Савельев И.В. Курс физики. – Т. 2. – М.: Наука – 1998 и далее.
3. Трофимова Т.И. Курс физики. – М., 2000 и далее.
4. Селезнёв В.А., Тимофеев Ю. П. Вводное занятие в лабораториях кафедры физики. – М.: МИИТ. – 2011. – 38 с.
Работа 5а
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
Цель работы.Определение ускорения свободного падения методом, основанным на свойстве взаимной обратимости центра качания и точки подвеса физического маятника.
Приборы и принадлежности: физический маятник, секундомер.
Введение
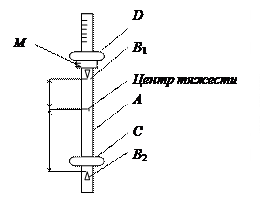
Период колебаний физического маятника (см. рис. 3) определяется по формуле
T = 2p 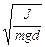 , (1)
, (1)
где J – момент инерции относительно оси подвеса;
m – масса маятника;
d – расстояние между осью вращения и центром тяжести маятника.
 |
 d1
d1
d2
Рис. 3
Длина математического маятника с периодом колебаний, равным периоду колебаний данного физического маятника, называется приведенной длиной физического маятника. Эта величина определяется соотношением
lП = 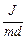 . (2)
. (2)
Вывод формул (1) и (2) приведен во введении к работе 5.
Точка, находящаяся на расстоянии lП от оси вращения по линии, проходящей через центр тяжести, называется центром качания физического маятника. Можно показать, что если ось вращения поместить в центр качания, то маятник будет совершать колебания с тем же периодом. Для этого подставим в формулу (2) момент инерции в соответствии с теоремой Гюйгенса-Штейнера:
J = J0 + md2.
Получим:
lП = 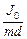 + d, (3)
+ d, (3)
где J0– момент инерции тела относительно оси, проходящей через центр тяжести тела параллельно оси, проходящей через точку подвеса.
Заметим, что из выражения (3) следует
d = 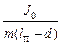 . (4)
. (4)
Если подвесить маятник так, чтобы ось вращения проходила через центр качания, то она будет находиться от центра тяжести на расстоянии lП – d. Приведенную длину этого перевернутого маятника можно найти по формуле (3), учитывая, что теперь расстояние от оси вращения до центра тяжести lП– d, а m и J0 остались прежними. Центр качания перевернутого маятника по формуле (3) будет находиться от оси вращения на расстоянии
lП¢ = 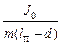 + (lП – d).
+ (lП – d).
Учитывая выражение (4), находим, что
lП = lП¢.
Таким образом, во всяком физическом маятнике на прямой, проходящей через центр тяжести (центр инерции), можно указать пары точек, лежащих по разные стороны от центра тяжести и являющихся взаимно обратимыми, то есть через них проходят оси вращения, относительно которых период колебаний маятника одинаков.
