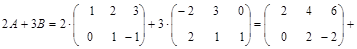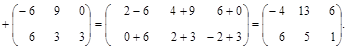Матрицы и действия над ними

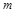Определение 1. МатрицейАразмера называется прямоугольная таблица из строк и 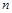столбцов, которая состоит из чисел или других математических выражений 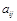(которые называются элементами матрицы), , .

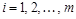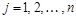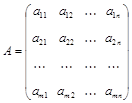
Если количество строк 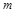одинаково с количеством столбцов 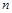, то такая матрица называется квадратной порядка п, при 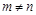матрица называется прямоугольной.

Элементы 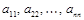квадратной матрицы образуют главную диагональ матрицы, а элементы 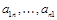– вспомогательную диагональ.

Квадратная матрица, у которой все элементы на главной диагонали равны единице, а другие - нулю, называется единичной.

Определение 2. Рангом матрицы называют наибольший порядок ее миноров, отличных от нуля.

Ранг матрицы обозначают 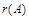или 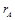или просто 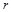. Ранг матрицы можно находить методом элементарных преобразований.

Элементарными преобразованиями матрицы называют такие действия:

1) перестановка строк (столбцов) матрицы;

2) умножение всех элементов строки (столбца) на число ;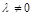

3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на некоторое число.

Все эти преобразования не изменяют ранг матрицы, но с их помощью матрицу сводят к матрице, у которой ниже главной диагонали все элементы – нули. Тогда ранг матрицы равняется количеству элементов главной диагонали, отличных от нуля.

Пример 1. Найти ранг матриц:

а) 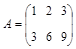, б) .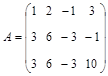

Решение. Ранг матриц будем находить методом элементарных преобразований.

а) Элементы первой строки матрицы умножим на (–3) и прибавим к соответствующим элементам второй строки матрицы А:

.

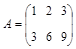
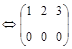Отсюда вытекает, что ранг этой матрицы равняется 1 (ниже главной диагонали – нуль и один элемент главной диагонали ).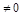

б) Преобразуем матрицу аналогично предыдущей:

.

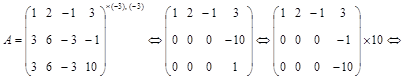
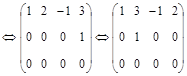Отсюда вытекает, что .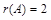

Определение 3.Матрица 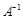называется обратной матрицей к матрице А, если выполняются равенства

,

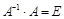где Е – единичная матрица.

Не каждая матрица имеет обратную. В алгебре матриц доказано, что матрица А имеет обратную матрицу 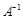при выполнении двух условий:

1) матрица А квадратная;

2) определитель |А| матрицы А не равен нулю.

Обратную матрицу 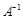к матрице А можно найти по формуле

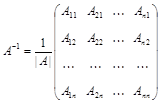
где 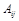– алгебраические дополнения элементов 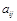– матрицы А.

Пример 2. Найти обратную матрицу к матрице .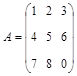

Решение.а) найдем :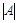

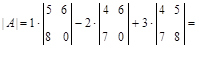
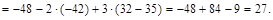
Так как 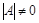, матрица 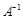существует.

б) найдем алгебраические дополнения всех элементов матрицы А:

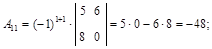
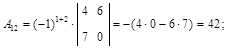
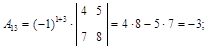
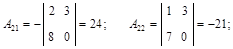
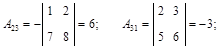
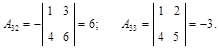
в) обратная матрица имеет вид:

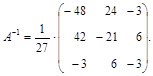
Определение 4. Суммой матриц 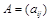и 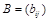одинако-вого размера называется матрица 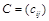, где .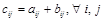

Для любых матриц А, В и С одного размера выполняются равенства:

1. А + В = В + А (коммутативность);

2. (А + В) + С = А + (В + С) = А + В + С (ассоциативность)

Определение 5. Произведением матрицы 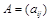на число 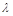называется матрица 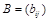того же размера, что и матрица А, где .

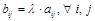Свойства операции умножения матрицы на число:

1) 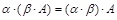(ассоциативность);

2) 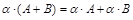(дистрибутивность относительно сложения матриц);

3) 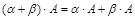(дистрибутивность относительно сложения чисел).

Свойства операции умножения матриц:

1) 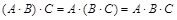(ассоциативность);

2) 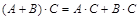(дистрибутивность);

3) 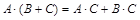(дистрибутивность);

4) 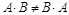(отсутствие коммутативности).

Определение 6. Произведением матриц А и В называется матрица С, элементы которой 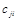являются скалярным произведением векторов-строк 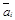матрицы А на вектор-столбец 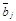матрицы В:

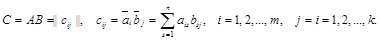
Пусть даны две матрицы: А – размера 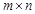и В – размера 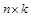. Будем рассматривать матрицу А как совокупность векторов-строк 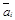размерности п каждый, а матрицу В – как совокупность k векторов-столбцов 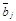, которые содержат по п координат каждый:

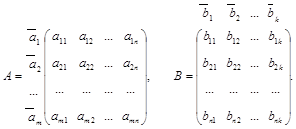
Длина сроки матрицы А равняется высоте столбца матрицы В, и потому скалярное произведение этих векторов имеет смысл.

Пример 3. Найти произведение матриц:

.

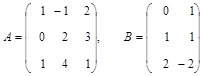Решение. Поскольку число столбцов матрицы А равняется числу строк матрицы В, то произведение матриц АВ имеет смысл. Получаем в произведении матрицу размера :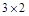

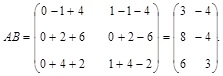
Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.

Определение 7. Транспонированной к матрице 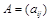называется матрица 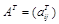такая, что 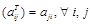(т.е. все строки которой равняются соответствующим столбцам матрицы А).

Матрица В, полученная из матрицы А с помощью элементарных преобразований, называется эквивалентной к матрице А (обозначается ).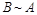

Пример 4. Найти 2А + 3В, где:

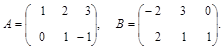
Решение.