После изучения тем РАЗДЕЛА 3
Студент должен выполнить контрольную работу № 3
ЗАДАНИЯ КОНТРОЛЬНЫХ РАБОТ
КОНТРОЛЬНАЯ РАБОТА № 1 
Введение в математический анализ. Дифференциальное исчисление функции одной переменной.
ЗАДАНИЕ 1
Найти пределы функций.
1.1  a)
a) 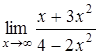 , б)
, б) 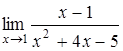 , в)
, в) 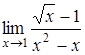 ,
,
г) 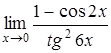 , д)
, д) 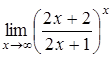 .
.
1.2 а) 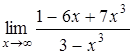 , б)
, б) 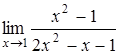 , в)
, в) 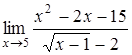 ,
,
г) 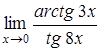 , д)
, д) 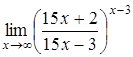 .
.
1.3 а) 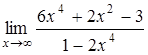 , б)
, б) 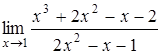 , в)
, в) 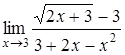 ,
,
г) 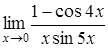 , д)
, д) 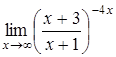 .
.
1.4 а) 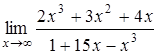 , б)
, б) 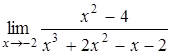 , в)
, в) 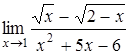 ,
,
г) 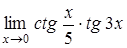 , д)
, д) 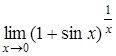 .
.
1.5 а) 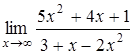 , б)
, б) 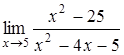 , в)
, в) 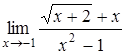 ,
,
г) 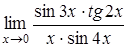 , д)
, д) 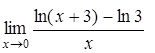 .
.
1.6 а) 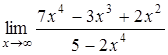 , б)
, б) 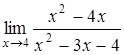 , в)
, в) 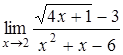 ,
,
г) 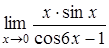 , д)
, д) 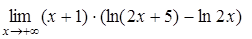 .
.
1.7 а) 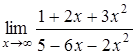 , б)
, б) 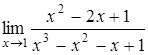 , в)
, в) 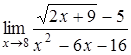 ,
,
г) 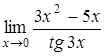 , д)
, д) 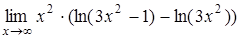 .
.
1.8 а) 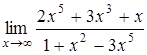 , б)
, б) 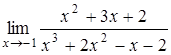 , в)
, в) 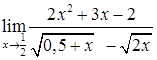 ,
,
г) 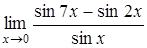 , д)
, д) 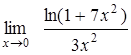 .
.
1.9 а) 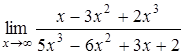 , б)
, б) 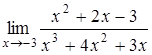 , в)
, в) 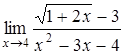 ,
,
г) 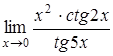 , д)
, д) 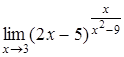 .
.
1.10 а) 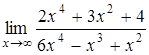 , б)
, б) 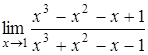 , в)
, в) 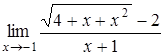 ,
,
г) 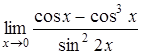 , д)
, д) 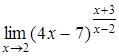 .
.
ЗАДАНИЕ 2
Найти производные 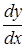 данных функций.
данных функций.
2.1 а) 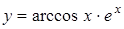 ; б)
; б) 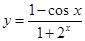 ; в)
; в) 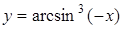 ;
;
г) 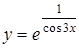 ; д)
; д) 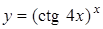 .
.
2.2 а) 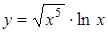 ; б)
; б) 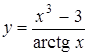 ; в)
; в) 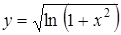 ;
;
г) 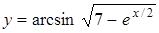 ; д)
; д) 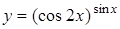 .
.
2.3 а) 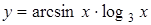 ; б)
; б) 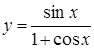 ; в)
; в) 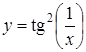 ;
;
г) 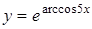 ; д)
; д) 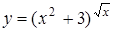 .
.
2.4 а) 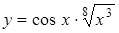 ; б)
; б) 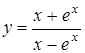 ; в)
; в) 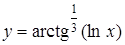 ;
;
г) 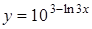 ; д)
; д) 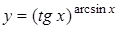 .
.
2.5 а) 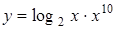 ; б)
; б) 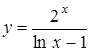 ; в)
; в) 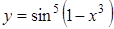 ;
;
г) 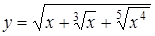 ; д)
; д) 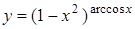 .
.
2.6 а) 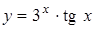 ; б)
; б) 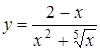 ; в)
; в) 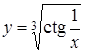 ;
;
г) 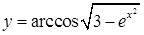 ; д)
; д) 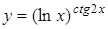 .
.
2.7 а) 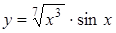 ; б)
; б) 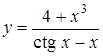 ; в)
; в) 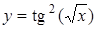 ;
;
г) 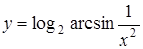 ; д)
; д) 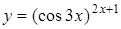 .
.
2.8 а) 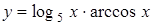 ; б)
; б) 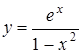 ; в)
; в) 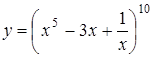 ;
;
г) 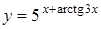 ; д)
; д) 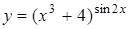 .
.
2.9 а) 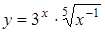 ; б)
; б) 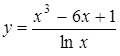 ; в)
; в) 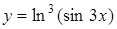 ;
;
г) 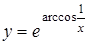 ; д)
; д) 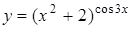 .
.
2.10 а) 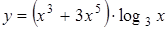 ; б)
; б) 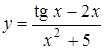 ; в)
; в) 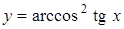 ;
;
г) 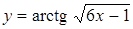 ; д)
; д) 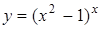 .
.
ЗАДАНИЕ 3
Провести полное исследование функций и построить их графики.
3.1. а) 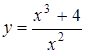 ; б)
; б) 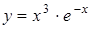 .
.
3.2. а) 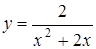 ; б)
; б) 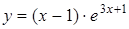 .
.
3.3. а) 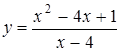 ; б)
; б) 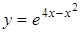 .
.
3.4. а) 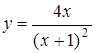 ; б)
; б) 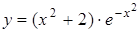 .
.
3.5. а) 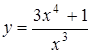 ; б)
; б) 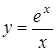 .
.
3.6. а) 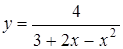 ; б)
; б) 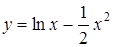 .
.
3.7. а) 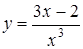 ; б)
; б) 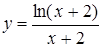 .
.
3.8. а) 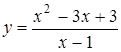 ; б)
; б) 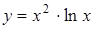 .
.
3.9. а) 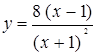 ; б)
; б) 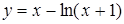 .
.
3.10. а) 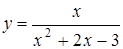 ; б)
; б) 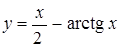 .
.
КОНТРОЛЬНАЯ РАБОТА № 2
Неопределённый и определённый интегралы
ЗАДАНИЕ 4
Вычислить неопределённые интегралы. В пунктах а) и б) результаты проверить дифференцированием.
4.1 а) 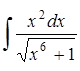 ; б)
; б) 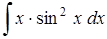 ;
;
в) 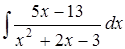 ; г)
; г) 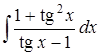 .
.
4.2 а) 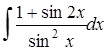 ; б)
; б) 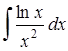 ;
;
в) 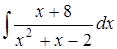 ; г)
; г) 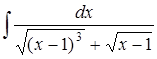 .
.
4.3 а) 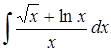 ; б)
; б) 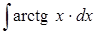 ;
;
в) 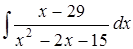 ; г)
; г) 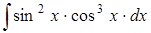 .
.
4.4 а) 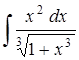 ; б)
; б) 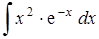 ;
;
в) 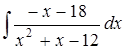 ; г)
; г) 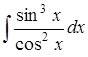 .
.
4.5 а) 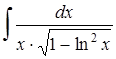 ; б)
; б) 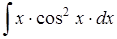 ;
;
в) 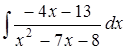 ; г)
; г) 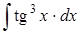 .
.
4.6 а) 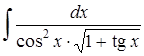 ; б)
; б) 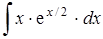 ;
;
в) 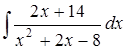 ; г)
; г) 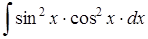 .
.
4.7 а) 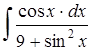 ; б)
; б) 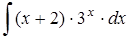 ;
;
в) 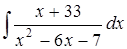 ; г)
; г) 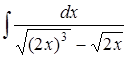 .
.
4.8 а) 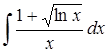 ; б)
; б) 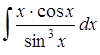 ;
;
в) 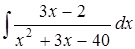 ; г)
; г) 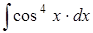 .
.
4.9 а) 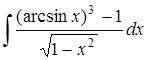 ; б)
; б) 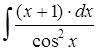 ;
;
в) 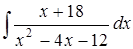 ; г)
; г) 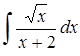 .
.
4.10 а) 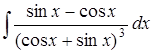 ; б)
; б) 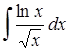 ;
;
в) 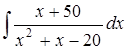 ; г)
; г) 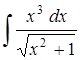 .
.
ЗАДАНИЕ 5.
Вычислить несобственный интеграл или доказать его расходимость.
5.1 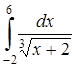 . 5.2
. 5.2 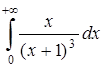 .
.
5.3 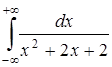 . 5.4
. 5.4 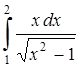 .
.
5.5 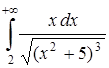 . 5.6
. 5.6 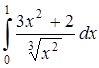 .
.
5.7 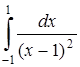 . 5.8
. 5.8 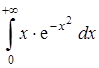 .
.
5.9 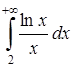 . 5.10
. 5.10 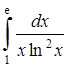 .
.
ЗАДАНИЕ 6
6.1. Вычислить площадь фигуры, ограниченной параболой 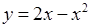 и прямой
и прямой 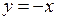 .
.
6.2. Вычислить площадь фигуры, ограниченной линиями
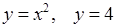 .
.
6.3. Вычислить площадь фигуры, ограниченной линиями
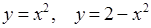 .
.
6.4. Вычислить площадь фигуры, ограниченной параболами
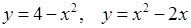 .
.
6.5. Вычислить объём тела, образованного вращением вокруг оси Ox фигуры, ограниченной параболой 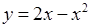 и прямой
и прямой 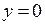 .
.
6.6. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 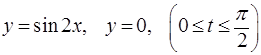 .
.
6.7. Вычислить длину дуги астроиды
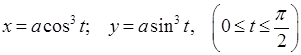 .
.
6.8. Вычислить длину дуги кривой 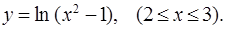
6.9. Вычислить длину дуги кривой
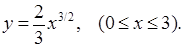
6.10. Вычислить длину дуги кривой
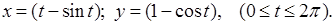
КОНТРОЛЬНАЯ РАБОТА № 3
Линейная алгебра, векторы, аналитическая геометрия.
ЗАДАНИЕ 7
Даны матрицы 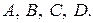
Найти матрицы 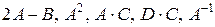 (с проверкой).
(с проверкой).
7.1
A= 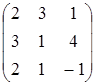 , B=
, B= 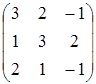 , C=
, C= 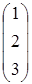 , D=
, D= 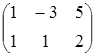 .
.
7.2
A= 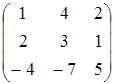 , B=
, B= 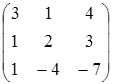 , C=
, C= 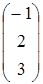 , D=
, D= 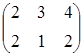 .
.
7.3
A= 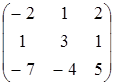 , B=
, B= 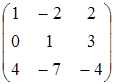 , C=
, C= 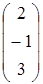 , D=
, D= 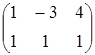 .
.
7.4
A= 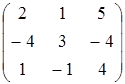 , B=
, B= 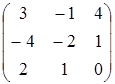 , C=
, C=  , D=
, D= 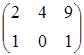 .
.
7.5
A= 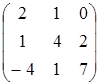 , B=
, B= 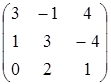 , C=
, C= 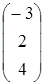 , D=
, D= 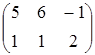 .
.
7.6
A= 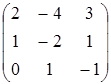 , B=
, B= 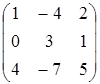 , C=
, C= 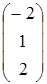 , D=
, D= 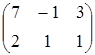 .
.
7.7
A= 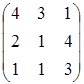 , B=
, B= 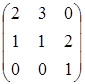 , C=
, C= 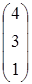 , D=
, D= 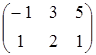 .
.
7.8
A= 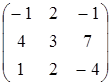 , B=
, B= 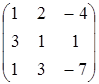 , C=
, C= 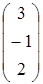 , D=
, D= 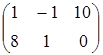 .
.
7.9
A= 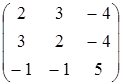 , B=
, B= 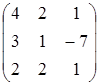 , C=
, C= 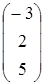 , D=
, D= 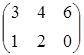 .
.

7.10
A= 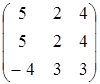 , B=
, B= 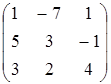 , C=
, C= 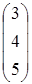 , D=
, D= 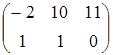 .
.
ЗАДАНИЕ 8
Даны координаты точек: 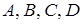 .
.
Найти: 1) длину вектора 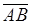 ,
,
2) угол между векторами 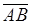 и
и 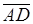 ,
,
3) уравнение прямой AB,
4) уравнение плоскости 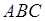 ,
,
5) угол между ребром 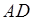 и гранью
и гранью 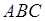 ,
,
6) объём пирамиды 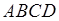 ,
,
7) уравнение высоты, опущенной из вершины 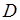 на грань
на грань 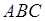 ,
,
8) сделать чертеж.
8.1 A (5, 1, 4 ); B (-7, 6, 5 ); C (3, -4, 3 ); D (0, 2, 9 ).
8.2 A (5, 2, 0 ); B (2, 5, 0 ); C (1, 2, 4 ); D (-1, 1, 1 ).
8.3 A (-2, 0, -4 ); B (-1, 7, 1 ); C (4, -8, -4 ); D (1, -4, 6 ).
8.4 A (2, -1, 2 ); B (1, 2, -1 ); C (3, 2, 1 ); D (-4, 2, 5 ).
8.5 A (-1, 2, -3 ); B (4, -1, 0 ); C (2, 1, -2 ); D (3, 4, 5 ).
8.6 A (1, -1, 1 ); B (-2, 0, 3 ); C (2, 1, -1 ); D (2, -2, -4 ).
8.7 A (1, 2, 0 ); B (1, -1, 2 ); C (0, 1, -1 ); D (-3, 0, 1 ).
8.8 A (1, 0, 2 ); B (1, 2, -1 ); C (2, -2, 1 ); D (2, 1, 0 ).
8.9 A (1, 3, 0 ); B (4, -1, 2 ); C (3, 0, 1 ); D (-4, 3, 5 ).
8.10 A (0, 3, 2 ); B (-1, 3, 6 ); C (-2, 4, 2 ); D (0, 5, 4 ).
ЗАДАНИЕ 9
Дана система линейных уравнений.
Решить её двумя способами: 1) методом Гаусса; 2) матричным методом.
9.1 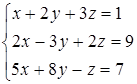 9.2
9.2 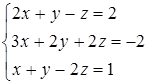
9.3 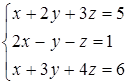 9.4
9.4 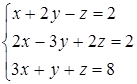
9.5 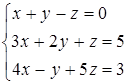 9.6
9.6 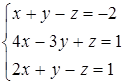
9.7 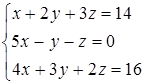 9.8
9.8 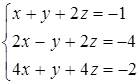
9.9 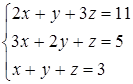 9.10
9.10 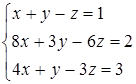
ОБРАЗЦЫ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ
