Разработка моделей приборов по описывающим их дифференциальным уравнениям в частных производных

5.3.1. Введение. Работа физического прибора основана на передаче информации между отдельными точками пространства, причем такие передачи связаны с временными задержками. Чтобы составить полную и адекватную модель прибора, необходимо ввести в нее в качестве параметров пространственные координаты и время. А это в конечном счете приводит к необходимости решения дифференциальных уравнений в частных производных, описывающих такие хорошо изученные приборы, как, например, диод или транзистор. Если рассматриваются приборы, принципы работы которых изучены недостаточно хорошо (примером может служить полевой транзистор), то при разработке их модели они разделяются на зоны, физические принципы поведения которых
Фиг. 5.1. Движение неосновных носителей в полупроводникерешения дифференциальных уравнений в частных производных, на основе которых получают схемные модели активных элементов.
достаточно ясны. Модель каждой зоны представляется упрощенной радиоэлектронной схемой; общая модель прибора образуется в результате соответствующего объединения моделей всех зон.
Такой эвристический подход оправдан, когда: а) не ясна физика работы прибора или нет четкого понимания используемого технологического процесса; б) приближенная модель обеспечивает получение достаточно точных результатов в конкретном схемном применении прибора.
Нужно, однако, учитывать, что к численному моделированию зачастую обращаются как раз тогда, когда оказывается, что схема работает иначе, чем предсказывают упрощенные модели активных элементов. В этих случаях как раз необходимо располагать более детальными и точными методами моделирования физических приборов с помощью дифференциальных уравнений в частных производных. В этом разделе будут изложены методы
5.3.2. Уравнение непрерывности. Большинство моделей полупроводниковых приборов в настоящее время основаны на предположении, что ток обусловлен движением неосновных носителей, т. е. перемещением носителей р-типа в полупроводнике n-типа, и наоборот.
Ток диффузии в полупроводнике n-типа описывается уравнением, связывающим число носителей р-типа, которые поступают в единицу объема, выходят из него и накапливаются в нем за единицу времени (фиг. 5.1). Это есть так называемое «уравнение непрерывности», в котором символически записано, что
 +
+

или
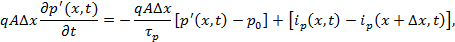
(5.1)
где q — заряд электрона; A — площадь поперечного сечения рассматриваемой единицы объема; 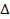 х — длина единицы объема; p'{x,t)—концентрация неосновных носителей; р0 — концентрация неосновных носителей при нулевом возбуждении (равновесная концентрация);
х — длина единицы объема; p'{x,t)—концентрация неосновных носителей; р0 — концентрация неосновных носителей при нулевом возбуждении (равновесная концентрация); 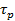 — время жизни носителей p-типа в полупроводнике n-типа. Поделив обе части (5.1) на
— время жизни носителей p-типа в полупроводнике n-типа. Поделив обе части (5.1) на 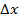 и перейдя к пределу при
и перейдя к пределу при 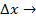 0, получим дифференциальное уравнение в частных производных
0, получим дифференциальное уравнение в частных производных
 (5.2)
(5.2)
Ток диффузии  x,t) связан с концентрацией неосновных носителей уравнением
x,t) связан с концентрацией неосновных носителей уравнением
ip=-qADp 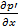 ,
,
где Dp — коэффициент диффузии. При этом уравнение (5.2) принимает вид
 .
.
Удобно ввести определение «избыточной» концентрации носителей
р(х, t) = р'(x, t) - p0.
Так как частные производные от p(x,t) и p'(x,t) одинаковы, то в окончательном виде уравнение диффузии записывается в следующей форме:
 (5.3)
(5.3)
Это уравнение является линейным дифференциальным уравнением в частных производных с постоянными коэффициентами. Далее будет показано, что схемная модель состоит из линейных элементов с фиксированными параметрами.
