Анализ устойчивости системы
Курсовая работа по дисциплине
«Основы теории управления»
Вариант VIII-2
Выполнил:
студент группы ИС-31
Корнеев К.Б.
Проверил:
Очина Л.Б.
Санкт-Петербург
2008 год.
Введение
В настоящее время системы автоматизированного управления применяются практически во всех отраслях производства. Это значительно упрощает труд рабочих, но для того чтобы полагаться на автоматы необходимо быть уверенным в их надёжности. Это свойство определяется устойчивостью системы. В ходе изучения курса основ теории управлениябыла предложена курсовая работа по анализу устойчивости системы
Вид структурной схемы:
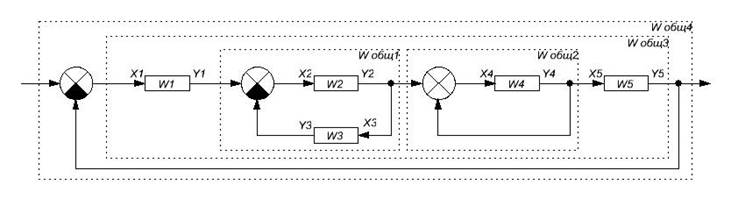
Математическое описание:
1) 
2) 
3) 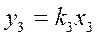
4) 
5) 
Значение коэффициентов:
| k1=4 k2=8 k3=2 k4=3 k5=6 | T2=0,1 с. T4=0,5с. |
1. По имеющимся дифференциальным уравнениям звеньев определим их передаточные функции Wi (P).
1). Пропорциональное звено(относится к классу позиционных динамических звеньев)
Y1(p)=k1X1(p) ; k1=4
W1(p)=k1=4
Временная переходная характеристика h(t):
x(t)=1(t)
h(t)=k*1(t)=k=4
Значение временной переходной характеристики определяется как значение коэффициента усиления, умноженное на единичное ступенчатое
График временной переходной характеристики:

Функция веса  (t):
(t):
x(t)= 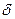 (t)
(t)
 (t)=k
(t)=k 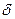 (t)=4
(t)=4 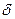 (t)
(t)
График функции веса:

Частотные характеристики:
а) Амплитудно-фазовая частотная характеристика (АФЧХ)
W(i  ) = W(p)|p=i
) = W(p)|p=i  =k
=k
P(  ) = k = 4
) = k = 4
Q(  ) = 0
) = 0
б) Амплитудная частотная характеристика (АЧХ)
 = 4
= 4
в) Фазовая частотная характеристика (ФЧХ)

2). Апериодическое звено 1го порядка (относится к классу позиционных динамических звеньев)
T2*Y2(p)*p+Y2(p)=k2*X2(p) ; k2=8 ; T2=0,1
Y2(p)*(T2p+1)=k2*X2(p)
W2(p)= 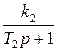
Временная переходная характеристика h(t):
y(t)=h(t)

График временной переходной характеристики:
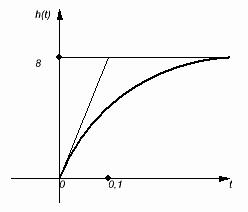
Функция веса  (t):
(t):
x(t)= 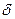 (t)
(t)
 (t)=?
(t)=?
 (t)=
(t)= 


График функции веса:

Частотные характеристики:
а) Амплитудно-фазовая частотная характеристика (АФЧХ)
W(i  ) = W(p)|p=i
) = W(p)|p=i  =
= 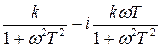
P(  ) = k = 4
) = k = 4
Q(  ) = 0
) = 0
б) Амплитудная частотная характеристика (АЧХ)
 0.99
0.99
в) Фазовая частотная характеристика (ФЧХ)

3). Пропорциональное звено(относится к классу позиционных динамических звеньев)
Y3(p)=k3X3(p) ; k3=2
W3(p)=k3=2
Временная переходная характеристика h(t):
x(t)=1(t)
h(t)=k*1(t)=k=4
График временной переходной характеристики:

Функция веса  (t):
(t):
x(t)= 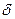 (t)
(t)
 (t)=k
(t)=k 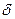 (t) =2
(t) =2 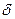 (t)
(t)
График функции веса:

Частотные характеристики:
а) Амплитудно-фазовая частотная характеристика (АФЧХ)
W(i  ) = W(p)|p=i
) = W(p)|p=i  =k
=k
P(  ) = k = 2
) = k = 2
Q(  ) = 0
) = 0
б) Амплитудная частотная характеристика (АЧХ)
 = 2
= 2
в) Фазовая частотная характеристика (ФЧХ)

4). Апериодическое звено 1го порядка (относится к классу позиционных динамических звеньев)
T4*Y4(p)*p+Y4(p)=k4*X4(p) ; k4=3 ; T4=0,5
Y4(p)*(T4p+1)=k4*X4(p)
W4(p)= 
Временная переходная характеристика h(t):
y(t)=h(t)

График временной переходной характериистики:

Функция веса  (t):
(t):
x(t)= 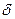 (t)
(t)
 (t)=?
(t)=?
 (t)=
(t)= 


График функции веса:

Частотные характеристики:
а) Амплитудно-фазовая частотная характеристика (АФЧХ)
W(i  ) = W(p)|p=i
) = W(p)|p=i  =
= 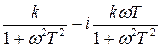
P(  ) = k = 3
) = k = 3
Q(  ) = 0
) = 0
б) Амплитудная частотная характеристика (АЧХ)

в) Фазовая частотная характеристика (ФЧХ)

5). Пропорциональное звено(относится к классу позиционных динамических звеньев)
Y5(p)=k5X5(p) ; k5=6
W5(p)=k5=6
Временная переходная характеристика h(t):
x(t)=1(t)
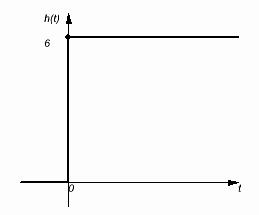
h(t)=k*1(t)=k=6
График временной переходной характеристики:
Функция веса  (t):
(t):
x(t)= 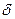 (t)
(t)
 (t)=k
(t)=k 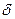 (t) =6
(t) =6 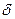 (t)
(t)
График функции веса:
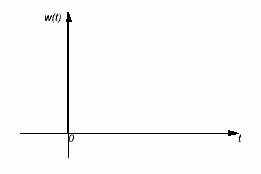
Частотные характеристики:
а) Амплитудно-фазовая частотная характеристика (АФЧХ)
W(i  ) = W(p)|p=i
) = W(p)|p=i  =k
=k
P(  ) = k = 6
) = k = 6
Q(  ) = 0
) = 0
б) Амплитудная частотная характеристика (АЧХ)
 = 6
= 6
в) Фазовая частотная характеристика (ФЧХ)

3. Определение выражения для общей передаточной функции системы в виде:
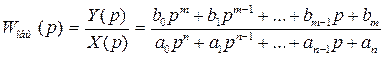 ,
,
где Y(p) – изображение выходной величины;
X(p) – изображение входной величины;
a0,a1,…,an; b1,b2,…,bm – постоянные коэффициенты.
Для этого определим выражения для частных передаточных функций, обозначенных на общей схеме системы как Wобщ.1, Wобщ.2, Wобщ.3,  Wобщ.4:
Wобщ.4:

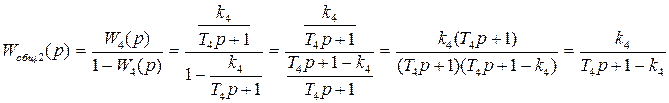
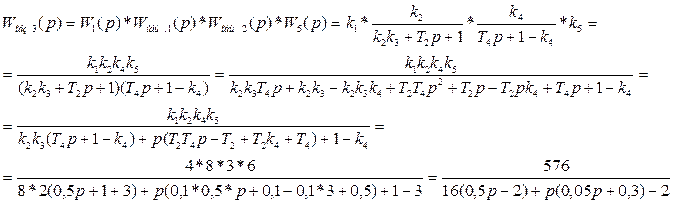
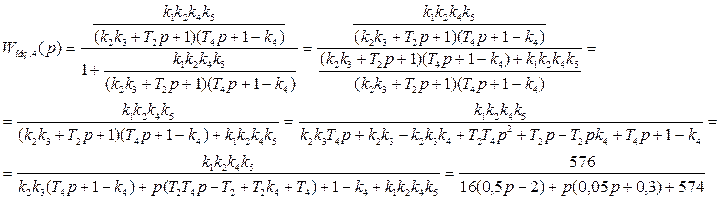
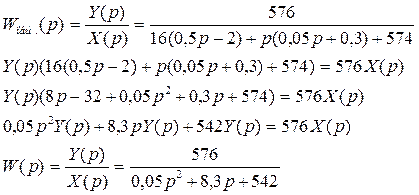
4. Составление дифференциального уравнения системы в виде:
 ,
,
где x(t) – входная величина;
y(t) – выходная величина;
a0, a1, … , an ; b0, b1, … , bm – постоянные коэффициенты.
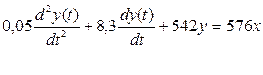
Анализ устойчивости системы
