Решения нелинейного уравнения
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ И ПРЕДПРИНИМАТЕЛЬСТВА
Пензенский филиал
Кафедра «Защита в чрезвычайных ситуациях»
Пояснительная записка
к курсовой работе
по дисциплине: «Информатика и программирование»
Тема: «Решение задач с помощью компьютера»
Выполнила:
Проверила: преподаватель
Реферат
Пояснительная записка 16 листов, 9 рисунков, 7 источников литературы и 3 приложения.
Программа, презентация, макрос, уравнение, система уравнений, матрица.
Цель курсовой работы: рассмотреть практическое применение компьютера для решения задач.
В процессе работы были изучены язык программирования Turbo Pascal, приложения Microsoft Excel и Microsoft PowerPoint.
В результате были разработаны программа по нахождению интеграла методом трапеции, рабочая книга Excel. 
Содержание
Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
Часть 1. Программа на языке Turbo Pascal. . . . . . . . . . . . . . . . . .5
Часть 2. Рабочая книга Excel. . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
2.1 Лист презентации. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
2.2 Лист меню. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..7
2.3 Решение нелинейного уравнения. . . . . . . . . . . . . . . . . . . . . . . 7
2.4 Решение системы линейных уравнений. . . . . . . . . . . . . . . . . . 7
2.5 Решение системы линейных уравнений в Matchad. . . . . . . . . . 8
2.6 Решение задачи оптимизации. . . . . . . . . . . . . . . . . . . . . . . . . .8
2.7 Решение экономической задачи. . . . . . . . . . . . . . . . . . . . . . . . 9
Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..10
Список используемой литературы. . . . . . . . . . . . . . . . . . . . . . . . 11
Приложение№ 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12
Приложение№ 2. . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . ..13
Приложение№ 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17
Введение
В последнее время в связи с бурным ростом средств вычислительной техники, внедрением компьютеров в нашу жизнь, всё большее количество ряда различных задач решается с помощью ЭВМ. Однако известно, что даже самый современный компьютер – это лишь исполнитель, способный к реализации предложенной ему последовательности действий.
Следует иметь в виду, что развитие компьютерной техники и её программного обеспечения всё более ориентируется на пользователя, который не умеет программировать, но применяет компьютеры для решения своих (учебных или профессиональных) задач. Совершенствование вычислительной техники постепенно освобождает пользователя от многих трудоёмких операций. Использование большей части современных компьютерных технологий уже сегодня не требует от пользователя составления последовательности тех шагов, которые необходимы для достижения результата.
Становление информационного общества повлечёт за собой радикальные изменения в сфере производства и деловой активности людей, а также и во всей социальной сфере. В этом обществе, решающую роль будут играть не вещество и энергия, а информация и научные знания – факторы, которые станут определять перспективы его дальнейшего развития.
Часть1. Программа на языке Turbo Pascal
«Дана целочисленная матрица А размером МхN, где М, N – натуральные числа. Элемент матрицы А[i,j] назовём особым, если все элементы j-ого столбца, расположенные выше него, меньше А[i,j]. Найти количество особых элементов матрицы».
Блок-схема алгоритма представлена на рисунке 1.1, а программа и результаты ее работы в Приложении№ 1.
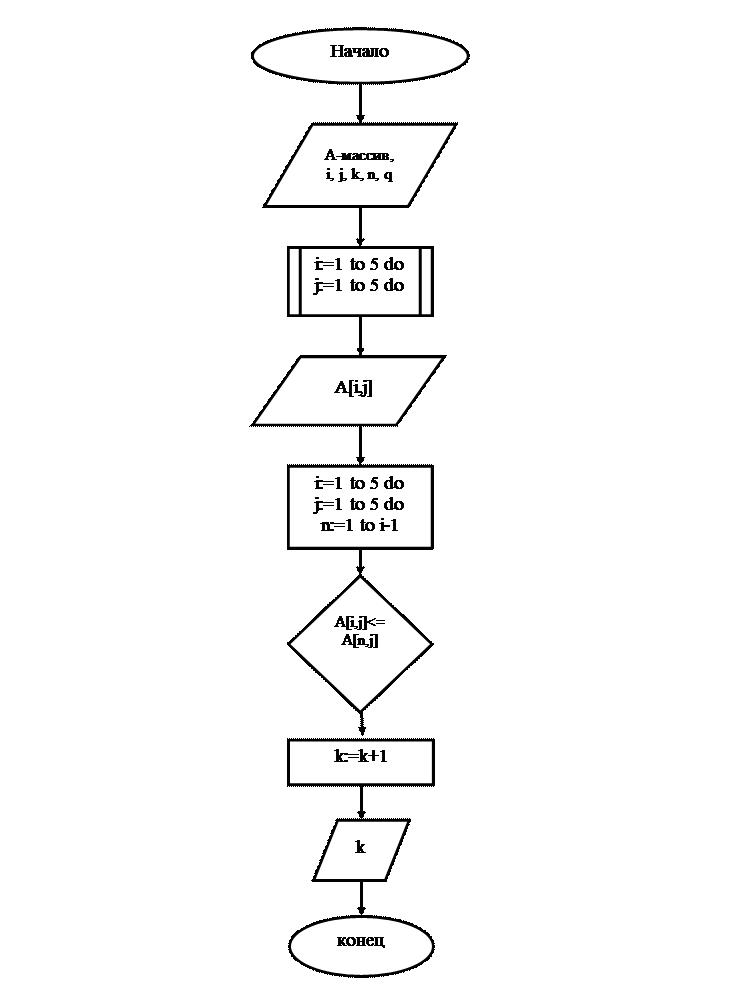рисунок№ 1.1 Блок-схема алгоритма
Часть 2. Рабочая книга Excel
2.1 Лист презентации
Первым листом книги Excel данного курсового проекта является презентация, созданная с помощью стандартных средств Excel (рисунок№ 2.1.1 в Приложении№ 2).
2.2 Лист меню
На втором листе Рабочей книги расположена пользовательская форма с управляющими кнопками (рисунок № 2.2.1 в Приложении№ 2), при нажатии которые осуществляется вызов различных листов Рабочей книги. На каждом листе находятся аналогичные кнопки возврата в основное меню. Все управляющие кнопки созданы с помощью автофигур, путём присоединения к ним макросов, содержащих оператор перехода на указанный лист книги:
Sheets (“Лист N”). Select
Все макросы представлены в Приложении№ 3(рисунок№ 2.2.2)
Решения нелинейного уравнения
Четвертый лист Рабочей книги Excel – решение нелинейного уравнения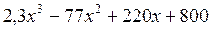 
на промежутке 
.
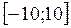При решении данного уравнения графически создана таблица значений функции в точках указанного промежутка, в соответствии с которой построен график с помощью Мастера диаграмм. Решение уравнения также было найдено с помощью команды Подбор параметра (рисунок №2.3.1 в Приложении№ 2).
2.4 Решение системы линейных уравнений.
На пятом листе показано решение системы линейных уравнений
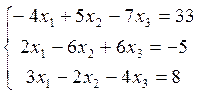
в матричной форме. Неизвестная матрица равна произведению матрицы, обратной данной, на столбец свободных членов. Обратная матрица находится через математическую функцию МОБР, а неизвестная – МУМНОЖ(рисунок № 2.4.1 в Приложении№ 2).
2.5 Решение системы линейных уравнений в MathCAD.
На шестом листе показано решение системы линейных уравнений в MathCad. С помощью встроенных функций находим матрицу, обратную данной, и произведение этой матрицы на столбец свободных членов (рисунок №2.5.1 в Приложении№ 2).
2.6 Решение задачи оптимизации
На данном листе решается задача нахождения экстремума функции при наличии ограничений.
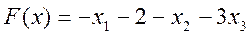
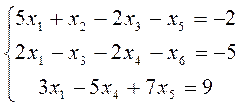
Данная задача представляет собой пример задачи линейного программирования, для решения которой можно воспользоваться опцией Поиск решения.
Определяются значения левых частей уравнений-ограничений. Вводится формула (функция, для которой находится значение). Определяются ячейки со значениями переменных.
В окне Поиск решения заполняются поля:
- целевая ячейка – ячейка с формулой функции;
- изменяемые ячейки – 6 ячеек – x1,x2,x3,x4,x5,x6;
- ограничения: равенство правой и левой частей уравнений-ограничений.
Поиск решения - нажатием кнопки Выполнить – мы получим результат (рисунок № 2.6.1 в Приложении№ 2).