Линейные неоднородные дифференциальные уравнения
с произвольными коэффициентами.
Рассмотрим уравнение вида 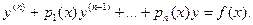
С учетом обозначения 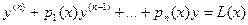 можно записать:
можно записать:
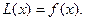
При этом будем полагать, что коэффициенты и правая часть этого уравнения непрерывны на некотором интервале ( конечном или бесконечном).
Теорема. Общее решение линейного неоднородного дифференциального уравнения 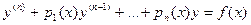 в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.
в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.
Доказательство. Пусть Y – некоторое решение неоднородного уравнения.
Тогда при подстановке этого решения в исходное уравнение получаем тождество:
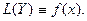
Пусть 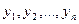 - фундаментальная система решений линейного однородного уравнения
- фундаментальная система решений линейного однородного уравнения 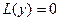 . Тогда общее решение однородного уравнения можно записать в виде:
. Тогда общее решение однородного уравнения можно записать в виде:
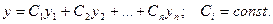
Далее покажем, что сумма 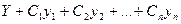 является общим решением неоднородного уравнения.
является общим решением неоднородного уравнения.
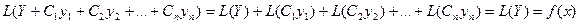

Вообще говоря, решение Y может быть получено из общего решения, т.к. является частным решением.
Таким образом, в соответствии с доказанной теоремой, для решения линейного неоднородного дифференциального уравнения необходимо найти общее решение соответствующего однородного уравнения и каким- то образом отыскать одно частное решение неоднородного уравнения. Обычно оно находится подбором.
На практике удобно применять метод вариации произвольных постоянных.
Для этого сначала находят общее решение соответствующего однородного уравнения в виде:

Затем, полагая коэффициенты Ci функциями от х, ищется решение неоднородного уравнения:
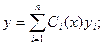
Можно доказать, что для нахождения функций Ci(x) надо решить систему уравнений:
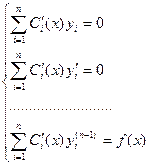
Пример. Решить уравнение 
Решаем линейное однородное уравнение 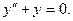
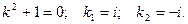
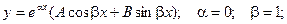
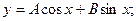
Решение неоднородного уравнения будет иметь вид:
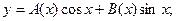
Составляем систему уравнений:
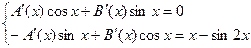
Решим эту систему:
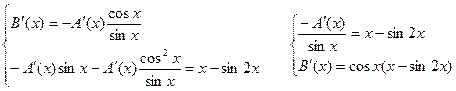
Из соотношения 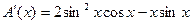 найдем функцию А(х).
найдем функцию А(х).
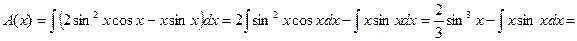
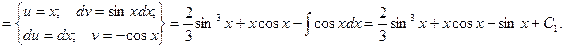
Теперь находим В(х).
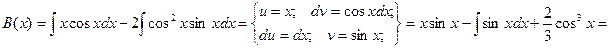
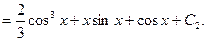
Подставляем полученные значения в формулу общего решения неоднородного уравнения:

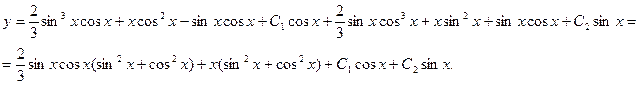
Окончательный ответ: 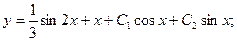
Таким образом, удалось избежать нахождения частного решения неоднородного уравнения методом подбора.
Вообще говоря, метод вариации произвольных постоянных пригоден для нахождения решений любого линейного неоднородного уравнения. Но т.к. нахождение фундаментальной системы решений соответствующего однородного уравнения может быть достаточно сложной задачей, этот метод в основном применяется для неоднородных уравнений с постоянными коэффициентами.
