Формула Ньютона-Лейбница. В соответствии с предыдущим, F(а)=С
В соответствии с предыдущим, F(а)=С. Тогда  Пользуясь этим, можно записать
Пользуясь этим, можно записать  Это центральная формула математического анализа, справедлива для любой непрерывной функции f(t) . Это формула Ньютона-Лейбница.
Это центральная формула математического анализа, справедлива для любой непрерывной функции f(t) . Это формула Ньютона-Лейбница.
16 Замена переменной интегрирования.
Пусть f(х) – интегрируемая функция (Римана), и мы имеем дело вычислением  ( причем а < b) Пусть х= φ(t) – непрерывно дифференцируемая монотонная функция на интервале [α, β] (α<β), причем φ(α)=а, φ(β)=b. Тогда в этих условиях
( причем а < b) Пусть х= φ(t) – непрерывно дифференцируемая монотонная функция на интервале [α, β] (α<β), причем φ(α)=а, φ(β)=b. Тогда в этих условиях 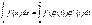 Эта формула немедленно получается учетом того, что F(a)+
Эта формула немедленно получается учетом того, что F(a)+ 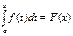
17 Формула интегрирования по частям Можно пользоваться формулой  ибо
ибо 
Простая формула прямоугольников численного интегрмрования
Пусть вычисляется интеграл  Если f(х)≈const на [а,b] , то можно приближенно взять
Если f(х)≈const на [а,b] , то можно приближенно взять  Ошибка порядка
Ошибка порядка 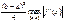 . Это формула прямоугольников.
. Это формула прямоугольников.
Простая формула трапеции численного интегрирования
 , ошибка порядка
, ошибка порядка 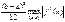 .
.
Простая формула парабол(Симпсона) числ инт
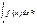

Ошибка интегрирования порядка 
21 по составной формуле прямоугольников имеем 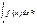
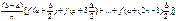
где Δ=(b-а)/n, n-любое натуральное число.
22 По составной формуле трапеций (n-любое натуральное):
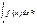

23 По составной формуле Симпсона (n-четное, n=2к)
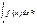

Приложения определенного интеграла.
Длина линии, площадь плоских фигур и площади некоторых поверхностей, объем некоторых тел:
1. Площадьзадача о площади криволинейной трапеции решается с помощью определенного интеграла. В предположении, что эта фигура ограничена сверху линией у= f(х) , имеем (при f(х) >0) 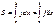 Если линия задана параметрически у= φ(t), х= ψ(t),
Если линия задана параметрически у= φ(t), х= ψ(t), 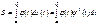
Площадь эллипса: х=аcost, y=bsint; 0<t<π/2; S=1/4 πаb·4= πab
Пусть, далее линия задана уравнением в полярных координатах:
х=r(φ) cos φ у= r(φ) sin φ r= r(φ) – задано
а требуется вычислить площадь сектора , a£j£b. Тогда S≈1/2ΣΔφjrj2=>
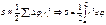 Пример: r=аφ. Это спираль Архимеда . Для нее
Пример: r=аφ. Это спираль Архимеда . Для нее 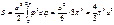
2.Объем тела. Пусть тело, для которого известны площади поперечных сечений, перпендикулярных некоторому направлению, вдоль которого затем задаем координатную ось Х. Итак S(х) – известны. Объем между сечениями в пределах от x=а до x=b:
 Объем тела вращения
Объем тела вращения  y=
y= 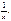
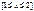 ,
, 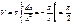 Длина дуги . Пусть линия задана уравнением у= f(х). (Δlj)→0.
Длина дуги . Пусть линия задана уравнением у= f(х). (Δlj)→0.  .. 2 Если линия задана параметрически (x=φ(t), y=ψ(t)) , то получаем
.. 2 Если линия задана параметрически (x=φ(t), y=ψ(t)) , то получаем 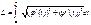 :
:
25 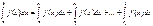 Эта сумма интегралов от непрерывных функций и есть интеграл от разрывной функции с точками разрыва первого рода c1, c2, …,ck.
Эта сумма интегралов от непрерывных функций и есть интеграл от разрывной функции с точками разрыва первого рода c1, c2, …,ck.
Несобственный интеграл по полу- и –бесконечному промежуткам.

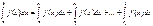
Эта сумма интегралов от непрерывных функций и есть интеграл от разрывной функции с точками разрыва первого рода c1, c2, …,ck.

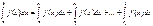
Эта сумма интегралов от непрерывных функций и есть интеграл от разрывной функции с точками разрыва первого рода c1, c2, …,ck.
