Тема 8 Несобственный интеграл
Вычисляется как интеграл с одним или с двумя неограниченными пределами. Подынтегральная функция определена и непрерывна на одном из промежутков [a;+¥), (-¥;b], [-¥;+¥].
Если несобственный интеграл сходится, то он имеет конечный предел, если не сходится, то предел его равен бесконечности (2, с.271, 272).
Для вычисления площадей плоских фигур необходимо уметь определять пределы интегрирования, если они не заданы и если площадь фигуры представляется в виде сумм или разностей криволинейных трапеций. Поэтому нужно построить кривые, ограничивающие плоские фигуры, определяют граничные условия (пределы интегрирования). Необходимо разобрать примеры (1,11.5–11.7, 11.20–11.22, с.300–304, 313), (2, с.261, примеры 11.30–11.35).
Формула трапеций применяется для приближенного вычисления определенного интеграла, когда соответствующая первообразная не вычисляется непосредственным интегрированием.
Разобрать примеры по теме (1, N 11.1–11.11, 11.18–11.22, задачи для самостоятельной работы N 11.25–11.30,11.32–11.35,11.37–11.39, 11.41, 11.42, 11.43–11.52, 11.57, 11.59), (2,11.1 а), б), в), г), д), е), 11.30–11.35, задачи для самостоятельной работы 11.2–11.28, 11.36–11.53, 11.54–11.57, 11.58–11.61, 11.62–11.71, 11.75–11.86).
Тема 9 Дифференциальные уравнения
Понятие о дифференциальных уравнениях. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса. Дифференциальные уравнения первого порядка (неполные, с разделяющимися переменными, однородные и линейные). (1, гл. 12, § 12.1, 12.4–12.7, с. 325–328; 334–340); (2, гл. 2).
Студентам необходимо усвоить определение дифференциального уравнения – как уравнения, которое связывает искомую функцию одной или нескольких переменных и производные различных порядков данной функции.
Дифференциальные уравнения от одной переменной называется обыкновенным дифференциальным уравнением, в дифференциальные уравнения от нескольких переменных – дифференциальные уравнения в частных производных.
Порядок дифференциального уравнения равен порядку старшей степени производной xy¢¢¢-xy¢+5=0 – уравнение третьего порядка.
Нужно помнить, что задача интегрирования дифференциального уравнения – это задача нахождения искомого решения, а график решения называется интегральной кривой.
Общее решение дифференциального уравнения – это решение, которое является функцией переменных х и n произвольных независимых постоянных С1, С2, С0…,Сn.
Частное решение дифференциального уравнения – это решение, полученное из общего при некоторых значениях постоянных.
Для ряда типов дифференциальных уравнений нужно знать студенту основные понятия, нужно уметь решать однородные дифференциальные уравнения, линейные дифференциальные уравнения, неполные дифференциальные уравнения и дифференциальные уравнения с разделяющимися переменными.
Разобрать задачи (1, 12.8–12.22, 12.31–12.32, 12.45–12.47, 12.65). Решить самостоятельно (2, 12.17–12.30, 12.48–12.57, 12.62–12.69, 12.78).
Раздел IVФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Тема 10 Функции нескольких переменных
Функции двух и нескольких переменных. Частные производные и техника дифференцирования. Экстремум функции двух переменных и его необходимое условие. Понятие об эмпирических формулах и методе наименьших квадратов. Построение методом наименьших квадратов линейной функции по эмпирическим данным (вывод системы нормальных уравнений). (1, гл. 15, § 15.1, 15.3, 15.6, 15.8; с. 397–400, 404–406, 410–413); (2, гл. 15).
При изучении этой темы необходимо проводить сравнение с функциями одной переменной и по аналогии определять область определения, но только множеством точек плоскости, а также графики в виде поверхности в пространстве (1, пример 15.2, с.400).
При определении частной производной необходимо использовать понятие частного приращения.
Техника дифференцирования функции двух переменных включает те же правила и принципы, которые использовались для нахождения производных функций одной переменной (1, пример 15.7, 15.8, с.405–406).
Метод наименьших квадратов имеет большое прикладное значение в экономических исследованиях.
Эмпирическая формула включает неизвестные переменные, а критерием ее точности является функция этих параметров, то есть функция нескольких переменных.
Критерий минимизируют, то есть находят экстремум функции нескольких переменных, получают с помощью метода наименьших квадратов формулу, которая является приближением с заданной точностью таблично заданной функции (1, пример 15.11), (2, с.363 –368).
Необходимо обратить внимание на оценку погрешности приближения.
Разобрать задачи с решениями (1, N15.7, 15.9, 15.13) , для самостоятельного решения (1, N 15.23–15.32, 15.39).
Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий
| Начальная буква фамилии | Вариант задания |
| А, Е, Л | Первый |
| Р, Х, Э | Второй |
| Б, Ж, М | Третий |
| С, Ц, Ю | Четвертый |
| В, З, Н | Пятый |
| Т, Ч | Шестой |
| Г, И, О | Седьмой |
| У, Ш | Восьмой |
| Д, К, П | Девятый |
| Ф, Щ, Я | Десятый |
ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
ВАРИАНТ №1
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2.
2.
Задание № 3. Решить задачу:Найти уравнение касательной, проведенной к графику функции у = х3-3х + 5 в точке х0 = 2.
Задание № 4. Исследовать функцию с помощью производных и построить график:
у=2х3 + 3х2 + 1
Задание № 5. Найти интегралы:


Задание № 6. Найти точки экстремума функции нескольких переменных:
z = х2 +ху + у2 – 2х – 3у.
Задание № 7. Выполнить чертеж и решить задачу:Найти объем тела, ограниченного поверхностями:
z = х2 +ху + у2 – 2х – 3у,
z=6.
Задание № 8. Решить дифференциальное уравнение:
х2dу = у2dх, если при х = 1; у = 1.
ВАРИАНТ №2
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2.
2. 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график: 
Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями:
z=7,

Задание № 8 Решить дифференциальное уравнение:

ВАРИАНТ №3
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2
2 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график: 
Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями:

 , z=0.
, z=0.
Задание № 8 Решить дифференциальное уравнение:

ВАРИАНТ №4
Задание № 1 Вычислить пределы: 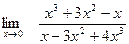 ;
; 
Задание № 2 Найти производные функций:
1.  2.
2. 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график:

Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями:
 , z=0,
, z=0,

Задание № 8 Решить дифференциальное уравнение:

ВАРИАНТ №5
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2.
2. 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график:

Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями:
z=0

Задание № 8 Решить дифференциальное уравнение:

ВАРИАНТ №6
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2.
2. 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график:

Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями:
 , z=0, z=x+2y-5
, z=0, z=x+2y-5
Задание № 8 Решить дифференциальное уравнение:

ВАРИАНТ №7
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2.
2. 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график:

Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями:  .
.
Задание № 8 Решить дифференциальное уравнение: 
ВАРИАНТ №8
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2.
2. 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график:

Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями: z=0,

Задание № 8 Решить дифференциальное уравнение:

ВАРИАНТ №9
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2.
2. 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график:

Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями:

Задание № 8 Решить дифференциальное уравнение:

ВАРИАНТ №10
Задание № 1 Вычислить пределы:  ;
; 
Задание № 2 Найти производные функций:
1.  2.
2. 
Задание № 3 Решить задачу:Найти уравнение касательной, проведенной к графику функции  в точке
в точке  .
. 
Задание № 4 Исследовать функцию с помощью производных и построить график:

Задание № 5 Найти интегралы:
1.  2.
2. 
Задание № 6 Найти точки экстремума функции нескольких переменных:

Задание № 7 Выполнить чертеж и решить задачу: Найти объем тела, ограниченного поверхностями:

Задание № 8 Решить дифференциальное уравнение:

РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
1. Кремер, Н.Ш. Высшая математика для экономистов / Н.Ш.Кремер – М.: Банки и биржи, ЮНИТИ, 1997.
2. Кремер, Н.Ш. Практикум по высшей математике для экономистов / Н.Ш.Кремер – М.: ЮНИТИ-ДАНА, 2002.
3. Зайцев, И.А. Высшая математика / И.А.Зайцев – М.: Высшая школа, 1998.
4. Математический анализ и линейная алгебра. Учебно–методическое пособие / Под ред. Н.Ш.Кремера. – М.: ВЗФЭИ, 2002.
