Уравнения с разделяющимися переменными. где h(y) отлична от нуля всюду на области В, g(x) - определена и непрерывна в В называется
Уравнение
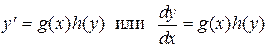 , (6)
, (6)
где h(y) отлична от нуля всюду на области В, g(x) - определена и непрерывна в В называется уравнением с разделяющимися переменными. Деля обе части на h(y) и умножая на dx, получим равенство двух дифференциалов
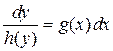 . (7)
. (7)
Из равенства дифференциалов следует, что их неопределенные интегралы отличаются лишь произвольным постоянным слагаемым,
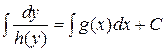 . (8)
. (8)
Уравнение, записанное в виде
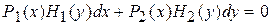 , (9)
, (9)
допускающие выбор в качестве неизвестной функции как у, так и х, решается методом разделения переменных. Общий интеграл уравнения (9) имеет вид
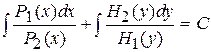 . (10)
. (10)
Пример 1. Решить уравнение
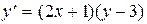 .
.
Интегрируем его для у ¹ 3
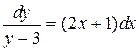 .
.
Его решение представляет собой функцию
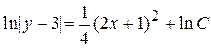 .
.
Прямая у = 3 - частное решение. С учетом проведенных рассуждений общее решение можно переписать в виде
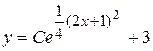 .
.
Если в уравнении (6) g(х) разрывна в некоторой точке х = x и обращается в бесконечность именно в этой точке, а во всех других точках заданной области непрерывна, то решение (8) соответствует общему решению в каждой точке множества 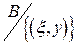 . В точках (x, у) решение определяется из перевернутого уравнения
. В точках (x, у) решение определяется из перевернутого уравнения
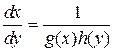
и присоединяется к решению уравнения (6).
Это решение может оказаться особым, если в каждой его точке нарушается единственность или если единственность сохраняется во всех точках этого решения, то оно является частным.
Пример 2. Уравнение 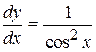 при
при 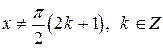 правая часть определена и непрерывна, поэтому формула
правая часть определена и непрерывна, поэтому формула
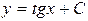
дает общее решение. Прямые 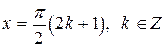 является решением перевернутого уравнения
является решением перевернутого уравнения
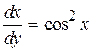 ,
,
причем частным решением и асимптотами общего решения исходного уравнения.
Однородные уравнения
Функция f(x,y) называется однородной степени п, если справедливо равенство
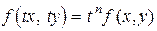 . (11)
. (11)
Дифференциальное уравнение 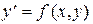 называется однородным, если его правая часть - однородная функция нулевого порядка.
называется однородным, если его правая часть - однородная функция нулевого порядка.
Однородное уравнение можно преобразовать в уравнение с разделяющимися переменными. Выбрав 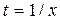 , функция f(x,y) = f(1,y/х). Сохраняя прежнюю независимую переменную х, введем новую искомую функцию u = y/х, откуда
, функция f(x,y) = f(1,y/х). Сохраняя прежнюю независимую переменную х, введем новую искомую функцию u = y/х, откуда 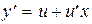 . Тогда исходное уравнение преобразуется в уравнение, допускающее разделение переменных
. Тогда исходное уравнение преобразуется в уравнение, допускающее разделение переменных
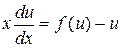 . (12)
. (12)
Если рассмотреть преобразование подобия плоскости с центром подобия в точке (0,0):
х1 = kx, у1 = ky (k > 0). (13)
Это преобразование не изменит вид уравнения (12) (с учетом, что и = у/х), то есть преобразование (13) не меняет всей совокупности решений уравнения. Таким образом, все интегральные кривые однородного уравнения могут быть получены из одной кривой при помощи преобразования подобия с центром подобия в начале координат.
Дифференциальные уравнения вида
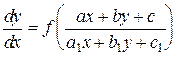 (14)
(14)
приводятся к однородным уравнениям подстановкой вместо х и у новых переменных x и h:
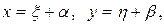 (15)
(15)
где a и b - постоянные, которые определяются так, чтобы числитель и знаменатель преобразованного уравнения не содержал свободных членов. a и b определяются из системы
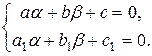 (16)
(16)
Это возможно, если
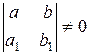 . (17)
. (17)
В этом случае уравнение (14) преобразуется к однородному
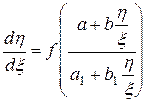 .
.
Если условие (17) не выполняется, то имеет место пропорциональность 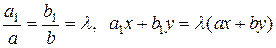 . Вводя новую функцию и вместо у в уравнение (14)
. Вводя новую функцию и вместо у в уравнение (14)
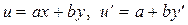 , (18)
, (18)
получим уравнение с разделяющимися переменными
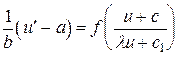 .
.
 М1М М1М |
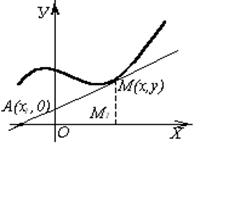
Пример 1. Найти кривые, у которых подкасательная равна сумме абсциссы и ординаты точки касания.
По условию отрезок проекции касательной АМ на ось ОХ равен АМ1 (рис. 4). Тогда
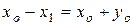 . (19)
. (19)
Точка А (х1, 0) удовлетворяет уравнению касательной к кривой  , тогда
, тогда 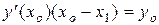 . С учетом формулы (19) получаем дифференциальное уравнение
. С учетом формулы (19) получаем дифференциальное уравнение
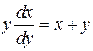 . (20)
. (20)
Полученное уравнение является однородным. Введя новую переменную
z = x/у, 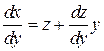 получаем уравнение с разделяющимися переменными
получаем уравнение с разделяющимися переменными 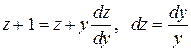 . Интегрируя обе части равенства, получим
. Интегрируя обе части равенства, получим
ln Су = z. Возвращаясь к прежней переменной, получим решение
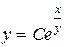 .
.
Пример 2. Решить уравнение
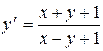 .
.
Так как определитель правой части отличен от нуля, то чтобы свести уравнение к однородному, перенесем начало координат в точку с координатами (a,b), то есть заменим 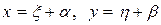 . Подставляя в исходное уравнение, получим
. Подставляя в исходное уравнение, получим
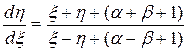 . (21)
. (21)
Подбираем числа a и b так, чтобы
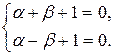 (22)
(22)
Это возможно, т.к. определитель системы (22) отличен от нуля a = -1,
b = 0.
Пусть и = h/x и 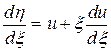 , тогда (21) примет вид
, тогда (21) примет вид
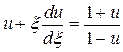 .
.
Разделяя переменные 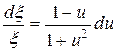 и интегрируя, получим
и интегрируя, получим
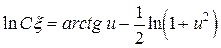 .
.
С учетом вновь введенных переменных общее решение уравнения перепишем так:
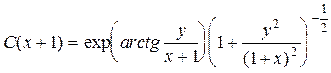 .
.
Некоторые уравнения можно привести к однородным заменой 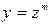 (число m заранее неизвестно). Чтобы его найти, надо в уравнении сделать замену переменной
(число m заранее неизвестно). Чтобы его найти, надо в уравнении сделать замену переменной
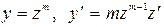
и потребовать, чтобы уравнение стало однородным. Это не всегда возможно, т.к. на одно число m составляется переопределенная система.
Если же такого m найти нельзя, то уравнение не приводится к однородному.
Пример 3. Приведем уравнение 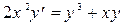 к однородному. После замены
к однородному. После замены 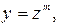 получаем уравнение вида:
получаем уравнение вида:
