Неопределенный интеграл. Интегрирование по частям
Вычислить интегралы с помощью интегрирования по частям:
499. 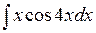 . . | 500. 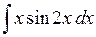 . . | 501. 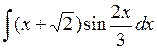 . . |
502. 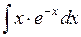 . . | 503. 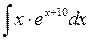 .. .. | 504. 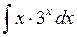 . . |
505. 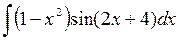 . . | 506. 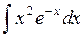 . . | 507. 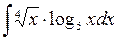 . . |
508. 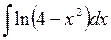 . . | 509. 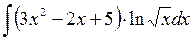 . . | |
510. 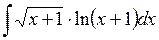 . . | 511. 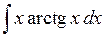 . . | 512. 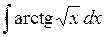 . . |
513. 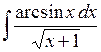 . . | 514. 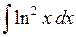 . . | 515. 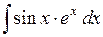 . . |
516. 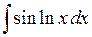 . . | 517. 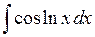 . . |
Ответы.499. 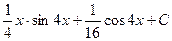 . 500.
. 500. 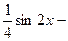
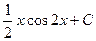 .
.
501. 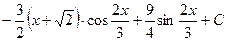 . 502.
. 502. 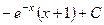 . 503.
. 503. 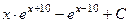 .
.
504. 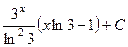 . 505.
. 505. 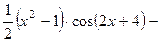
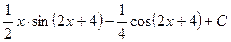 .
.
506. 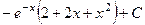 . 507.
. 507. 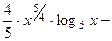
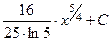 . 508.
. 508. 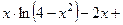
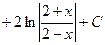 .509.
.509. 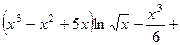
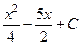 . 510.
. 510. 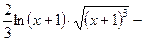
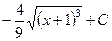 .511.
.511. 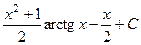 . 512.
. 512. 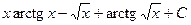 .
.
513. 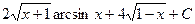 . 514.
. 514. 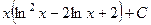 . 515.
. 515. 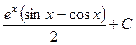 .
.
516. 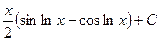 . 517.
. 517. 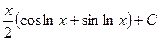 .
.
Неопределенный интеграл. Интегрирование дробно-рациональных функций
Разложить на сумму простейших дробей, не вычисляя коэффициенты:
518. 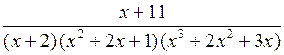 . . | 519. 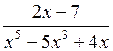 . . |
520. 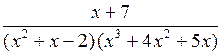 . . | 521. 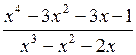 . . |
Вычислить интегралы:
522. 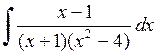 . . | 523. 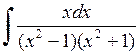 . . | 524. 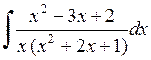 . . |
525. 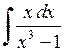 . . | 526. 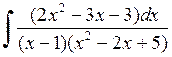 . . | 527. 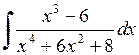 . . |
528. 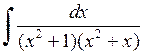 . . | 529. 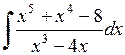 . . | 530. 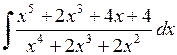 . . |
Ответы.518. 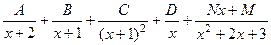 . 519.
. 519. 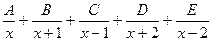 .
.
520. 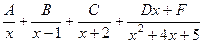 . 521.
. 521. 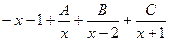 . 522.
. 522. 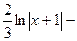
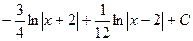 . 523.
. 523. 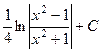 . 524.
. 524. 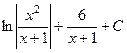 .
.
525. 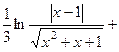
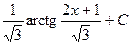 . 526.
. 526. 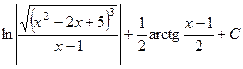 .
.
527. 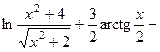
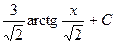 . 528.
. 528. 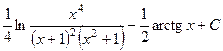 .
.
529. 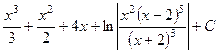 . 530.
. 530. 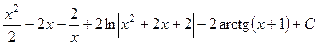 .
.
Неопределенный интеграл. Интегрирование тригонометрических функций
Вычислить интегралы от тригонометрических функций:
531. 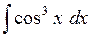 . . | 532. 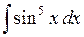 . . | 533. 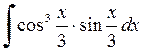 . . |
534. 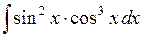 . . | 535. 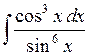 . . | 536. 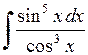 . . |
537. 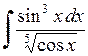 . . | 538. 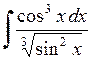 . . |
Вычислить интегралы от тригонометрических функций, используя формулы понижения степени:
539. 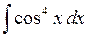 . 540.
. 540. 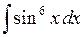 . 541.
. 541. 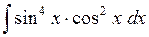 .
.
542. 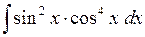 . 543.
. 543. 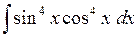 . 544.
. 544. 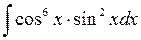 .
.
Вычислить интегралы от тригонометрических функций, приведя подынтегральную функцию к 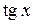 или
или 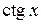 :
:
545. 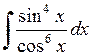 . . | 546. 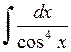 . . | 547. 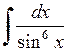 . . | 548. 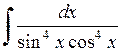 . . |
Вычислить интегралы от тригонометрических функций, используя формулы произведения тригонометрических функций:
549. 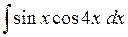 . . | 550. 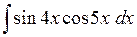 . . | 551. 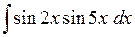 . . |
552. 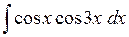 . . | 553. 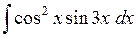 . . | 554. 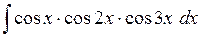 . . |
Вычислить интегралы от тригонометрических функций с помощью замены переменных 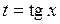 или
или 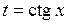 :
:
555. 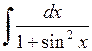 . . | 556. 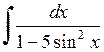 . . | 557. 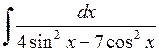 . . |
558. 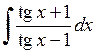 . . | 559. 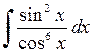 . . | 560. 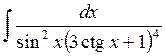 . . |
Вычислить интегралы от тригонометрических функций, используя универсальную тригонометрическую подстановку:
561. 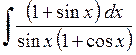 . . | 562. 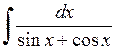 . . | 563. 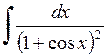 . . |
564. 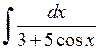 . . | 565. 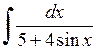 . . | 566. 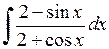 . . |
Ответы. 531. 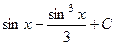 . 532.
. 532. 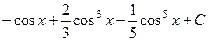 . 533.
. 533. 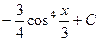 .
.
534. 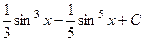 . 535.
. 535. 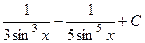 . 536.
. 536. 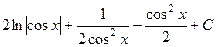 .
.
537. 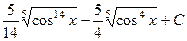 . 538.
. 538. 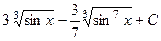 . 539.
. 539. 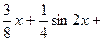
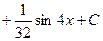 . 540.
. 540. 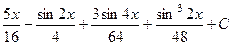 . 541.
. 541. 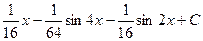 .
.
542. 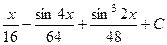 . 543.
. 543. 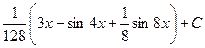 . 544.
. 544. 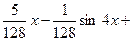
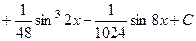 . 545.
. 545. 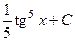 . 546.
. 546. 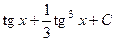 . 547.
. 547. 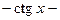
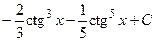 . 548.
. 548. 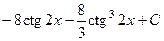 . 549.
. 549. 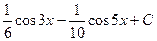 .
.
550. 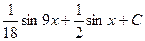 . 551.
. 551. 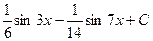 . 552.
. 552. 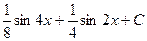 .
.
553. 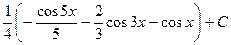 . 554.
. 554. 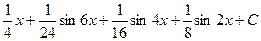 .
.
555. 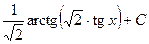 . 556.
. 556. 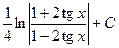 . 557.
. 557. 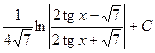 .
.
558. 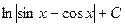 . 559.
. 559. 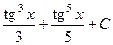 . 560.
. 560. 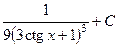 . 561.
. 561. 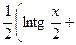
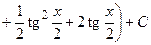 . 562.
. 562. 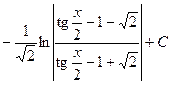 . 563.
. 563. 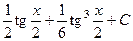 .
.
564. 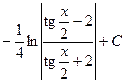 . 565.
. 565. 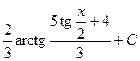 . 566.
. 566. 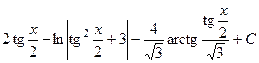 .
.
Неопределенный интеграл. Интегрирование иррациональных функций
Вычислить интегралы от иррациональных функций:
567. 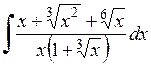 . 568.
. 568. 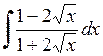 . 569.
. 569. 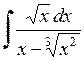 .
.
570. 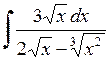 . 571.
. 571. 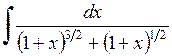 . 572.
. 572. 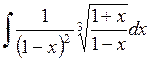 .
.
573. 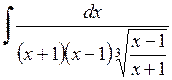 . 574.
. 574. 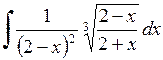 . 575.
. 575. 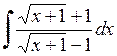 .
.
576. 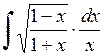 . 577.
. 577. 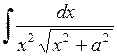 . 578.
. 578. 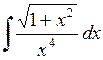 .
.
579. 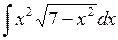 . 580.
. 580. 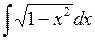 . 581.
. 581. 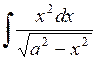 .
.
582. 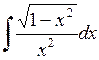 . 583.
. 583. 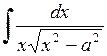 . 584.
. 584. 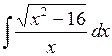 .
.
Ответы. 567. 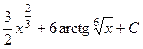 . 568.
. 568. 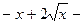
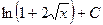 . 569.
. 569. 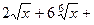
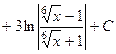 . 570.
. 570. 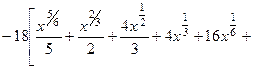
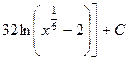 .
.
571. 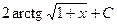 . 572.
. 572. 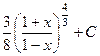 . 573.
. 573. 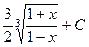 . 574.
. 574. 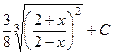 .
.
575. 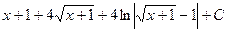 . 576.
. 576. 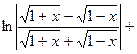
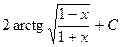 .
.
577. 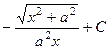 . 578.
. 578. 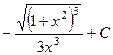 . 579.
. 579. 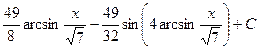 .
.
580. 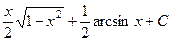 . 581.
. 581. 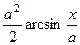
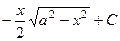 . 582.
. 582. 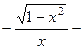
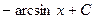 . 583.
. 583. 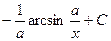 . 584.
. 584. 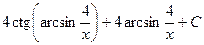 .
.
Определенный интеграл
Вычислить определенные интегралы:
585. 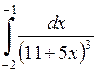 . . | 586. 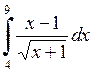 . . | 587. 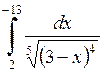 . . |
588. 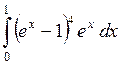 . . | 589. 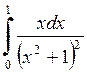 . . | 590. 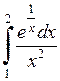 . . |
591. 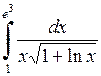 . . | 592. 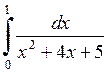 . . | 593. 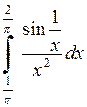 . . |
594. 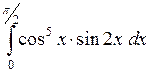 . . |
Вычислить определенные интегралы с помощью замены переменной:
595. 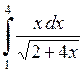 . . | 596. 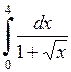 . . | 597. 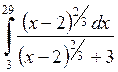 . . |
598. 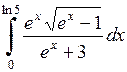 . . | 599. 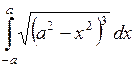 . . | 600. 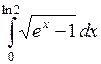 . . |
Вычислить определенные интегралы с помощью интегрирования по частям:
601. 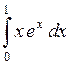 . . | 602. 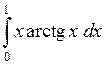 . . | 603. 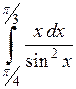 . . |
604. 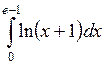 . . | 605. 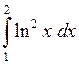 . . |
Ответы.585. 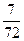 . 586.
. 586. 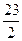 . 587.
. 587. 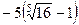 . 588.
. 588. 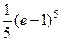 . 589.
. 589. 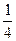 . 590.
. 590. 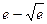 .
.
591. 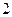 . 592.
. 592. 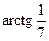 . 593.
. 593. 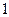 . 594.
. 594. 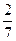 . 595.
. 595. 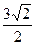 . 596.
. 596. 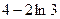 . 597.
. 597. 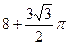 .
.
598. 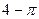 . 599.
. 599. 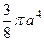 . 600.
. 600. 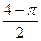 . 601. 1. 602.
. 601. 1. 602. 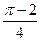 . 603.
. 603. 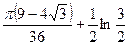 .
.
604. 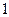 . 605.
. 605. 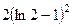 .
.
Приложения определенного интеграла
606.-615. Вычислить площадь фигуры, ограниченной линиями:
606. 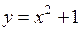 , , 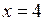 , , 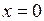 , , 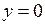 . . | 607. 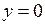 , , 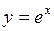 , , 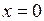 , , 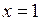 . . |
608. 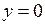 , , 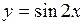 , , 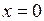 , , 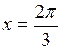 . . | 609. 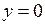 , , 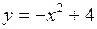 , , 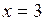 . . |
610. 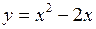 , , 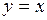 . . | 611. 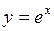 , , 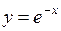 , , 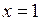 . . |
612. 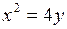 , , 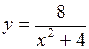 . . | 613. 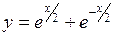 , , 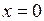 , , 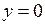 , , 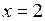 . . |
614. 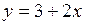 , , 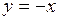 , , 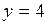 . . | 615. 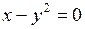 , , 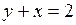 . . |
616. Вычислить площадь фигуры, содержащейся внутри кардиоиды
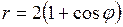 .
.
617. Вычислить площадь фигуры, ограниченной одним завитком кривой
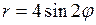 .
.
618. Вычислить площадь одной петли кривой 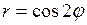 .
.
619. Вычислить площадь эллипса 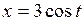 ,
, 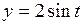 .
.
620. Найти площадь фигуры, ограниченной кривой 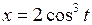 ,
, 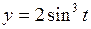 .
.
621. Найти длину дуги кривой 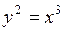 от
от 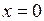 до
до 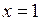
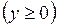 .
.
622. Найти длину дуги кривой 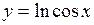 от
от 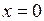 до
до 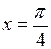 .
.
623. Найти длину дуги кривой 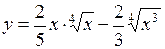 между точками пересечения с осью
между точками пересечения с осью 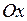 .
.
624. Найти длину дуги цепной линии 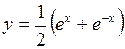 от
от 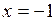 до
до 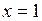 .
.
625. Найти длину дуги 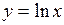 от
от 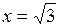 до
до 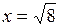 .
.
626. Найти длину дуги кривой 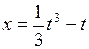 ,
, 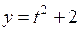 от
от 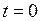 до
до 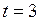 .
.
627. Вычислить длину дуги кривой 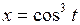 ,
, 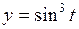 , если
, если 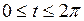 .
.
628. Вычислить длину дуги циклоиды 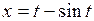 ,
, 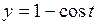 .
.
629.Вычислить объем тела, образованного вращением эллипса 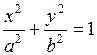 вокруг оси
вокруг оси 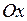 .
.
630.Вычислить объем тела, образованного вращением вокруг оси 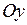 площади, ограниченной линиями:
площади, ограниченной линиями: 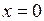 ,
, 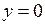 ,
, 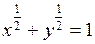 .
.
631.Вычислить объем тела, образованного вращением вокруг оси 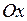 площади, ограниченной линиями:
площади, ограниченной линиями: 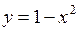 ,
, 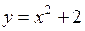 ,
, 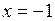 ,
, 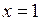 .
.
632.Вычислить объем тела, образованного вращением вокруг оси 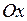 площади, ограниченной линиями:
площади, ограниченной линиями: 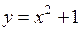 ,
, 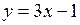 .
.
633.Вычислить объем тела, образованного вращением вокруг оси 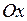 площади, ограниченной линиями:
площади, ограниченной линиями: 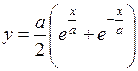 ,
, 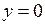 ,
, 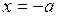 ,
, 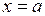 .
.
634.Найти объем конуса, полученного вращением вокруг оси 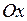 части прямой
части прямой 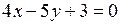 , содержащейся между осями координат.
, содержащейся между осями координат.
Ответы. 606. 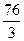 . 607.
. 607. 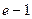 . 608.
. 608. 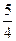 . 609. 13. 610.
. 609. 13. 610. 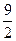 . 611.
. 611. 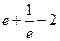 .
.
612. 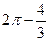 . 613.
. 613. 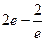 . 614.
. 614. 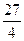 . 615.
. 615. 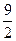 . 616.
. 616. 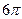 . 617.
. 617. 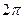 . 618.
. 618. 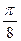 .
.
619. 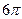 . 620.
. 620. 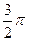 . 621.
. 621. 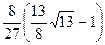 . 622.
. 622. 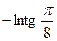 . 623.
. 623. 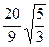 . 624.
. 624. 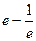 .
.
625. 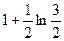 . 626.
. 626. 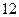 . 627.
. 627. 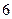 . 628.
. 628. 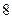 . 629.
. 629. 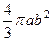 . 630.
. 630. 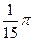 . 631.
. 631. 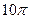 .
.
632. 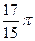 . 633.
. 633. 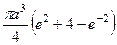 . 634.
. 634. 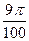 .
.
