Методика выполнения работы

Знакомство с интерфейсом MATLAB и начало работы.

1. Запустите систему MATLAB, щелкнув дважды по иконке на рабочем столе. Появляется основное окно MATLAB (рисунок 1). Изменить вид окна можно во вкладке Вид. Для получения вида, представленного на рис.1, необходимо проставить «галочки» в меню «Вид» (View) напротив Окно команд (Command Window), Команды (Command History), Рабочая область (Workspace).

В Окне команд (Command Window) осуществляется ввод матриц, векторов, переменных, формул, команд. В окне Команды (Command History отображается «история» введенных команд. В Рабочей области (Workspace) отображаются результаты ввода и расчеты, значения всех использованных переменных, матриц и векторов. Существует ряд основных команд управления Окном командного режима (Command Window):

· clс — очищает экран и размещает курсор в левом верхнем углу пустого экрана.

· home — возвращает курсор в левый верхний угол окна.

· mоrе on — включает режим постраничного вывода (полезен при просмотре больших m-файлов).

· mоrе off — отключает режим постраничного вывода (в этом случае для просмотра больших фалов надо пользоваться линейкой прокрутки).

Команды clc и home действуют аналогично — очищают экран и помещают курсор в левый верхний угол окна командного режима работы.

В системе MATLAB можно задавать переменным определенные значения. Для этого используется операция присваивания, вводимая знаком равенства =

Имя_переменной = Выражение

Типы переменных заранее не декларируются. Они определяются выражением, значение которого присваивается переменной. Так, если это выражение — вектор или матрица, то переменная будет векторной или матричной.

Имя переменной (ее идентификатор) может содержать сколько угодно символов, но запоминается и идентифицируется только 31 начальный символ. Имя любой переменной не должно совпадать с именами других переменных, функций и процедур системы, т. е. оно должно быть уникальным. Имя должно начинаться с буквы, может содержать буквы, цифры и символ подчеркивания _. Недопустимо включать в имена переменных пробелы и специальные знаки, например +,.-, *, / и т. д., поскольку в этом случае правильная интерпретация выражений становится невозможной.

Существует ряд основных правил для общения с MATLAB:

· для указания ввода исходных данных используется символ >>;

· данные вводятся с помощью простейшего строчного редактора;

· для блокировки вывода результата вычислений некоторого выражения после него надо установить знак ; (точка с запятой);

· если не указана переменная для значения результата вычислений, то MATLAB назначает такую переменную с именем ans;

· знаком присваивания является привычный математикам знак равенства =, а не комбинированный знак :=, как во многих других языках программирования и математических системах;

· результат вычислений выводится в строках вывода (без знака »);

· встроенные функции (например, sin) записываются строчными буквами, и их аргументы указываются в круглых скобках;

· диалог происходит в стиле «задал вопрос — получил ответ».

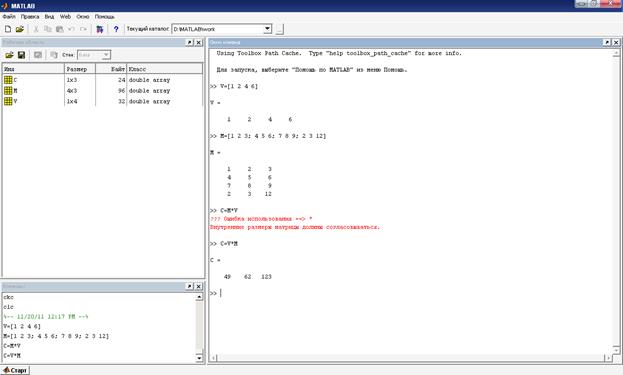
Рисунок 1 – Основное окно системы MATLAB

2. Введите матрицу и вектор. При вводе строки матрицы или вектора между элементами строки ставится пробел или запятая, строки отделяются друг от друга точкой с запятой (рис.1).

Задать четырехэлементный вектор-строку V со значениями элементов 1, 2, 3 и 4. Записи вводятся в Окне команд после символа >>, который устанавливается автоматически. Две записи для вектора — V=[l 2 3 4] и V=[1,2,3.4] — являются идентичными. Список заключается в квадратные скобки. После ввода вектора нажать Enter. В Окне команд (Command Window) появляется запись введенного вектора:

V =

1 2 3 4

В Рабочей области (Workspace) (слева) появляется запись об имени и размере введенного вектора V. Щелкнув левой кнопкой мыши на эту запись, можно раскрыть ее и увидеть содержимое введенного вектора. Для выделения п-го элемента вектора V используется выражение V(n). Оно задает соответствующую индексированную переменную.

Задать матрицу М размерностью 4х3

.

Для этого в Окне команд ввести

>> M=[1 2 3; 4 5 6; 7 8 9; 2 3 12] и нажать Enter.

В результате в Рабочей области (Workspace) появляется запись о введенной матрице M, а в Окне команд появляется результат ввода (рис. 1):

M =

1 2 3

4 5 6

7 8 9

2 3 12

Для выделения отдельного элемента матрицы М используется выражение вида M(j,i), где М — имя матрицы, j — номер строки и i — номер столбца.

3. Ознакомьтесь с правилами использования операторов и функций.

Оператор — это специальное обозначение для определенной операции над данными — операндами. Используются следующие операторы:

+ сложение;

- вычитание;

* умножение;

.* поэлементное умножение массивов;

/ деление;

./ поэлементное деление массивов;

\ левое деление (деление справа налево);

^ возведение в степень;

‘ транспонирование

( ) определение порядка вычислений.

Система MATLAB предоставляет большое количество элементарных математических функций, а также логических функций, функций обработки множеств и т.д. Несколько специальных функций представляют значения часто используемых констант:

аns – результат выполнения последней операции;

pi – 3.14159265…;

i или j – мнимая единица ( );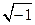

eps – относительная точность числа с плавающей точкой, 2^-52;

realmin – наименьшее число с плавающей точкой, 2^-1022;

realmax – наибольшее число с плавающей точкой, ;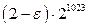

Inf – бесконечность;

NAN – не число.

Имена функций не являются зарезервированными, поэтому возможно изменять их значения на новые. В системе MATLAB определены следующие функции:

Таблица 1. – Основные функции

Функция	Название	Пример
Математические
abs(X)	Модуль. Возвращает абсолютную величину для каждого числового элемента вектора X.	>> abs(-5) ans =
ехр(Х)	Экспонента. Возвращает экспоненту для каждого элемента X.	>> ехр([1 2 3]) ans = 2.7183 7.3891 20.0855
inv(A)	Возвращает матрицу А-1, обратную матрице А	A = 1 1 1 0 1 -1 3 1 -1 2 0 3 3 1 1 -1 >> inv(A) ans = -1.000 0.100 0.200 0.700 1.000 -0.250 0 -0.2500 1.000 0.150 -0.200 -0.450 -1.000 0.200 0.400 0.400
det(A)	Возвращает определитель матрицы А	A = 1 1 1 0 1 -1 3 1 -1 2 0 3 3 1 1 -1 >> det(A) ans = -20
log(X)	Возвращает натуральный логарифм элементов массива X.	>> Х=[1.2 3.34 5 2.3]; >> log(X) ans= -0.1823 1.2060 1.6094 0.8329
log2(X)	Возвращает логарифм по основанию 2 элементов массива X.	>> X=[1.2 3.34 5 2.3]; >> log2(X) ans = 0.2630 1.7398 2.3219 1.2016
log10(X)	Возвращает логарифм по основанию 10 элементов массива X.	>> X=[1.2 3.34 5 2.3]; >> log10(X) ans = 0.0792 0.5237 0.6990 0.3617
sqrt(X)	Возвращает квадратный корень каждого элемента массива X	>> А=[25 21.23 55.8 3]: >> sqrt(A) ans = 5.0 4.6076 7.4699 1.7321
cos(X)	Возвращает косинус для каждого элемента X	>> X=[1 2 3]; >> cos(X) ans = 0.5403 -0.4161 -0.9900
acos(X)	Возвращает арккосинус для каждого элемента X	>>Y = acos (0.5) Y= 1.0472
sin(X)	Возвращает синус для каждого элемента X	>> X=[pi/2 pi/4 pi/6 pi]; >> sin(X) ans = 1.000 0.7071 0.500 0.000
asin(X)	Возвращает арксинус для каждого элемента X	>> Y= asin (0.278) Y = 0.2817
tan(X)	Возвращает тангенс для каждого элемента X	>> Х=[0.08 0.06 1.09] >> tan(X) ans= 0.802 0.0601 1.9171
atan(X)	Возвращает арктангенс для каждого элемента X	>> Y=atan(1) Y = 0.7854
mod(X,Y)	Возвращает остаток от дедения X на Y	>> mod(5,2) ans =
Функции и операторы отношения Данные операторы выполняют поэлементное сравнение векторов или матриц одинакового размера и возвращают значение 1 (True), если элементы идентичны, и значение 0 (False) в противном случае.
eq	Равно. Оператор: = =	>> eq(2, 2) ans = >> 2==2 ans =
ne	Не равно. Оператор: ~ =	>> ne(l, 2) ans = >> 2 ~- 2 ans =
Lt	Меньше чем. Оператор: <	x<y
Gt	Больше чем . Оператор: >	x>y
Le	Меньше или равно. Оператор: <=	x<=y
Ge	Больше или равно. Оператор: >=	x>=y
Логические операторы и функции
And	Логическое И (AND) &	»А=[1 2 3]; »В=[1 0 0]; » and(A.B) ans = 1 0 0
Or	Логическое ИЛИ (OR) |	>> оr(А.В) ans = 1 1 1
Not	Логическое НЕ (NOT) ~	>> not(А) ans = 0 0 0 >> not(B) ans = 0 1 1

3. Использование прямых вычислений. Система MATLAB создана таким образом, что любые (подчас весьма сложные) вычисления можно выполнять в режиме прямых вычислений, то есть без подготовки программы. Это превращает MATLAB в необычайно мощный калькулятор, который способен производить не только обычные для калькуляторов вычисления (например, выполнять арифметические операции и вычислять элементарные функции), но и операции с векторами и матрицами, комплексными числами, рядами и полиномами.

Работа с системой в режиме прямых вычислений носит диалоговый характер и происходит по правилу «задал вопрос, получил ответ». Пользователь набирает на клавиатуре вычисляемое выражение, редактирует его (если нужно) в командной строке и завершает ввод нажатием клавиши ENTER.

В качестве примера проведем простейшие вычисления: вычислим произведение введенных ранее вектора V и матрицы М (C=VxM). Очевидно, что результатом должен быть вектор-строка C размерностью 1х3 (обратите внимание, рис.1, что произведение МхV невозможно). В Окне команд наберем >> C=V*M Результат приведен на рис.1.

Самостоятельно проведите простейшие вычисления. Например

>> 2+3 Нажмите Enter. Получим ответ

ans=

>> sin(l)

ans=

0.8415

Вычислим значения синусов элементов матрицы M. Результатом будет матрица МХ, элементами которой будут синусы элементов матрицы М. Для этого введем выражение

>> MX=sin(M)

Вычислите косинусы элементов вектора V.

>> VC=cos(V)

Ознакомьтесь с проведением операций со следующими векторами V1 и V2:

» Vl=[2 4 6 8]

V1=

2 4 6 8

» V2=[l 2 3 4]

V2 =

1 2 3 4

» V1/V2

ans =

» V1.*V2

ans=

2 8 18 32

» V1./V2

ans =

2 2 2 2

3. Решение систем линейных уравнений в режиме прямых вычислений.

Решим систему линейных уравнений:

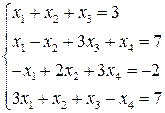
двумя способами – методом Крамера и матричным методом.

Запишем приведенную выше систему в матричной форме

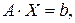
где 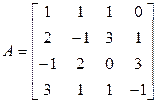– матрица системы; 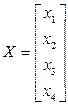– вектор-столбец неизвестных;

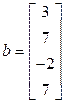– вектор-столбец свободных членов системы.

3.1 Решение методом Крамера.

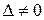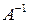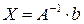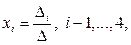Если определитель матрицы А, , т.е. матрица А имеет обратную , то система имеет единственное решение , или где 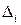– определитель, получаемый из определителя 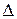матрицы системы заменой i-го столбца на столбец свободных членов.

Ведем матрицу системы А

>> A=[1 1 1 0; 2 -1 3 1; -1 2 0 3; 3 1 1 -1]

A =

1 1 1 0

1 -1 3 1

-1 2 0 3

3 1 1 -1

Вычислим определитель матрицы А, обозначив его D

>> D=det(A)

D =

-20

Введем матрицы A1, A2, A3 и А4, где соответственно 1-й, 2-й, 3-й и 4-й столбец матрицы А заменен столбцом свободных членов системы:

>> A1=[3 1 1 0; 7 -1 3 1; -2 2 0 3; 7 1 1 -1]

A1 =

3 1 1 0

7 -1 3 1

-2 2 0 3

7 1 1 -1

>> A2=[1 3 1 0; 1 7 3 1; -1 -2 0 3; 3 7 1 -1]

A2 =

1 3 1 0

1 7 3 1

-1 -2 0 3

3 7 1 -1

>> A3=[1 1 3 0; 1 -1 7 1; -1 2 -2 3; 3 1 7 -1]

A3 =

1 1 3 0

1 -1 7 1

-1 2 -2 3

3 1 7 -1

>> A4=[1 1 1 3; 1 -1 3 7; -1 2 0 -2; 3 1 1 7]

A4 =

1 1 1 3

1 -1 3 7

-1 2 0 -2

3 1 1 7

Теперь вычислим определители введенных матриц:

>> D1=det(A1)

D1 =

-44

>> D2=det(A2)

D2 =

>> D3=det(A3)

D3 =

-26

>> D4=det(A4)

D4 =

-8

Теперь вычислим корни системы

>> X1=D1/D

X1 =

2.2000

>> X2=D2/D

X2 =

-0.5000

>> X3=D3/D

X3 =

1.3000

>> X4=D4/D

X4 =

0.4000

3.2 Решение матричным методом

MATLAB позволяет решить эту систему с помощью матричного выражения 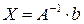, минуя вычисление определителей. Для этого необходимо ввести вектор-столбец свободных членов системы b.

>> A=[1 1 1 0; 1 -1 3 1; -1 2 0 3; 3 1 1 -1]

A =

1 1 1 0

1 -1 3 1

-1 2 0 3

3 1 1 -1

>> b=[3; 7; -2; 7]

b =

-2

>> X=inv(A)*b

X =

2.2000

-0.5000

1.3000

0.4000

Очевидно, что решение системы уравнений матричным методом и методом Крамера дает одни и те же результаты.

4. Создание М-файлов.

Для решения задачи создадим два М-файла – файл-функцию для решения системы уравнений методом Крамера и файл-сценарий, где будут определяться исходные матрицы и вычисляться вектор корней системы,

4.1 Создание файла-функции.

Для создания М-файла на панели инструментов нажмите иконку Новый М-файл (Рисунок 1.1), Либо выполнить команды File – New—M-file.

Рисунок 1.1 – Создание нового М-файла

Открывается окно М-файла. Сюда введите операторы, соответствующие решению системы уравнений методом Крамера. Назовем функцию Kramer. Входными аргументами являются матрица системы А и вектор свободных членов b, выходными – вектор Х. Функция имеет вид, представленный на рис. 2.

После начала выполнения функции рассчитывается определитель матрицы системы А. Затем вводятся новые матрицы А1, А2, А3 и А4, где соответственно 1-й, 2-й, 3-й и 4-й столбцы заменяются столбцом свободных членов b.

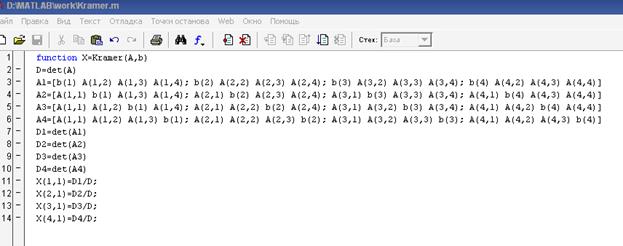
Рисунок 2 – Файл-функция решения системы уравнений методом Крамера

Далее рассчитываются определители новых матриц и элементы вектора корней системы Х. Вектор Х будет представлять из себя вектор-столбец. На это указывает нумерация элементов вектора, где первая цифра номер строки, вторая – номер столбца. Если пронумеровать элементы вектора Х, как Х(1), Х(2), Х(3) и Х(4), то вектор Х будет представлять из себя вектор-строку.

Сохраните файл-функцию под именем Kramer в папке work каталога MATLAB . Для этого нажмите в строке меню Файл (File) – Сохранить как (Save As), либо на Панели инструментов нажмите иконку Сохранить. Появляется окно Сохранить как с содержимым папки work (рис.3). Имя файла должно быть таким же, как и имя функции (Kramer). Нажать Сохранит (Save)ь.

Рисунок 3 – Сохранения М-файла

4.2 Создание файла-сценария.

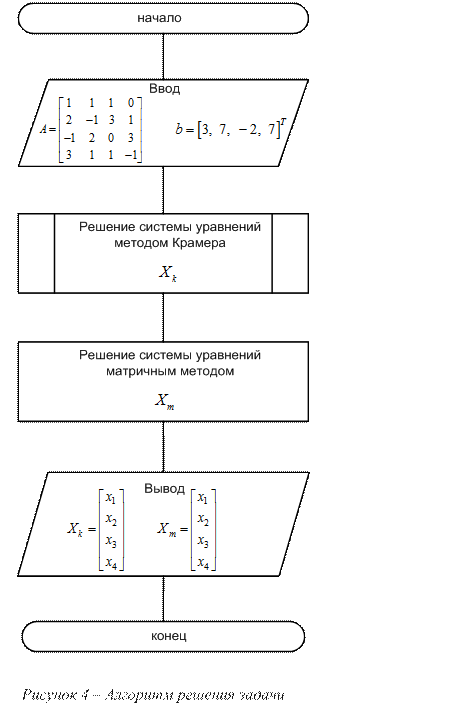
Аналогично пункту 4.1 создайте новый М-файл. Запишите в него программный код, соответствующий решению системы линейных уравнений методом Крамера и матричным методом. Блок-схема алгоритма решения задачи представлена на рис. 4. Предопределенный процесс «Решение системы уравнений методом Крамера» представляет из себя файл-функцию Kramer, введенную ранее.

Соответствующий приведенному на рис.4 алгоритму программный код выглядит следующим образом:

% Решение системы уравнений

A=[1 1 1 0; 1 -1 3 1; -1 2 0 3; 3 1 1 -1]

b=[3; 7; -2; 7]

% Решения методом Крамера

Xk=Kramer(A,b)

% Решение матричным методом

Xm=inv(A)*b

4. Запустите на выполнение файл-сценарий. Для этого в строке меню выберите Отладка (Debug) – Сохранить и запустить (Save and Run). Следует помнить, что на решение запускается именно файл-сценарий, а не файл-функция. Происходит выполнения программы. Результаты отображаются в основном окне MATLAB. В окне команд отображаются результаты выполнения каждой строки программы, где в конце строки не стоит знак «точка с запятой» (;). Это удобно при отладке программ. Если вы не хотите вывода промежуточных результатов, то в конце соответствующей строки программы поставьте знак «точка с запятой».

В Рабочей области окна MATLAB отображаются переменные и массивы, введенные в программу и рассчитанные в ней. В данном случае там будут отображаться матрица А, вектор-столбец b, векторы-столбцы результатов решения системы, методом Крамера – X_k, матричным методом X_m. Щелкнув дважды левой кнопкой мыши по любому массиву или переменной из Рабочей области, можно раскрыть их значения в специальном окне Array Editor: (рис. 5).

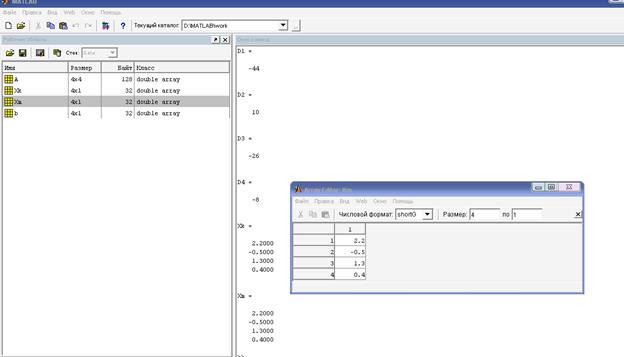
Рисунок 5 – Результаты решения задачи