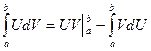Метод интегрирования по частям

Теорема: Пусть функции U(x) и V(x) определены и дифференцируемы, на множестве Х и пусть функция U’(x)*V(x) имеет первообразную на этом промежутке, тогда на Х функция U(x)*V’(x) так же имеет первообразную и справедлива формула: 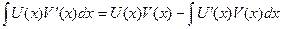. Док-во: [U(x)V(x)]’=U’(x)V(x)+U(x)V’(x) => U(x)V’(x)=-U’(x)V(x)+[U(x)V(x)]’, интегрируя обе части получаем: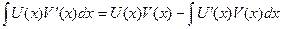

Определённый интеграл (определение, геометрический смысл)

Пусть y=f(x), определена на отрезке [a;b]:

Разобьём этот отрезок на n произвольных частей точками a=x0<x1<x2<…<x_i-1<x_i<…<xn=b, причём отрезки не обязательно равные. На каждом отрезке выберем произвольную точку xiÎ[ x_i-1;x_i], найдём жначение функции f в точке xi. Обозначим Dxi растояние между точками xi и xi-1. найдём соответствующее произведение: f(xi)Dxi. Составим сумму этих произведений:

Сумма такого сида называется интегральной суммой функции y=f(x) на отрезке [a;b]. Обозначим в качестве .

Определние: если существует конечный предел интегральной суммы при l®0, то этот предел называется определёенным интегралом от функции y=f(x) по отрезку [a;b] и обозначается: .

Теорема Коши: Если функция y=f(x) непрерывна на отрезке [a;b], то определённый интеграл существует.

Геометрический смысл: площадь криволинейной трапеции, ограниченной с верху функцией y=f(x), с низу осью Ох, и по бокам прямыми х=а, х=b.

Формула Ньютона-Лейбница.

Если функция y=f(x) непрерывна на [a;b] и F(x) – какая либо первообразная функции на [a;b], т.е. F’(x)=f(x), то имеет место формула: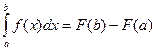

Док-во: рассмотрим разность F(b)-F(a)=F(xn)-F(x0)=[F(x n)-F(x n-1)]+[F(x n-1)-F(x n-2)]+…+[F(x2)-F(x1)]+[F(x1)-F(x0)]. Разложим каждую скобку по формуле Лагранжа: F’(xn)(xn-x n-1)+ F’(x n-1)(x n-1- x n-2)+…+ F’(x2)(x2-x1)+ F’(x1)(x1-x0)=f(xn)Dxn+ f(xn-1)Dxn-1+…+ f(x2)Dx2+ f(x1)Dx1= 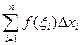- интегральная сумма.

По теореме Коши т.к. функция непрерывна, то определённый интеграл существует. Так .

Основные свойства определённого интеграла

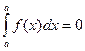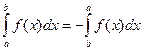1) ; 2) ; 3) ;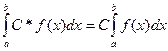

4) ;

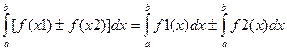5) .

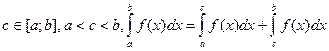6) Теорема о среднем: если функция y=f(x) непрерывна на отрезке [a;b], то . Док-во: 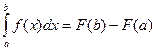=по формуле Ньютона-Лейбница, разложим по формуле Лагранжа= F’(c)(b-a)=f(c)(b-a).

Интеграл с переменным верхним пределом

Рассмотрим интеграл 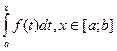. В данном интеграле нижний предел=const, а верхний предел – переменная. Величина этого интеграла является функцией зависящей от верхнего предела х, обозначим её как Ф(х) и этот интеграл назовём Интегралом с переменным верхним пределом.

Теорема Барроу: Производная от непрерывной функции по переменному верхнему пределу существует и равна подынтегральной функции в точке, равной верхнему пределу, т.е. .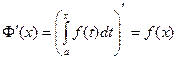

Основные методы интегрирования

1) Непосредственное интегрирование осуществляется по формуле Ньютона-Лейбница.

2) Замена переменной в определённом интеграле:

3) Интегрирование по частям: