Найдем критерии надежности данной системы методом интегральных уравнений

Вероятность безотказной работы системы:

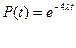
Среднее время безотказной работы :

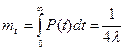
Для заданных значений t = 8760 ч и 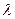= 8∙10^-5 1/ч

P_сист = 0,061

mt(λ=8∙10^-5) = 3,125*10³ ч.

Восстанавливаемая резервированная система с целой кратностью при неограниченном ремонте

Система с нагруженным резервом

Рис. 10. Схема надежности восстанавливаемой резервированной системы с целой кратностью при ограниченном ремонте с нагруженным резервом

На рис. 10 элемент 1 – основной, а элемент 2 - резервный. Резерв является нагруженным, поэтому резервный элемент имеет интенсивность отказов λ. Отказавший элемент может быть восстановлен.

Система будет работоспособной, если хотя бы один из ее элементов работоспособен.

Рис. 11. Вероятностный граф состояний системы

Найдем критерии надежности системы методом дифференциальных уравнений.

На основании вероятностного графа системы, представленного на рис. 11, запишем систему дифференциальных уравнений.

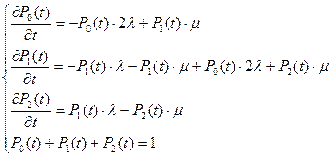Начальные условия:

P₀(0)=1

P₁(0)=0

P₂(0)=0.

Применим преобразование Лапласа к левой и правой частям уравнений полученной системы:

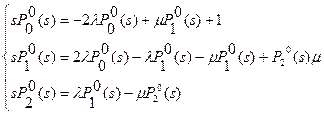
Преобразуем систему:

Представим систему в матричном виде:

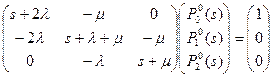Отсюда

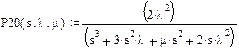
Выполним обратное преобразование Лапласа и подставим заданное значение t=8760 ч:

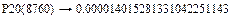
Вероятность безотказной работы: P(t)=1 – P₂(t)

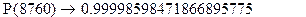
Среднее время безотказной работы определим по формуле

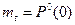, где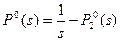

Подставляя выражение для P₂⁰(s), получим:

Подставив значение s=0, получим:

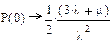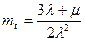
Для определения коэффициента готовности составим по графу состояний систему дифференциальных уравнений с учетом обратного перехода из состояния 2:

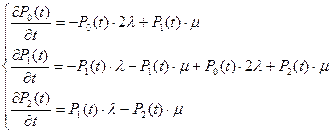При t→∞ система примет следующий вид:

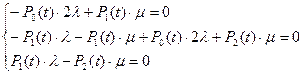
После преобразований система примет вид:

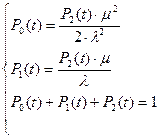
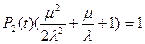
Коэффициент готовности:

K_Г =1 – P₂

Подставляя значение P₂, получим:

K_Г =1 –

Найдем коэффициент готовности данной системы методом Половко.

Запишем вероятности системы по графу, представленному на рис.11:

Коэффициент готовности системы:

,

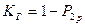
Коэффициент готовности системы, рассчитанный методом Половко, совпал с коэффициентом готовности системы, рассчитанным методом дифференциальных уравнений.

K_Г= 0,99999999980000399996

Среднее время восстановления:

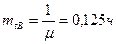
Вероятность успешного использования системы:

R(t)=K_ГP(t)

Система с ненагруженным резервом

Рис. 12. Схема надежности восстанавливаемой резервированной системы с целой кратностью при неограниченном ремонте с

ненагруженным резервом

На рис. 12 элемент 1 – основной, а элемент 2 - резервный. Отказавший элемент может быть восстановлен. Система будет работоспособной, если хотя бы один из ее элементов работоспособен.

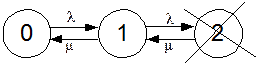Рис. 13. Вероятностный граф состояний системы