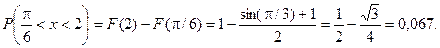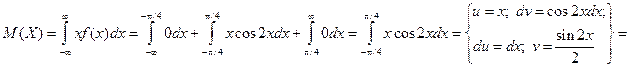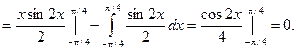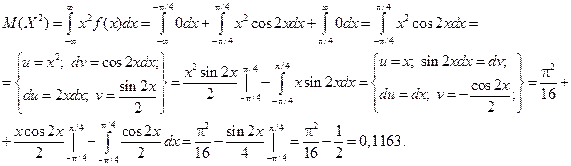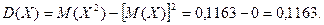Свойства плотности распределения

1) Плотность распределения является неотрицательной функцией:

.

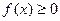2) Несобственный интеграл от плотности распределения в пределах от 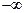до ¥ равен единице:

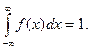
Определение. Математическим ожиданиемнепрерывной случайной величины Х, возможные значения которой принадлежат отрезку 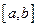, называется определенный интеграл:

.

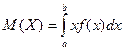Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

.

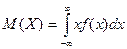При этом, конечно предполагается, что несобственный интеграл сходится.

Определение. Дисперсией непрерывной случайной величины, возможные значения которой принадлежат отрезку 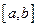, называется математическое ожидание квадрата ее отклонения:

.

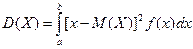Если возможные значения случайной величины рассматриваются на всей числовой оси, то дисперсия находится по формуле:

.

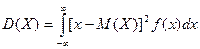По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется соответственно формула:

; .

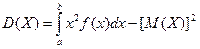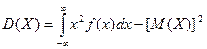Определение. Средним квадратичным отклонениемназывается квадратный корень из дисперсии:

.

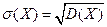Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

.

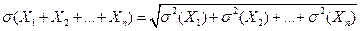Определение. Модой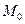дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум:

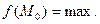
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.

Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным.

Определение. Медианой 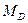случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины:

.

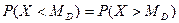Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

Определение. Начальным моментомпорядка k случайной величины Х называется математическое ожидание величины :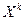

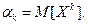
Для дискретной случайной величины: .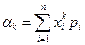

Для непрерывной случайной величины: .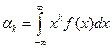

Начальный момент первого порядка равен математическому ожиданию.

Определение.Центральным моментомпорядка k случайной величины Х называется математическое ожидание величины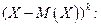

.

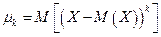Для дискретной случайной величины: .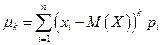

Для непрерывной случайной величины: .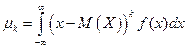

Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.

Определение. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии:

.

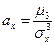Определение.Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом:

.

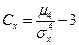Кроме рассмотренных величин используются также так называемые абсолютные моменты.

Абсолютный начальный момент: .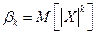

Абсолютный центральный момент: .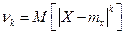

Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.

Пример. Непрерывная случайная величина 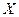задана функцией плотности распределения :

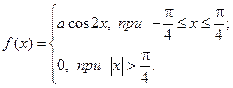
Найти коэффициент 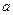, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал 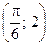. Определить математическое ожидание и дисперсию случайной величины Х.

Для нахождения коэффициента а воспользуемся свойством 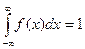. Имеем:

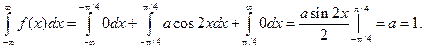
Найдем функцию распределения:

1) На участке :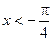

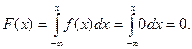
2) На участке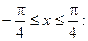

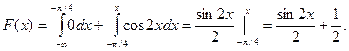
3) На участке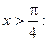

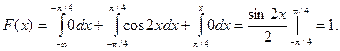
Таким образом: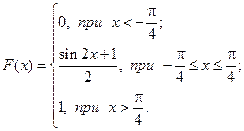

Найдем вероятность попадания случайной величины в интервал .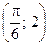

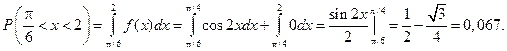
Ту же вероятность можно найти другим способом: