Экстремальные классы для интегральных операторов в равномерной метрике
Критерии оптимальности, рассмотренные выше, не исчерпывают все интересные для приложений ситуации. Важными оказываются критерии, в которых минимизируется верхняя грань абсолютных значений. К таким критериям могут быть сведены требования максимизации функции взаимной корреляции между изучаемым распределением физического параметра и заданным к ней приближением. Минимизация верхней грани соответствует минимизации в равномерной метрике. Это случай нерефлексивных пространств и соответствующая вариационная задача, вообще говоря, не имеет единственного решения. Можно лишь надеяться охарактеризовать свойства одного из решений и, тем самым получить конструктивной описание одной из ветвей экстремального класса 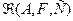 . Сделать это можно лишь в некоторых частных случаях вида оператора
. Сделать это можно лишь в некоторых частных случаях вида оператора  , но они охватывают многие интересные приложения
, но они охватывают многие интересные приложения
Пусть область V есть горизонтальная полоса в нижнем полупространстве 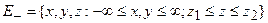 . Пусть, далее, K(x,y,z) – функция из
. Пусть, далее, K(x,y,z) – функция из 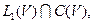 такая что при каждом
такая что при каждом 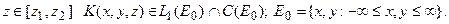 Оператор А определен следующим образом:
Оператор А определен следующим образом:
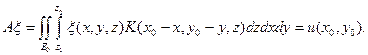 | (5.46) |
Обозначим 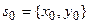 и рассмотрим задачу[23]:
и рассмотрим задачу[23]:
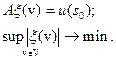 | (5.47) |
В силу свойств функции K(x,y,z) А - непрерывен из 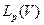 в
в 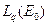 для
для 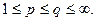 Следовательно, А непрерывен из С(V) в С(Е), и, следовательно,
Следовательно, А непрерывен из С(V) в С(Е), и, следовательно, 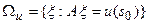 - есть сдвиг замкнутого в C(V) пространства KerA. Тогда решение задачи (47) существует. Однако, в силу того, что норма в C(V) не сильно выпукла, ее решение, вообще говоря, не единственно. Почти тривиален такой результат.
- есть сдвиг замкнутого в C(V) пространства KerA. Тогда решение задачи (47) существует. Однако, в силу того, что норма в C(V) не сильно выпукла, ее решение, вообще говоря, не единственно. Почти тривиален такой результат.
Множество 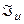 решений задачи (47) при
решений задачи (47) при 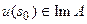
 есть замкнутое выпуклое множество.
есть замкнутое выпуклое множество.
Доказательство. Замкнутость 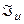 очевидна, поскольку минимизируемый функционал - непрерывен в C(V). Следует доказать выпуклость
очевидна, поскольку минимизируемый функционал - непрерывен в C(V). Следует доказать выпуклость 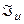 . Пусть
. Пусть 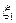 и
и 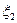 - два решения задачи (47), доставляющие значение d функционалу
- два решения задачи (47), доставляющие значение d функционалу 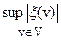 . Тогда их выпуклая комбинация
. Тогда их выпуклая комбинация 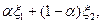
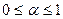 есть также элемент из
есть также элемент из 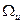 . В силу неравенства:
. В силу неравенства: 
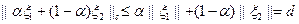 ,
,
имеем 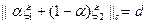 , поскольку в противоположном случае элемент
, поскольку в противоположном случае элемент 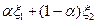 доставлял бы функционалу в (47) меньше, чем d значение и, следовательно,
доставлял бы функционалу в (47) меньше, чем d значение и, следовательно, 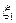 и
и 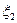 не являлись бы решением задачи (47). Таким образом, любая выпуклая комбинация элементов из
не являлись бы решением задачи (47). Таким образом, любая выпуклая комбинация элементов из 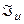 есть снова элемент из
есть снова элемент из 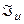 .
.
Существование, но возможная неединственность решения задачи (47), позволяет сделать вывод о том, что экстремальный класс 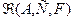 есть полный, но не идеальный, поскольку не есть класс единственности. Поставим перед собой задачу выделения в
есть полный, но не идеальный, поскольку не есть класс единственности. Поставим перед собой задачу выделения в 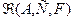 подмножества, являющего почти идеальным, которое будем отождествлять с
подмножества, являющего почти идеальным, которое будем отождествлять с 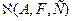 . Прежде чем приступить к дальнейшим рассмотрениям, сделаем следующее замечание. Предположим, что следует решить более общую, чем (47) задачу:
. Прежде чем приступить к дальнейшим рассмотрениям, сделаем следующее замечание. Предположим, что следует решить более общую, чем (47) задачу:
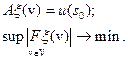 (5.48)
(5.48)
Где 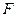 замкнутый оператор, отображающий
замкнутый оператор, отображающий 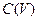 в себя.
в себя.
Тогда замена переменных 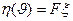 сводит ее к:
сводит ее к:
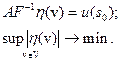 | (5.49) |
Если 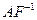 удовлетворяет требованиям, наложенным ранее на оператор А, то, характеризуя элемент
удовлетворяет требованиям, наложенным ранее на оператор А, то, характеризуя элемент 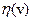 являющийся решением задачи (49), тем самым, будет охарактеризован и элемент
являющийся решением задачи (49), тем самым, будет охарактеризован и элемент 
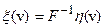 являющийся решением (48) (необходимо, чтобы
являющийся решением (48) (необходимо, чтобы 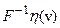 было определено и однозначно).
было определено и однозначно).
В соответствии с теоремой двойственности, для того, чтобы элемент 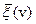 был решением задачи (32), необходимо и достаточно, чтобы в сопряженном к C(V) пространстве
был решением задачи (32), необходимо и достаточно, чтобы в сопряженном к C(V) пространстве 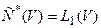 нашелся функционал
нашелся функционал 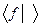 и:
и:
а) 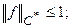
b) 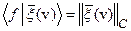 ;
;  (5.50)
(5.50)
c) 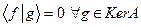 .
.
Схема дальнейших рассуждений следующая. Мы намерены “угадать” вид множества решений задачи (48) при 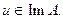 . Далее покажем, что для угаданного элемента могут быть выполнены условия (50а-с), что и будет служить доказательством тому, что “угаданный” элемент действительно служит решением задачи (48). Наконец, покажем, что на выделенном классе из “угаданных” элементов уравнение
. Далее покажем, что для угаданного элемента могут быть выполнены условия (50а-с), что и будет служить доказательством тому, что “угаданный” элемент действительно служит решением задачи (48). Наконец, покажем, что на выделенном классе из “угаданных” элементов уравнение 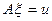 однозначно и плотно разрешимо, что и будет завершать доказательство того, что выделенное множество есть почти идеальный экстремальный подкласс (далее называем его классом) класса
однозначно и плотно разрешимо, что и будет завершать доказательство того, что выделенное множество есть почти идеальный экстремальный подкласс (далее называем его классом) класса 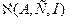 . Дополнительные условия на вид функции
. Дополнительные условия на вид функции 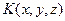 будут вводится по мере надобности, и в конце мы резюмируем результат.
будут вводится по мере надобности, и в конце мы резюмируем результат.
Предположим, что функция 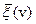 не зависит от вертикальной координаты – z (это и есть “догадка”), т.е.
не зависит от вертикальной координаты – z (это и есть “догадка”), т.е. 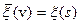 , где s=(x,y).
, где s=(x,y).
В силу теоремы о ядре, устанавливающей ортогональность ядра оператора и множества значений его сопряженного замкнутого в * - слабой топологии (см. прил.2.4) условие (50с) дает выражение для 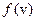 :
: 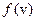 принадлежит * - слабому замыканию
принадлежит * - слабому замыканию 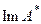 в пространстве
в пространстве 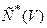 , где:
, где:
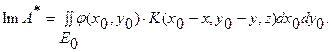 (5.51)
(5.51)
Здесь 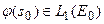 . Это означает, что
. Это означает, что 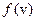 принадлежит множеству пределов последовательностей
принадлежит множеству пределов последовательностей 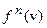 функций из
функций из 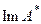 относительно сходимости в смысле:
относительно сходимости в смысле:
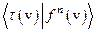 для
для 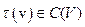 .
.
Пусть 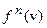 - последовательность элементов из
- последовательность элементов из 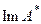 . Тогда:
. Тогда:
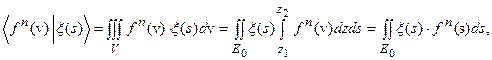
Где 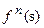 функция, полученная из
функция, полученная из 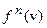 интегрированием по координате
интегрированием по координате 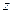 . Эту операцию сокращенно обозначим
. Эту операцию сокращенно обозначим 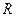 :
:

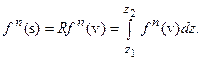
Следует показать, что последовательности 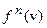 из
из 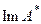 может быть поставлена в соответствие последовательность
может быть поставлена в соответствие последовательность 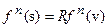 такая, что для ее предельных элементов
такая, что для ее предельных элементов 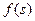 и
и 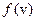 из условия
из условия 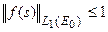 следует
следует 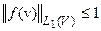 .
.
Если множество функций из С(V), не зависящих от вертикальной координаты и образующих подпространство C(E0) в C(V), не имеет элементов, принадлежащих ядру оператора А, то образ 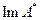 при отображении
при отображении 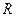 плотен в L1(E0). Действительно, если это не так, то в L1(E0) должен найтись элемент g(s) и
плотен в L1(E0). Действительно, если это не так, то в L1(E0) должен найтись элемент g(s) и
 .
.
Но, отсюда после подстановки выражения 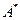 из (51), получим:
из (51), получим:

Последнее означает, что Ag(s)=0, что противоречит условию. В силу доказанной плотности в 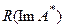 , существует последовательность
, существует последовательность 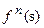 , сходящаяся к
, сходящаяся к 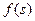 и
и
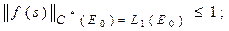
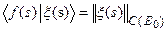 .
.
Далее приведенное выше равенство 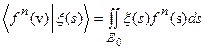 гарантирует выполнение (50b). Следует теперь показать, что и для прообраза
гарантирует выполнение (50b). Следует теперь показать, что и для прообраза 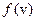 элемента
элемента 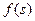 выполнено и условие (50a). Нетрудно видеть, что ||R||=1. Следовательно
выполнено и условие (50a). Нетрудно видеть, что ||R||=1. Следовательно 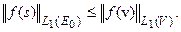 Необходимо доказать строгое равенство. Это будет выполнено в дополнительном предположении:
Необходимо доказать строгое равенство. Это будет выполнено в дополнительном предположении: 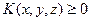 . Действительно, обозначим
. Действительно, обозначим 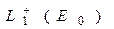 - множество в
- множество в 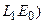 неотрицательных функций, а
неотрицательных функций, а 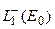 - отрицательных. Ясно, что каждая из функций
- отрицательных. Ясно, что каждая из функций 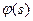 может быть представлена в виде своих положительной
может быть представлена в виде своих положительной 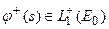 и отрицательной
и отрицательной 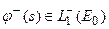 компонент. Тогда:
компонент. Тогда:
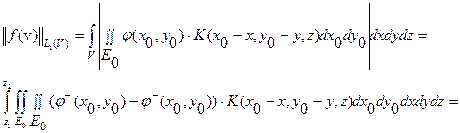
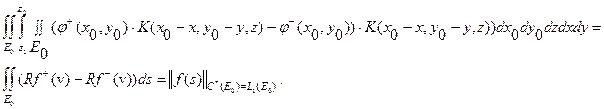
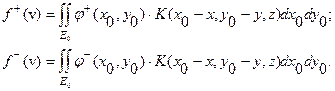
Последнее справедливо в силу положительности функции 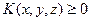 .
.
Требуемое доказано. Предположение о независимости 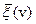 от вертикальной координаты характеризует одно из решений задачи (47).
от вертикальной координаты характеризует одно из решений задачи (47).
Резюмируем сказанное.
Пусть оператор А имеет вид (46), действует из C(V) в C(E0), является линейным, ограниченным и в C(E0) имеет плотную область значений. Если 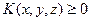 и класс функций из C(V), не зависящих от вертикальной координаты, не входит в ядро операторов А и А*, то множество функций, не зависящих от вертикальной координаты, есть почти идеальный экстремальный класс
и класс функций из C(V), не зависящих от вертикальной координаты, не входит в ядро операторов А и А*, то множество функций, не зависящих от вертикальной координаты, есть почти идеальный экстремальный класс 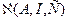 . Напомним, что
. Напомним, что 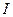 - единичный оператор.
- единичный оператор.
То, что множество независящих от вертикальной координаты функций есть экстремальный подкласс класса 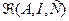 уже выяснено. Условие единственности решения уравнения
уже выяснено. Условие единственности решения уравнения 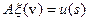 на этом множестве входит в перечень ограничений на оператор
на этом множестве входит в перечень ограничений на оператор  . Следует еще показать, что уравнение
. Следует еще показать, что уравнение 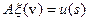 плотно разрешимо на
плотно разрешимо на 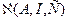 .
.
Если это не так, то в C(E0) существует элемент 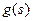 , и
, и
 .
.
Но, тогда:
 ,
,
откуда следует, что 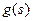 Î KerA*, что противоречит требованиям теоремы о том, что на C(E0) уравнение
Î KerA*, что противоречит требованиям теоремы о том, что на C(E0) уравнение 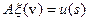 однозначно разрешимо.
однозначно разрешимо.
5.5. Построение решений на экстремальных классах
Идеальные и почти идеальные экстремальныеклассы относительно введенных критериев 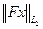 , охватывают большое число случаев. Они включают в себя и рассмотренный ранее случай
, охватывают большое число случаев. Они включают в себя и рассмотренный ранее случай 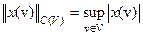 , для операторов представимых в вида (46). Их особая значимость состоит в том, что они образуют линейное подпространство в
, для операторов представимых в вида (46). Их особая значимость состоит в том, что они образуют линейное подпространство в  . Это дает возможность конструктивного решения задачи о выделении элемента на экстремальном классе.
. Это дает возможность конструктивного решения задачи о выделении элемента на экстремальном классе.
Почти идеальный экстремальный класс (41) имеющий представление 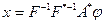 , позволяет с любой наперед заданной точностью решить задачу:
, позволяет с любой наперед заданной точностью решить задачу:
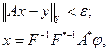
при условии 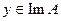 . Для ее решения введем итерационный процесс:
. Для ее решения введем итерационный процесс:
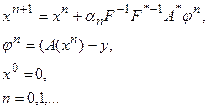 | (5.52) |
Здесь an – параметры релаксации, выбираемые так, чтобы обеспечить сходимость итерационного процесса. В предположении существования параметров релаксации итерационного процесса (52), обеспечивающих его сходимость (позже будет показано, что такой выбор параметров возможен), легко получить:
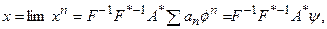 | (5.53) |
где y - некоторый элемент из области определения 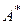 . Таким образом, приходим к выводу о том, что итерационный процесс (52), при условии его сходимости, сходится к решению, имеющему представление (41), являющееся необходимым и достаточным для того, чтобы найденный элемент был решением исходной задачи:
. Таким образом, приходим к выводу о том, что итерационный процесс (52), при условии его сходимости, сходится к решению, имеющему представление (41), являющееся необходимым и достаточным для того, чтобы найденный элемент был решением исходной задачи:
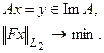
Рассмотрим теперь способ выбора параметра релаксации an, обеспечивающего сходимость итерационного процесса (52).
Потребуемчтобы выбор параметра релаксации обеспечивал максимальную скорость убывания невязки полей 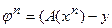 . Легко понять, что:
. Легко понять, что:
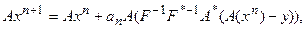 | (5.54) |
Тогда:
jn+1 = Axn+1– y = jn + an A (F-1 F*-1 A* (xn) (A 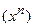 – y)).
– y)).
Выберем в качестве Y гильбертово пространство L2 . Тогда:
||jn+1||2= ||jn||2 + an <jn ½A (F-1 F*-1 A* jn> +an2 || A/ (F-1 F*-1 A* jn||2.
Последнее равенство перепишем в виде: ||jn+1||2= qn ||jn||2, где
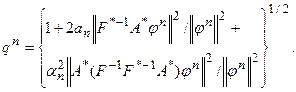 | (5.55) |
В выражении (55) функция qn зависит от an. Максимальная скорость сходимости будет обеспечена, если an минимизирует эту функцию. Для нахождения минимума (экстремума) дифференцируем (55) по an, результат приравниваем к нулю и решаем соответствующее уравнение. В результате получим:
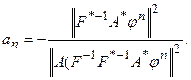 |
В эквивалентной форме:
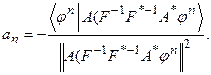 | (5.56) |
Необходимо убедиться, что при выборе параметра релаксации an по формуле (57) значение qn лежит в интервале [0 – 1]. Этим будет обеспечено монотонное убывание невязки 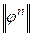 и, тем самым, сходимость итерационного процесса (52) по невязке. Подставив (56) в (55), получим:
и, тем самым, сходимость итерационного процесса (52) по невязке. Подставив (56) в (55), получим:
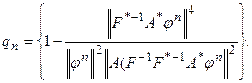 | (5.57) |
Числитель в последнем равенстве перепишем: 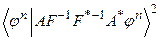 .
.
Отсюда, с учетом хорошо известного неравенства Шварца:
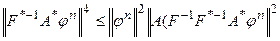 и
и
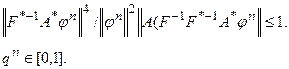
Требуемое доказано – величина qn вещественна, положительна и не превосходит единицы. Этим обеспечивается монотонность убывания невязки и сходимость итерационного процесса.
Рассмотрим предельные случаи. Если при некотором n, 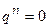 , то это значит, что
, то это значит, что 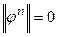 , и процесс сошелся к точному решению A = y. Реально такое положение дел недостижимо. Всегда остается нескомпенсированная невязка. Рассмотрим другой предельный случай -
, и процесс сошелся к точному решению A = y. Реально такое положение дел недостижимо. Всегда остается нескомпенсированная невязка. Рассмотрим другой предельный случай - 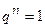 . Из (57) следует, что в этом случае
. Из (57) следует, что в этом случае 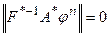 . В силу наложенного ранее условия об отсутствии ненулевого пересечения у ядер операторов F*-1 и A* отсюда вытекает
. В силу наложенного ранее условия об отсутствии ненулевого пересечения у ядер операторов F*-1 и A* отсюда вытекает 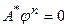 , а в силу известной теоремы о ядре ( см. прил2.4) это означает ортогональность невязки возможному множеству значений оператора
, а в силу известной теоремы о ядре ( см. прил2.4) это означает ортогональность невязки возможному множеству значений оператора 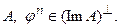 В геофизических терминах этот результат означает то, что достигнутая невязка не может быть компенсирована в рамках введенных модельных представлений, и задача требует введения компонент модели более широких, чем используемые.
В геофизических терминах этот результат означает то, что достигнутая невязка не может быть компенсирована в рамках введенных модельных представлений, и задача требует введения компонент модели более широких, чем используемые.
В реальных ситуациях поле задано с погрешностями, и количество выполняемых итераций необходимо согласовывать с точностью задания поля. На практике итерации продолжаются до тех пор, пока процесс (52) либо не прекратил сходимость, что означает необходимость смены модельных представлений (например, выбор более широкого модельного класса), либо не достигнута требуемая точность: ||jn|| £ d. Условие приостановки итерационного процесса по достижении заданной невязки может быть обобщено и заменено обобщенной невязкой, включающей в себя и оценку погрешности оператора так, как это проделано в 4.3. Однако эти вопросы относятся к числу конкретно-методических для конкретных модификаций методов.
Нелинейные задачи
Касаясь использования критериальных принципов для доопределения решений нелинейных задач, следует выделить два круга вопросов. Во–первых, это собственно характеризация экстремальных классов, которая может быть выполнена в весьма ограничительных предположениях относительно свойств оператора  . Эти ограничения касаются, прежде всего, возможности использования принципов линеаризации задачи – приближенной ее заменой линейным аналогом. Однако после того как линеаризация выполнена, оказываются применимы все методы, изложенные для линейных задач. Во-вторых, это собственно конструктивные приемы построения решений на экстремальных классах. Здесь основой служат итерационные методы, которые применимы и для линейных задач. Однако есть свои особенности, которые касаются, прежде всего, выбора точки, в окрестности которой линеаризация выполняется.
. Эти ограничения касаются, прежде всего, возможности использования принципов линеаризации задачи – приближенной ее заменой линейным аналогом. Однако после того как линеаризация выполнена, оказываются применимы все методы, изложенные для линейных задач. Во-вторых, это собственно конструктивные приемы построения решений на экстремальных классах. Здесь основой служат итерационные методы, которые применимы и для линейных задач. Однако есть свои особенности, которые касаются, прежде всего, выбора точки, в окрестности которой линеаризация выполняется.
5.6.1. Характеристика экстремальных классов для нелинейных задач.
Рассматривая для нелинейного оператора  , отображающего банахово пространство
, отображающего банахово пространство  в банахово пространство
в банахово пространство 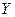 ,постановку, аналогичную (33):
,постановку, аналогичную (33):
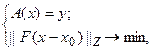 (5.58)
(5.58)
при 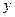 , пробегающим все
, пробегающим все 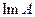 . Предполагая, что F – линейный замкнутый оператор, с ядром, не имеющим общих элементов с
. Предполагая, что F – линейный замкнутый оператор, с ядром, не имеющим общих элементов с 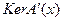 .
. 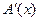 производная Фреше оператора
производная Фреше оператора 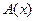 в окрестности решения
в окрестности решения 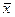 задачи (58), а сам оператор
задачи (58), а сам оператор 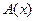 регулярен в окрестности искомого решения, существование которого предполагается, легко получить в случае
регулярен в окрестности искомого решения, существование которого предполагается, легко получить в случае 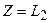 :
:
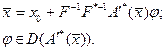 . (5.59)
. (5.59)
Это уравнение по своей форме аналогично уравнению (41), характеризующему почти идеальный экстремальный класс 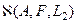 для линейного оператора А. Знак «*» - как и ранее, обозначает перехода к сопряженному оператору. Уравнение (59) легко получается применением принципа Лагранжа (прил.2.6) к задаче (58). Однако оно является лишь необходимым (а не необходимым и достаточным) условием. Кроме того, процесс его получения предполагает непрерывность величины
для линейного оператора А. Знак «*» - как и ранее, обозначает перехода к сопряженному оператору. Уравнение (59) легко получается применением принципа Лагранжа (прил.2.6) к задаче (58). Однако оно является лишь необходимым (а не необходимым и достаточным) условием. Кроме того, процесс его получения предполагает непрерывность величины 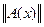 и регулярность оператора А в окрестности
и регулярность оператора А в окрестности 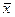 . Но самые большие трудности связаны не с этим. Дело в том, что искомый элемент
. Но самые большие трудности связаны не с этим. Дело в том, что искомый элемент 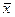 входит не только в левую, но и в правую часть уравнений (59), что затрудняет расчет функции
входит не только в левую, но и в правую часть уравнений (59), что затрудняет расчет функции 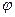 , поскольку она должна быть найдена из уравнения:
, поскольку она должна быть найдена из уравнения:
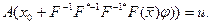 (5.60)
(5.60)
Далеко не всегда ясно, как эти уравнения решать. Для того чтобы избежать всех этих проблем, воспользуемся приемом линеаризации. Однако, несмотря на линеаризацию, решать будем все же нелинейную задачу.
Пусть требуется решить уравнение:
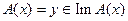 (5.61)
(5.61)
причем заранее неизвестно, имеет ли это уравнение единственное решение либо нет. Пусть задано нулевое приближение к решению - 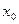 , и оператор А имеет непрерывную производную
, и оператор А имеет непрерывную производную 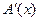 в окрестности
в окрестности 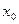 . Если
. Если 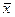 - искомое решение, то для
- искомое решение, то для 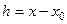 можно записать
можно записать
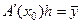 , (5.62)
, (5.62)
где 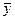 - некоторый элемент, вообще говоря, неизвестный, такой, что для него одно из решений уравнения (62) обладает свойством:
- некоторый элемент, вообще говоря, неизвестный, такой, что для него одно из решений уравнения (62) обладает свойством:
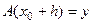 . (5.63)
. (5.63)
Поскольку решение уравнения (62), вообще говоря, неединственно, то следует предположить существование многих правых частей в (62) и соответствующих элементов h таких, что (63) выполнено. Для отбора необходимого h введем, как и ранее, критерий оптимальности в форме функционала:
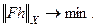 (5.64)
(5.64)
Поскольку оператор 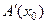 линеен1, то можно к задаче
линеен1, то можно к задаче
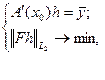 (5.65)
(5.65)
применить результаты п.5.3. В соответствии с ними оператору 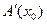 и функционалу
и функционалу 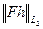 соответствует экстремальный класс
соответствует экстремальный класс 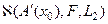 , который при выполнении условий теоремы 2 п.5.2 для оператора F является почти идеальным.
, который при выполнении условий теоремы 2 п.5.2 для оператора F является почти идеальным.
Рассмотрим случай, когда F – линеен, замкнут, имеет ограниченный обратный, и его ядро состоит только из нуля. Тогда почти идеальный экстремальный класс 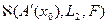 имеет представление
имеет представление
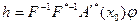 , (5.66)
, (5.66)
Здесь функция 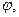 называемая функцией Лагранжа, должна принадлежать области определения оператора
называемая функцией Лагранжа, должна принадлежать области определения оператора 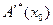 . В достаточных для приложения случаях можно считать, что
. В достаточных для приложения случаях можно считать, что 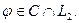
Теперь следует решать задачу:
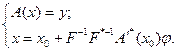 (5.67)
(5.67)
Поскольку ее решение может просто не существовать, перейдем к задаче минимизации
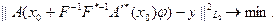
Обобщим ее, введя линейный ограниченный оператор Ф, действующий из ImA в гильбертово пространство Х. Потребуем минимального уклонения преобразования Ф невязки – разности между наблюдаемой u и рассчитанным от искомого решения полем. Тогда получим:
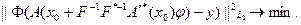 (5.68)
(5.68)
Или:
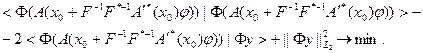
Для нахождения минимума подставим вместо 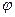 величину
величину 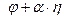 , где
, где  - некоторое число, а
- некоторое число, а 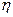 - вариация
- вариация 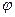 , продифференцируем последнее выражение по
, продифференцируем последнее выражение по  при
при 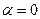 и приравняем результат к нулю:
и приравняем результат к нулю:
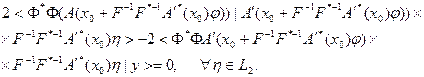
Далее:
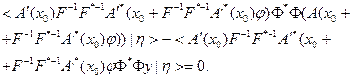
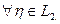
Тогда:
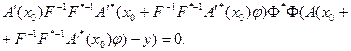 (5.69)
(5.69)
Класс 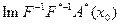 является почти идеальным для уравнения
является почти идеальным для уравнения
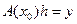 . (5.70)
. (5.70)
Это означает, что уравнение (60) однозначно решаемо на множестве 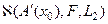 . Предположим, что уравнение (60) однозначно разрешимо и на множестве
. Предположим, что уравнение (60) однозначно разрешимо и на множестве

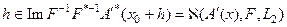 ,
,
что будет, например, выполнено при:
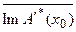 =
= 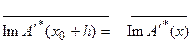 . (5.71)
. (5.71)
Тогда из (69) следует:
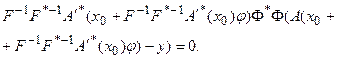
Далее, учитывая, что для искомого решения  :
:
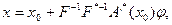
имеем
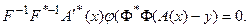 (5.72)
(5.72)
