Анализ полученных решений
Формулы (4.70)…(4.72) однотипны и могут быть описаны одним уравнением
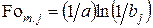 . (4.76)
. (4.76)
При 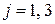 имеем расчет напряжений на поверхности и в центре, а при
имеем расчет напряжений на поверхности и в центре, а при 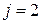 — перепада температур. После определения максимальных времен можно найти соответствующие температуры при этих числах Фурье с учетом двух членов ряда.
— перепада температур. После определения максимальных времен можно найти соответствующие температуры при этих числах Фурье с учетом двух членов ряда.
Подставляя 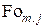 в уравнение (4.60), получим температуру поверхности
в уравнение (4.60), получим температуру поверхности
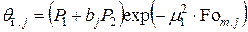 , (4.77)
, (4.77)
в (4.61) — температуру центра
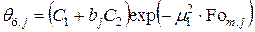 , (4.78)
, (4.78)
в соотношение (4.62) — среднемассовую
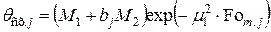 , (4.79)
, (4.79)
и в (4.65) перепад температур
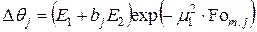 . (4.80)
. (4.80)
Наибольшую и основную трудность при практических расчётах по уравнениям (4.56)…(4.80) представляет определение по соотношению (4.69) бесчисленного множества корней. В работе [3] приведена общая приближенная формула расчета первого корня для тел простой формы
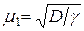 , (4.81)
, (4.81)
где 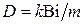 ;
; 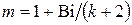 -коэффициент термической массивности;
-коэффициент термической массивности;
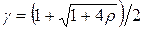 ;
; 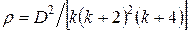 ;
; 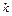 — коэффициент геометрической формы, равный 1 – для пластины, 2 – цилиндра и 3 – шара. При малых r число
— коэффициент геометрической формы, равный 1 – для пластины, 2 – цилиндра и 3 – шара. При малых r число 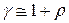 .
.
Для определения приближенных значений остальных корней следует различать два характерных случая нагрева – при больших и малых числах Био [14].
При малых числах Био (Bi < 3)
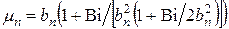 , (4.82)
, (4.82)
где 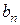 — корни уравнения (14) при
— корни уравнения (14) при 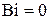 , т.е. нули функции
, т.е. нули функции 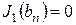 :
: 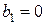 ;
; 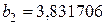 ;
; 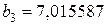 и т.д. [14].
и т.д. [14].
При больших числах Био ( 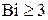 )
)
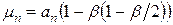 , (4.83)
, (4.83)
где 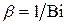 ;
;
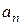 — корни уравнения (4.69) при
— корни уравнения (4.69) при 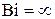 , т.е. нули функции
, т.е. нули функции 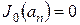 :
:
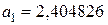 ;
; 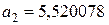 и т.д.
и т.д.
Следует отметить, что при числах Био 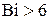 первый корень
первый корень 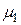 следует вычислять не по уравнению (4.81), а по (4.83).
следует вычислять не по уравнению (4.81), а по (4.83).
Получим упрощенные расчетные соотношения в двух предельных случаях.
4.2.1. Асимптотика при малых числах Био.
Первый корень уравнения (4.69) вычисляем по соотношению (4.81) при 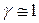 и
и 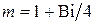 , а второй — по (4.82). Тогда отношение собственных чисел
, а второй — по (4.82). Тогда отношение собственных чисел
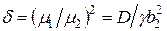 . (4.84)
. (4.84)
Разность квадратов корней 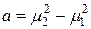
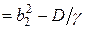 .
.
Первая амплитуда, входящая в уравнение (4.60) температуры поверхности
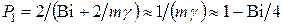 . (4.85)
. (4.85)
По аналогии вторая 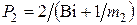 и любая
и любая
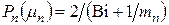 , (4.86)
, (4.86)
где 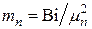 — n-ый коэффициент термической массивности.
— n-ый коэффициент термической массивности.
Интересно отметить, что в отличие от других амплитуд зависимость 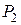 от числа Био носит немонотонный характер, возрастает от нуля до максимального значения
от числа Био носит немонотонный характер, возрастает от нуля до максимального значения 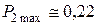 при числе
при числе 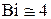 , а затем уменьшается до нуля, оставаясь меньше
, а затем уменьшается до нуля, оставаясь меньше 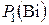 .
.
Введем отношение поверхностных амплитуд
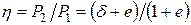 , (4.87)
, (4.87)
где 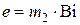 .
.
При определении тепловой амплитуды 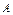 воспользуемся разложением функции Бесселя при малых аргументах
воспользуемся разложением функции Бесселя при малых аргументах 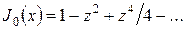 , где
, где 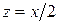 . Тогда
. Тогда
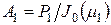
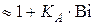 , (4.88)
, (4.88)
где 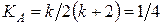 .
.
Согласно [126] вторая амплитуда
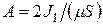 , (4.89)
, (4.89)
где 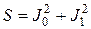 ; при больших аргументах
; при больших аргументах 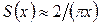 .
.
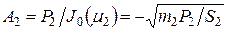 , (4.90)
, (4.90)
где 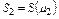 .
.
Для среднемассовой температуры:
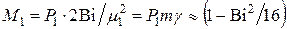 и
и 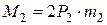 . (4.91)
. (4.91)
Для перепада температур по уравнению (4.65)
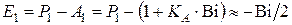 , (4.92)
, (4.92)
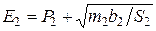 .
.
Для термических напряжений в центре цилиндра по (4.58)
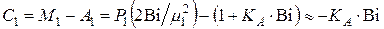 . (4.93)
. (4.93)
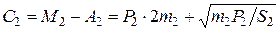 .
.
Для термонапряжений на поверхности
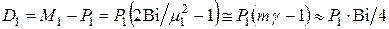 , (4.94)
, (4.94)
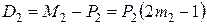 .
.
С целью проверки амплитуды 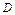 можно использовать равенство
можно использовать равенство 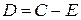 .
.
Выражения для расчета максимальных времен по уравнению (4.76) также упростятся.
Коэффициент поверхности 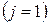
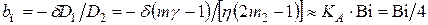 ,
,
для перепада температур 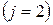
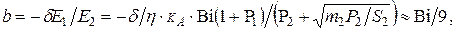 (4.95)
(4.95)
и центра 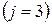
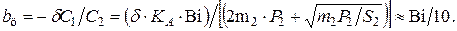
Результаты расчетов при 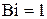 максимальных времен
максимальных времен 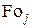 по формуле (4.76) и соответствующих этим временам максимальных термических напряжений на поверхности по уравнению (4.74),
по формуле (4.76) и соответствующих этим временам максимальных термических напряжений на поверхности по уравнению (4.74), 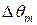 по (4.73) и термонапряжений в центре цилиндра по (4.75) приведены в табл. 4.1. Там же представлены данные при
по (4.73) и термонапряжений в центре цилиндра по (4.75) приведены в табл. 4.1. Там же представлены данные при 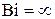 .
.
Таблица 4.1. Коэффициенты 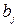 , максимальные времена
, максимальные времена 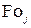 ,
, 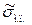 ,
, 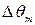 и
и 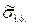 при
при 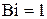 и
и 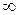 .
.
| j | Число Био 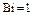 | 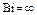 | |||||
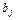 | 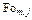 | 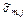 | 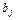 | 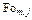 | 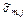 | ||
| 0,197687 | 0,107603 | 0,159055 | |||||
| 0,101219 | 0,152036 | –0,306981 | 0,28556 | 0,05074 | –0,96792 | ||
| 0,069518 | 0,176974 | –0,152570 | 0,14446 | 0,07837 | –0,46734 | ||
Анализ уравнений (4.76) и (4.95) позволяет сделать вывод о том, что максимум величин наступает в последовательности 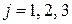 и с ростом числа Био эти времена уменьшаются.
и с ростом числа Био эти времена уменьшаются.
Для оценки различия максимальных времен при 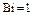 составим их разности:
составим их разности:
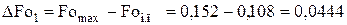 ;
;
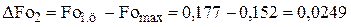
и 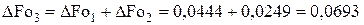 . (4.96)
. (4.96)
Из (4.76) и табл. 1 следует, что с ростом числа Био различия максимальных времен увеличиваются, вплоть до 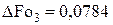 – см. уравнение (4.105).
– см. уравнение (4.105).
На практике технологов интересует вопрос — насколько термические напряжения на поверхности тела больше, чем в его середине. Обозначим их отношение 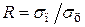 . Наиболее просто
. Наиболее просто 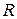 можно найти в стадии регулярного режима нагрева (РРН), который наступает при числах Фурье
можно найти в стадии регулярного режима нагрева (РРН), который наступает при числах Фурье 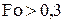 и когда вместо бесконечных сумм в уравнениях (4.57)…(4.65) можно ограничиться одним членом ряда. Тогда, деля уравнение (4.57) на (4.58) и учитывая упрощенные соотношения (4.93) и (4.94), получим
и когда вместо бесконечных сумм в уравнениях (4.57)…(4.65) можно ограничиться одним членом ряда. Тогда, деля уравнение (4.57) на (4.58) и учитывая упрощенные соотношения (4.93) и (4.94), получим
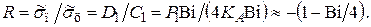 (4.97)
(4.97)
При числе 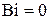
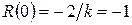 .
.
Таким образом, в отличие от процесса нагрева плоских тел, когда при 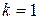
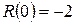 , термические напряжения на поверхности тела в 2 раза больше термонапряжений в центре, при нагреве цилиндрических тел напряжения в центральных точках тела примерно равны или чуть больше, чем на поверхности.
, термические напряжения на поверхности тела в 2 раза больше термонапряжений в центре, при нагреве цилиндрических тел напряжения в центральных точках тела примерно равны или чуть больше, чем на поверхности.
4.2.2. Асимптотика при больших числах Био.
Теперь корни 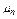 , в том числе и первый, находим по уравнению (4.83). Тогда отношение
, в том числе и первый, находим по уравнению (4.83). Тогда отношение
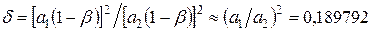 . (4.98)
. (4.98)
В данном случае отношение корней совпадает с максимально возможным, которое получается в предельном случае при 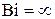 :
: 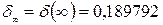 .
.
Разность квадратов корней
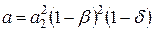 . (4.99)
. (4.99)
Амплитуды:
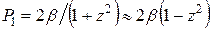 ;
;
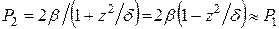 ,
,
где 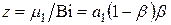 .
.
В работе [13] было получено, что тепловая амплитуда при больших числах Био для плоских тел пропорциональна 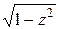 . Предполагая такую же зависимость для любых тел, получим
. Предполагая такую же зависимость для любых тел, получим
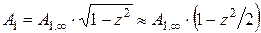 ; (4.100)
; (4.100)
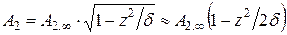 ,
,
где 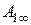 и
и 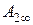 — амплитуды при
— амплитуды при 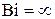 . Осуществляя в уравнении (4.89) предельный переход при
. Осуществляя в уравнении (4.89) предельный переход при 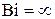 , т.е. полагая в нем
, т.е. полагая в нем 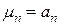 и
и 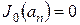 , будем иметь
, будем иметь
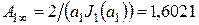 ;
; 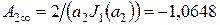 .
.
Расчет амплитуды по уравнению (4.100) при 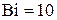 дает
дает 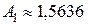 с погрешностью 0,3% по сравнению с точным значением
с погрешностью 0,3% по сравнению с точным значением 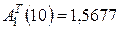 [126].
[126].
Амплитуды:
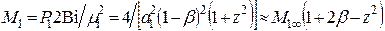 ;
; 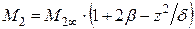 ,
,
где 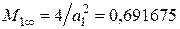 ;
; 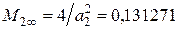 .
.
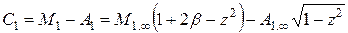 ;
;  ;
; 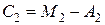 ;
; 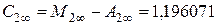 .
.
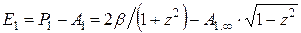 ;
; 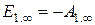 ;
; 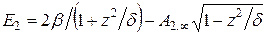 ;
; 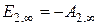 .
.
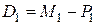 ;
; 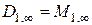 ;
; 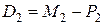 ;
; 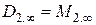 .
.
Теперь коэффициенты для расчета максимальных времен примут вид:
 ; (4.101)
; (4.101)
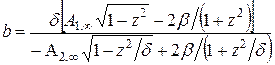 ; (4.102)
; (4.102)
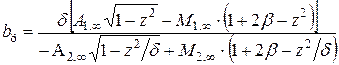 . (4.103)
. (4.103)
В предельном случае при 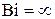 :
:
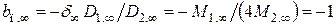 ;
; 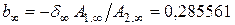 ;
;
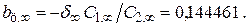 (4.104)
(4.104)
Так как 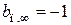 лишено физического смысла, следует взять
лишено физического смысла, следует взять 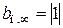 .
.
Тогда наименьшие максимальные времена согласно (4.76) при 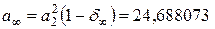 будут:
будут:
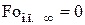 ,
, 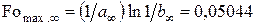
и 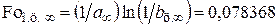 . (4.105)
. (4.105)
Подставляя (4.105) в уравнение (4.58), получим максимально возможное термическое напряжение в центре цилиндра
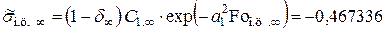 . (4.106)
. (4.106)
Величины 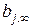 , вычисленные по уравнению (4.104), времена
, вычисленные по уравнению (4.104), времена 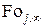 согласно (4.105) и максимальные термические напряжения
согласно (4.105) и максимальные термические напряжения 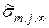 приведены в табл.4.1.
приведены в табл.4.1.
Отношение термонапряжений при 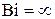
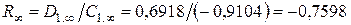 .
.
Следует отметить, что если приближенно считать 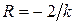 , то из уравнения (4.64) будем иметь
, то из уравнения (4.64) будем иметь
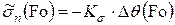 , (4.107)
, (4.107)
где 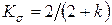 .
.
Это соотношение при 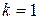 и 2 полностью совпадает с формулами Н.Ю. Тайца [28] для максимальных термических напряжений
и 2 полностью совпадает с формулами Н.Ю. Тайца [28] для максимальных термических напряжений
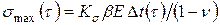 . (4.108)
. (4.108)
Из анализа уравнения (46) вытекает, что коэффициент 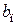 меняет знак по причине изменения знака амплитуды
меняет знак по причине изменения знака амплитуды 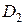 , изменяющейся от
, изменяющейся от 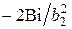 при малых числах Био до
при малых числах Био до 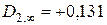 . Из условия равенства нулю
. Из условия равенства нулю 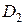 можно получить граничное число
можно получить граничное число 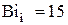 выше которого имеем случаи нагрева термически «массивного» тела. Таким образом, при числах
выше которого имеем случаи нагрева термически «массивного» тела. Таким образом, при числах 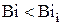 для определения времени
для определения времени 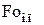 можно применять формулу (4.70) в которой
можно применять формулу (4.70) в которой 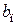 определяется по уравнению (4.101), а при
определяется по уравнению (4.101), а при 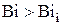 коэффициент
коэффициент 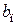 становится отрицательным и нельзя пользоваться формулой (4.70). Возникшую ситуацию можно объяснить следующим образом. Формулы (4.70)…(4.76) получены с учетом всего двух членов ряда. С ростом числа Био максимальное время
становится отрицательным и нельзя пользоваться формулой (4.70). Возникшую ситуацию можно объяснить следующим образом. Формулы (4.70)…(4.76) получены с учетом всего двух членов ряда. С ростом числа Био максимальное время 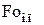 уменьшается, вплоть до 0 при
уменьшается, вплоть до 0 при 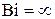 .
.
При очень малых числах Фурье 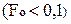 расчёт температур по уравнениям (4.56)…(4.65) затруднителен из-за необходимости учета большого количества членов ряда, ввиду его плохой сходимости. В этом случае для расчёта поверхностной температуры можно использовать формулы, полученные методом операционного исчисления в работе [126]. Объединяя эти формулы в одно уравнение для простых тел, будем иметь:
расчёт температур по уравнениям (4.56)…(4.65) затруднителен из-за необходимости учета большого количества членов ряда, ввиду его плохой сходимости. В этом случае для расчёта поверхностной температуры можно использовать формулы, полученные методом операционного исчисления в работе [126]. Объединяя эти формулы в одно уравнение для простых тел, будем иметь:
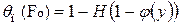 , (4.109)
, (4.109)
где 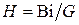 ;
; 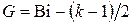 ;
;
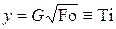 – модифицированное время, число Тихонова;
– модифицированное время, число Тихонова;
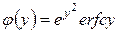 ;
; 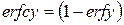 — дополнительный интеграл вероятностей;
— дополнительный интеграл вероятностей;
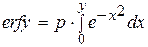 — функция ошибок Гаусса;
— функция ошибок Гаусса; 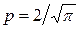 ;
;
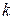 — фактор формы, см. уравнение (4.81).
— фактор формы, см. уравнение (4.81).
Зная температуру поверхности и используя методику [13], можно найти среднемассовую температуру
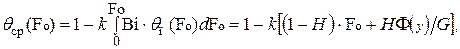 (4.110)
(4.110)
где 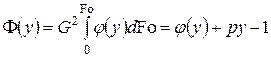 .
.
При числах 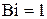 для шара или
для шара или 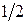 для цилиндра коэффициент
для цилиндра коэффициент 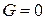 и в расчетных соотношениях (4.109) и (4.110) следует раскрывать неопределенность типа
и в расчетных соотношениях (4.109) и (4.110) следует раскрывать неопределенность типа 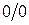 . Используя разложение функции
. Используя разложение функции 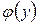 при малых аргументах, из уравнения (4.109) получим для температуры на поверхности:
при малых аргументах, из уравнения (4.109) получим для температуры на поверхности:
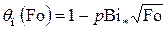 (4.111)
(4.111)
и для среднемассовой из (4.110)
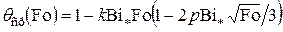 , (4.112)
, (4.112)
где 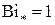 и
и 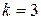 для шара и
для шара и 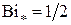 и
и 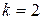 — для длинного цилиндра.
— для длинного цилиндра.
Таким образом, при малых временах процесса ( 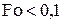 ) вместо уравнения (4.60) будет (4.109), вместо (4.62)…(4.110), а температуру в центре тела на начальной стадии нагрева приближенно можно принять
) вместо уравнения (4.60) будет (4.109), вместо (4.62)…(4.110), а температуру в центре тела на начальной стадии нагрева приближенно можно принять 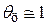 .
.
С учетом сказанного уравнение (4.57) для расчета термических напряжений на поверхности примет вид
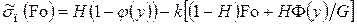 . (4.113)
. (4.113)
При 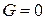 , после раскрытия неопределенности с помощью (56), получим
, после раскрытия неопределенности с помощью (56), получим
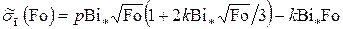 . (4.114)
. (4.114)
Дифференцируя уравнение (4.113) по времени и приравнивая производную нулю с учетом разложений можно получить формулу, анало-гично (4.70), для расчета времени наступления 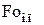 максимального термического напряжения на поверхности. Ввиду сложности (4.113) и необходимости в дальнейшем решать трансцендентные уравнения, покажем ход расчета на более простом уравнении (4.114). Из соотношения
максимального термического напряжения на поверхности. Ввиду сложности (4.113) и необходимости в дальнейшем решать трансцендентные уравнения, покажем ход расчета на более простом уравнении (4.114). Из соотношения 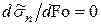 получим квадратное уравнение, решение которого имеет вид:
получим квадратное уравнение, решение которого имеет вид:
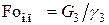 , (4.115)
, (4.115)
где 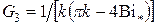 ;
; 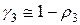 ;
; 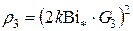 .
.
Расчет для цилиндра при 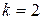 и
и 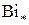 =1/2 дает
=1/2 дает 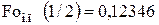 , что хорошо согласуется с ранее полученной при
, что хорошо согласуется с ранее полученной при 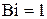 по (4.70) величиной 0,1076 (см. табл. 4.1).
по (4.70) величиной 0,1076 (см. табл. 4.1).
Иногда требуется определить расположение координаты 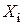 нейтрального слоя в котором термические напряжения меняют знак с
нейтрального слоя в котором термические напряжения меняют знак с 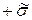 на
на 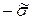 , т.е. в этой точке равны нулю. Наиболее просто это можно сделать в стадии РРН. Тогда согласно уравнению (1)
, т.е. в этой точке равны нулю. Наиболее просто это можно сделать в стадии РРН. Тогда согласно уравнению (1) 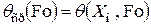 или
или 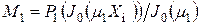 . Разрешая последнее выражение относительно
. Разрешая последнее выражение относительно 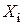 , с помощью разложения функции
, с помощью разложения функции 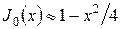 — см. уравнение (4.88), получим при малых числах Био
— см. уравнение (4.88), получим при малых числах Био
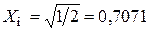 . (4.116)
. (4.116)
и при больших числах Био
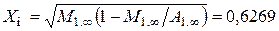 . (4.117)
. (4.117)
Таким образом, поскольку 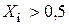 нейтральные слои расположены ближе к поверхности, а само
нейтральные слои расположены ближе к поверхности, а само 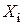 колеблется в узких пределах — от 0,63 до 0,71.
колеблется в узких пределах — от 0,63 до 0,71.
Следует отметить, что при нагреве абсолютные, т.е. размерные термические напряжения 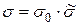 поменяют знаки за счет отрицательности
поменяют знаки за счет отрицательности 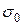 из-за
из-за 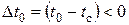 .
.
В заключение укажем, что все полученные решения описывают как процесс конвективного нагрева цилиндрических тел, так и их охлаждение.
