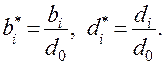Выберем теперь характеристический полином замкнутой системы в виде

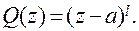
Выберем минимальный порядок системы l = l_min = 2 и выберем произвольно а = 0.6. Составив и решив систему алгебраических уравнений, получим

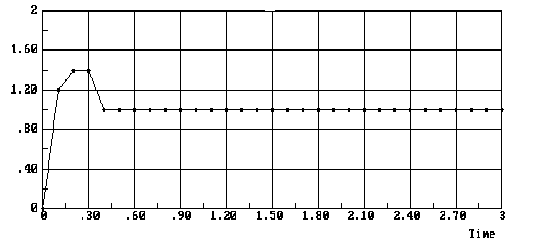
Рис.8.10.Переходный процесс конечной, но неминимальной длительности

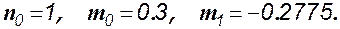
Вычислив передаточную функцию, получим переходный процесс (рис.8.11).

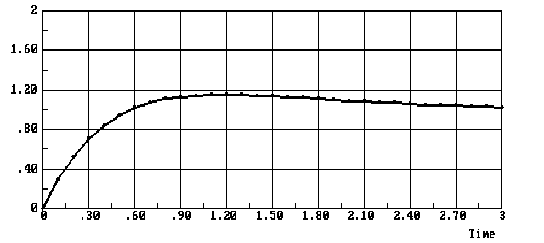
Рис.8.11.Переходный процесс неминимальной и неконечной длительности
Показатели качества такой системы (s=16%, t_p=2.7c) вполне приемлемы.

8.7. Операционные методы цифрового моделирования дискретно – непрерывных систем.

Для исследования дискретно – непрерывных САУ широко рапространено моделирование их динамики на ЦВМ. Математическая модель для ее программирования на ЦВМ в любом случае сводится к описанию системы в форме разностных уравнений. Разностное уравнение (уравнение в конечных разностях) является аналогом дифференциальных уравнений в дискретной области. Формально переход от дифференциального уравнения к разностному осуществляется путем замены в первом производных конечными разностями в соответсивии с выражением

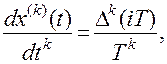(8.44)

где 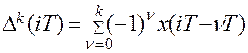- конечная разность к – го порядка. Пусть дифференциальное уравнение системы имеет вид

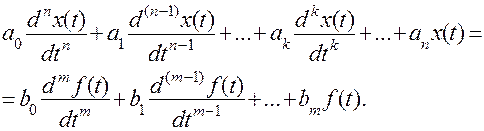
Подставив иместо производных выражения вида (8.44) и учитывая формулу конечных разностей, после преобразований получим

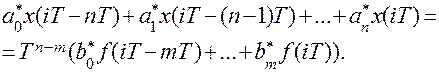(8.45)

Это и есть уравнение системы в конечных разностях. В этом уравнении 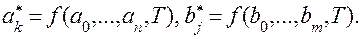Разностное уравнение дает возможность получить рекуррентную формулу для вычисления для вычисления

i – го значения выходной величины по ее прошлым значениям и значениям входной величины

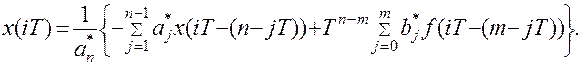(8.46)

Рекуррентное выражение легко программируется для вычислений на ЦВМ.

Недостатком такой математической модели является то, что начальное значение выходной величины не равно нулю: 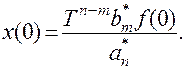При малых значениях периода дискретизации эта ошибка невелика и ею можно пренебречь. С увеличением числа тактов вычислений ошибка дискретной модели непрерывной системы быстро уменьшается. Начальную ошибку можно исключить ее вычитанием из правой части (8.46) при i=0 .

Применив Z – преобразование к (8.45) и учитывая теорему запаздывания, поучим передаточную Z – функцию непрерывной системы

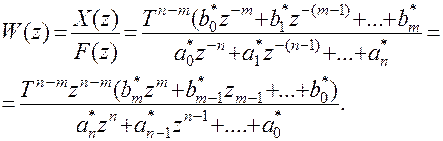(8.47)

Отсюда следует, что, зная передаточную функцию дискретной системы в аппарате Z – изображений, легко получить моделирующее ее разностное уравнение.

Важным обстоятельством является то, что при иммитационном моделировании операцию преобразования дифференциального уравнения в разностное можно применить отдельно к каждому элементу непрерывной части системы и попученные уравнения включить в общую систему разностных уравнений,моделирующую дискретно – непрерывную САУ.

Пример. Передаточная функция элемента непрерывной части системы имеет вид

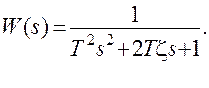
Требуется получить соответствующее разностное уравнение. При Т=0.5 иz =0.3 переходная функция непрерывного элемента имеет вид, показанный на ис.8.12.

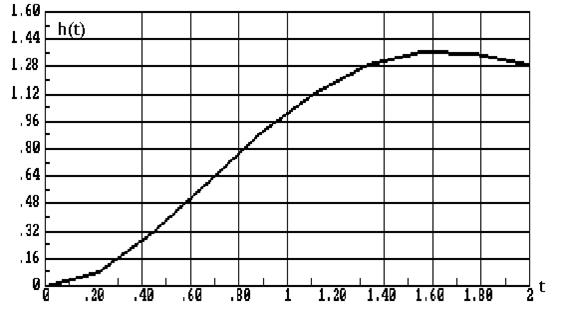
Рис.8.12. Переходная функция непрерывного элемента

При заданных значениях параметров путем описанных выше преобразований получим разностное уравнение для Т=0.1

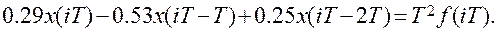
Отсюда для рекуррентного выражения можно записать

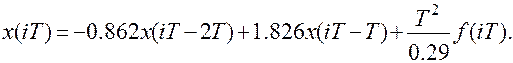
Производя вычисления по полученной рекуррентной формуле с учетом вычитания начальной ошибки при i=0, получим для f(t)=1(t) переходную функцию, показанную на рис.8.13. Сопоставляя ординаты процессов, приведенных на рис.8.12 и 8.13 в точкахквантования по времени, легко убедиться, что уже после пятого шага вычисле ний отличие дискретного процесса от точного не превышает 5%. Совершенно аналогичный результат получим, если для построения переходного процесса использовать передаточную функцию вида (8.47), предварительно умноженную на z ^–1 для обеспечения выполнения условия x(0)=0.

Допустим, что каким – либо способом получена передаточная функция вычислительной машины и требуется получить для программирования соответствующее разностное уравнение.

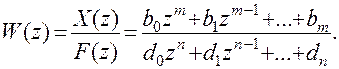(8.48)

Разделим числитель и знаменатель в (8.48) на 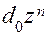. Получим

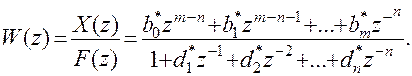
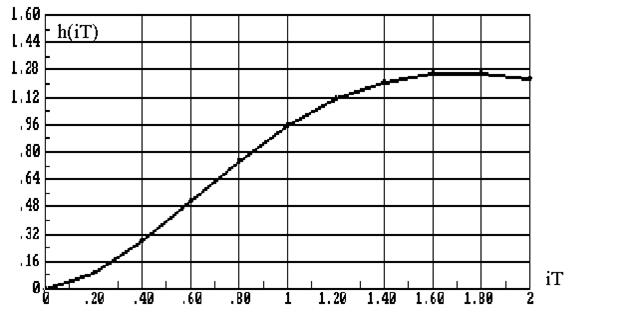
Рис.8.13. Переходная функция непрерывного элемента, вычисленная

по разностному уравнению

В этом выражении