Динамика движения вещества
Рассмотрим эволюционную задачу в (4), считая, что управляющие динамические параметры[25] 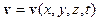 и
и 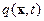 заданы:
заданы:
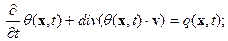 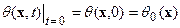 . . | (6.7) |
Разобьем весь временной промежуток 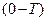 на достаточно малые интервалы времени
на достаточно малые интервалы времени 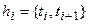
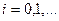 , в пределах каждого из которых можно считать
, в пределах каждого из которых можно считать 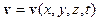 и
и 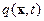 стационарными. Обозначим
стационарными. Обозначим 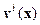 и
и 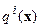 их значения на соответствующих временных интервалах
их значения на соответствующих временных интервалах 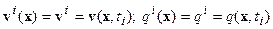 . Для каждого из интервалов выпишем задачу (7):
. Для каждого из интервалов выпишем задачу (7):
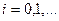 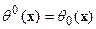 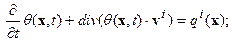 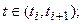 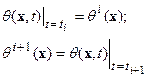 | (6.7) |
Строгое решение задачи (7) достаточно трудоемко [1,2] и требует введения специальных математических понятий, выходящих за рамки обычного курса для ВУЗов. В этой связи приведем упрощенные, символьные рассмотрения, которые иллюстрируют суть методов вполне достаточно, чтобы служить основой для конструктивных результатов. Приводимое ниже следует рассматривать как пояснения, но не как вывод и доказательство.
Обозначим 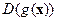 оператор:
оператор: 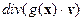 , отображающий функцию
, отображающий функцию 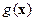 в
в 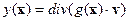 . Обозначим символом
. Обозначим символом 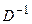 обратный к
обратный к 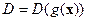 так, что
так, что 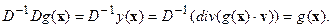 Этот оператор многозначен, поскольку однородное уравнение
Этот оператор многозначен, поскольку однородное уравнение 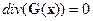 имеет нетривиальное решение в виде
имеет нетривиальное решение в виде 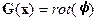 , где
, где 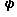 - векторный потенциал. В этой связи можно записать
- векторный потенциал. В этой связи можно записать 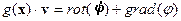 , где
, где 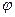 - скалярный потенциал. Вводя условие калибровки
- скалярный потенциал. Вводя условие калибровки 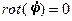 , получаем
, получаем 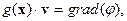 откуда, для определения скалярного потенциала получаем уравнение Пуассона:
откуда, для определения скалярного потенциала получаем уравнение Пуассона: 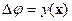 . Частным решением этой задачи задается интегралом Пуассона:
. Частным решением этой задачи задается интегралом Пуассона:
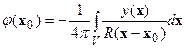 .
.
Здесь 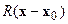 - евклидово расстояние между точками
- евклидово расстояние между точками 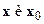 . Во всех этих рассмотрениях важно на самом деле лишь то, что оператор
. Во всех этих рассмотрениях важно на самом деле лишь то, что оператор 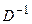 может быть определен.
может быть определен.
Вернемся к уравнению (7), записав его в форме
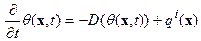 . В силу очевидного равенства: . В силу очевидного равенства: 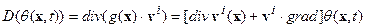 , Перепишем его в эквивалентном виде: , Перепишем его в эквивалентном виде: 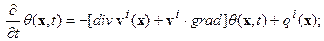 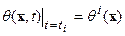 | (6.8) |
Если 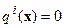 , то решение задачи:
, то решение задачи:
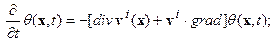 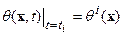 , , | (6.9) |
можно представить в виде операторного соотношения:
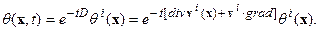 | (6.10) |
Его справедливость проверяется простым дифференцированием:
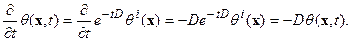
Если 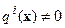 , то (8) сводится к (9) при условии, что
, то (8) сводится к (9) при условии, что 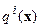 и, как следствие,
и, как следствие, 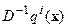 не содержит времени
не содержит времени 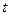 :
:
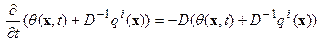 .
.
Считая, что 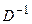 ,
, 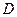 и
и 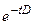 коммутируют (что на самом деле имеет место), получаем, из (9):
коммутируют (что на самом деле имеет место), получаем, из (9):
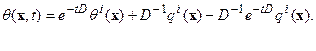 В более подробной записи: В более подробной записи: 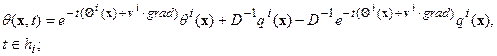 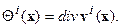 Следовательно: Следовательно: 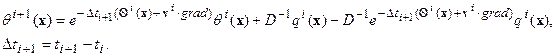 | (6.11) |
Экспонента от операторапонимается в следующем смысле: если X линейный, замкнутый оператор, куда, в частности относятся операторы дифференцирования, умножения на весовые функции и все ограниченные операторы, то
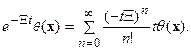
Подставим вместо 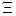 оператора дифференцирования -
оператора дифференцирования - 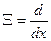 . Тогда:
. Тогда:
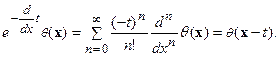
Отсюда нетрудно получить, в частности:
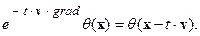 | (6.12) |
Последнее соотношение позволит дать алгоритмическую интерпретацию для (11). Она состоит в том, что одним из действий, входящим в (11), а именно действие 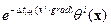 , следует понимать как сдвиг
, следует понимать как сдвиг 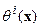 в направлении
в направлении 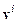 на величину
на величину 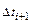 . Однако (11) можно еще более упростить, заменив его приближенным аналогом.
. Однако (11) можно еще более упростить, заменив его приближенным аналогом.
Соотношение (10) дает решение для задачи (9):
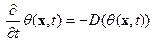 ;
;
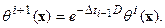
Эти два соотношения определяют трансформацию « на +1 шаг» предшествующего положения для распределения 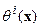 . В конечных разностях в первом случае имеем:
. В конечных разностях в первом случае имеем:
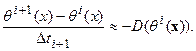
Во втором:
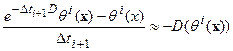
Тогда:
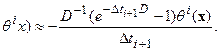
Считая, что эти уравнения справедливы для компенсационных источников 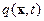 , получим:
, получим:
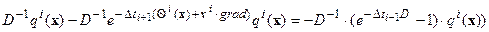 .
.
Тогда:
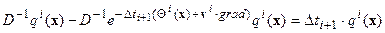 .
.
Таким образом, соотношение (11) приближенно переписывается так:
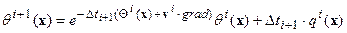 | (6.13) |
Вычислительную схему (13), а именно, введение в итерационный процесс свободного компенсационного члена, можно получить иначе.
Если в (7) положить 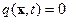 , то описание эволюции подчиняется уравнению (10). Ввести дополнительный член
, то описание эволюции подчиняется уравнению (10). Ввести дополнительный член 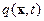 , и тем самым, свести (10) к (13) можно именно на этом этапе, интерпретируя его как компенсационный член, добавляемый пошагово для обеспечения баланса «количества вещества». На следующем шаге этот член
, и тем самым, свести (10) к (13) можно именно на этом этапе, интерпретируя его как компенсационный член, добавляемый пошагово для обеспечения баланса «количества вещества». На следующем шаге этот член 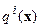 участвует в «эволюции» системы как равноправная компонента вещества, а его приток, если он есть, учитывается новой порцией
участвует в «эволюции» системы как равноправная компонента вещества, а его приток, если он есть, учитывается новой порцией 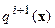 .
.
Принимая во внимание (12) можно дать следующую интерпретацию для (13). Эволюция модели распределения параметра 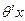 на каждом из интервалов
на каждом из интервалов 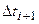 складывается из комбинации деформационной
складывается из комбинации деформационной 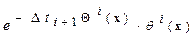 , сдвиговой
, сдвиговой 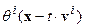 и дивергентной
и дивергентной 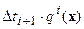 компонент. На следующем шаге вновь полученная модель эволюционирует с новыми параметрами. В частности, осуществляется перенос и дивергентной компоненты по законам для всего распределения.
компонент. На следующем шаге вновь полученная модель эволюционирует с новыми параметрами. В частности, осуществляется перенос и дивергентной компоненты по законам для всего распределения.
Поскольку операторы grad и умножения на весовую функцию Θ(x) не коммутируют, в уточнении нуждается смысл выражения:
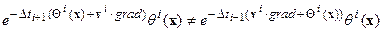 .
.
В общем случае
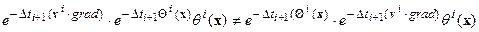 .
.
Смысл этого обстоятельства состоит в том, что сдвиг и последующее сжатие, вообще говоря, не дают тот же результат, что сжатие и последующий сдвиг[26].
В значительном числе случаев этим различием можно пренебречь, что выполняется, в частности, при плавном изменении величины Θ, либо условии несжимаемости среды ‑ 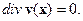 Однако, даже если эти условия не выполняются, с точки зрения алгоритма моделирования процесса эволюции, при условии уточнения в процессе моделирования геодинамических параметров, оба эти подхода практически совпадают.
Однако, даже если эти условия не выполняются, с точки зрения алгоритма моделирования процесса эволюции, при условии уточнения в процессе моделирования геодинамических параметров, оба эти подхода практически совпадают.
С учетом высказанного замечания уравнение движения (13) содержит две компоненты – сдвигово-деформационную:
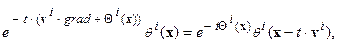
регулируемую векторной скоростью 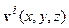 , определяющей величину, направление перемещения и деформации параметра в процессе эволюции, и дивергентную
, определяющей величину, направление перемещения и деформации параметра в процессе эволюции, и дивергентную 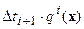 ,
,
контролирующую внешний приток – баланс количества вещества 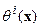 , включаемый на следующем шаге в его сдвигово-деформационную трансформацию.
, включаемый на следующем шаге в его сдвигово-деформационную трансформацию.
Для момента времени 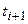 :
:
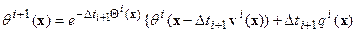 . . | (6.14) |
Член 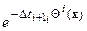 имеет смысл уплотнения (разуплотнения) происходящего за счет объемного расширения – сжатия. Описанная выше ситуация некоммутируемости операторов
имеет смысл уплотнения (разуплотнения) происходящего за счет объемного расширения – сжатия. Описанная выше ситуация некоммутируемости операторов 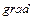 и умножения на весовую функцию
и умножения на весовую функцию 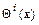 , приобретает вполне конкретный физический смысл. Различие состоит в том, происходит ли перемещение с последующим уплотнением, что соответствует соотношению (14), либо происходит перемещение уже уплотненных пород, что соответствует другой записи:
, приобретает вполне конкретный физический смысл. Различие состоит в том, происходит ли перемещение с последующим уплотнением, что соответствует соотношению (14), либо происходит перемещение уже уплотненных пород, что соответствует другой записи:
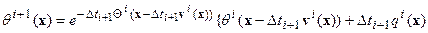 | (6.14а) |
Однако механизм уплотнения может возникать не только как следствие перемещений в рассматриваемой модели течения, а также в результате приложения внешних сил, выходящих за рамки введенной модели. Этим оправдано рассмотрение дилатационной функции Θ(x), определяющей деформации сжатия – растяжения, вне зависимости от скоростей течения, что снимает вопрос о коммутируемости сдвигов и сжатий.
Таким образом, в соответствии с (14, 14 а) процесс эволюции начальной модели 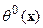 является пошаговым переходом от
является пошаговым переходом от 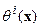 к
к 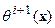 , включает в себя три вида трансформаций. Это, во-первых, дилатационные преобразования, состоящие в сжатии, либо растяжении, текущей модели на величину
, включает в себя три вида трансформаций. Это, во-первых, дилатационные преобразования, состоящие в сжатии, либо растяжении, текущей модели на величину 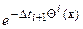 . Этот вид преобразований обозначим
. Этот вид преобразований обозначим 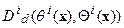 . Во-вторых, преобразование сдвигана вектор
. Во-вторых, преобразование сдвигана вектор 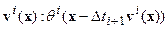 , которое обозначим
, которое обозначим 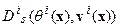 и, наконец, дивергентное преобразование, состоящее в добавлении к
и, наконец, дивергентное преобразование, состоящее в добавлении к 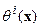 аддитивной компоненты
аддитивной компоненты 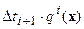 , контролирующей баланс вещества
, контролирующей баланс вещества 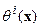 . Эту, последнюю операцию, обозначим
. Эту, последнюю операцию, обозначим 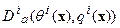 . Любой процесс движения вещества, в рамках определенной модели, распадается на последовательность из трех приведенных преобразований, осуществляемых в той, либо иной, последовательности. Результат зависит от того, какая последовательность выбрана. Это легко понять. Сдвиг, с последующим сжатием и добавлением вещества, это совсем не то же самое, что сжатие вместе с добавленным веществом и последующим сдвигом.
. Любой процесс движения вещества, в рамках определенной модели, распадается на последовательность из трех приведенных преобразований, осуществляемых в той, либо иной, последовательности. Результат зависит от того, какая последовательность выбрана. Это легко понять. Сдвиг, с последующим сжатием и добавлением вещества, это совсем не то же самое, что сжатие вместе с добавленным веществом и последующим сдвигом.
Воспользуемся теперь условием (3). Его аналог в итерационном процессе (14) записывается следующим образом:
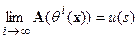 | (6.15) |
Для того чтобы обеспечить это требование, необходимо управляющие процессом эволюции (14) геодинамические параметры – скорости течений 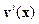 и величина внешних источников
и величина внешних источников 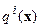 , обеспечивающих «вещественный баланс» - зависели, в том числе, и от невязки полей:
, обеспечивающих «вещественный баланс» - зависели, в том числе, и от невязки полей: 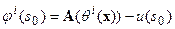 , уменьшаясь по мере ее убывания. Должно это происходить таким образом, чтобы при достижении нулевой невязки полей геодинамические параметры:
, уменьшаясь по мере ее убывания. Должно это происходить таким образом, чтобы при достижении нулевой невязки полей геодинамические параметры: 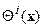 ,
, 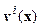 ,
, 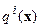 оказались равными нулю и процесс «эволюции» прекратился. Дальнейшая эволюция, если она есть, должна происходить без изменения наблюдаемого поля – т.е. в классе эквивалентности для оператора
оказались равными нулю и процесс «эволюции» прекратился. Дальнейшая эволюция, если она есть, должна происходить без изменения наблюдаемого поля – т.е. в классе эквивалентности для оператора 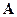 . Это будет выполнено, например, в том случае, если рассматривать величины
. Это будет выполнено, например, в том случае, если рассматривать величины 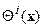 ,
, 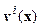 ,
, 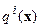 как значения линейных операторов, например, операторов типа свертки, определенных на компонентах невязки, ответственных за трансформации дилатации, сдвига и баланса соответственно. Точнее говоря, если
как значения линейных операторов, например, операторов типа свертки, определенных на компонентах невязки, ответственных за трансформации дилатации, сдвига и баланса соответственно. Точнее говоря, если 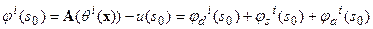 где
где 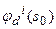 - компонента невязки, которую следует компенсировать дилатационным преобразованием,
- компонента невязки, которую следует компенсировать дилатационным преобразованием, 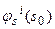 - компонента невязки, которую следует компенсировать преобразованием сдвига, а
- компонента невязки, которую следует компенсировать преобразованием сдвига, а 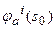 - компонента невязки, которую следует компенсировать добавлением некоторого количества вещества, то
- компонента невязки, которую следует компенсировать добавлением некоторого количества вещества, то 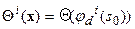 ;
; 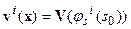 ;
; 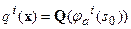 . Эти операторы могут быть определены как свертки заданных функций, характеризующих пространственное распределение дилатаций, скоростей сдвигов и осадконакопления с соответствующими компонентами невязки. Эти вопросы относятся к методическим приемам и лежат вне существа общепредметного рассмотрения.
. Эти операторы могут быть определены как свертки заданных функций, характеризующих пространственное распределение дилатаций, скоростей сдвигов и осадконакопления с соответствующими компонентами невязки. Эти вопросы относятся к методическим приемам и лежат вне существа общепредметного рассмотрения.
Теперь процесс эволюции (14) с учетом требования (15) может быть смоделирован следующим образом:
Текущее состояние модели 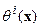 подвергается последовательности трансформаций так, как это изображено на рис.5:
подвергается последовательности трансформаций так, как это изображено на рис.5:
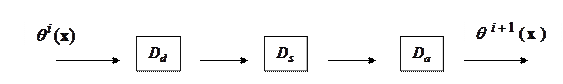
Рис.6.5. Последовательность преобразований модели.
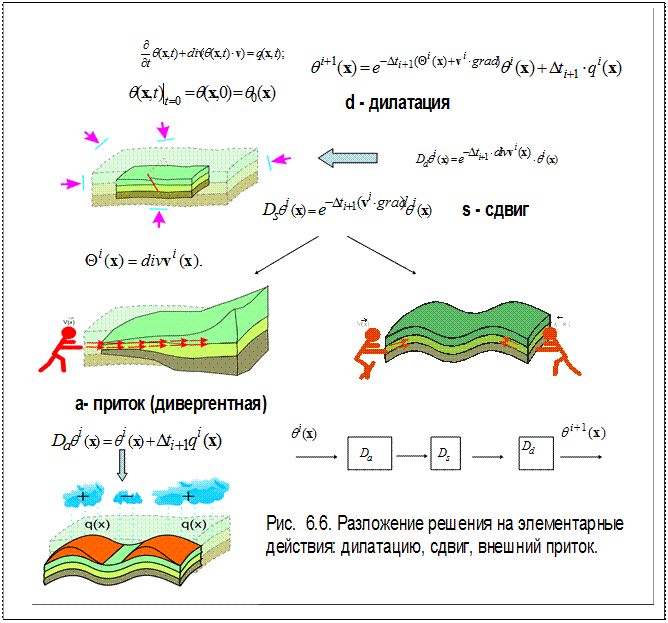 дилатационной; сдвиговой и аддитивной – внешнему притоку или оттоку вещества, который называют также дивергентной компонентной. Смысл этих движений иллюстрируется рис. 6.
дилатационной; сдвиговой и аддитивной – внешнему притоку или оттоку вещества, который называют также дивергентной компонентной. Смысл этих движений иллюстрируется рис. 6.
Последовательность их применения задается априорно, исходя из общих представлений о моделируемом развитии объекта. Например, комбинированное применение последовательности выше изображенных преобразований, записывается:
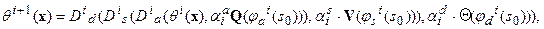 | (6.16) |
Здесь 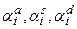 - параметры релаксации, ответственные за уменьшение соответствующих компонент
- параметры релаксации, ответственные за уменьшение соответствующих компонент 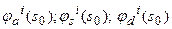 , суммарной невязки
, суммарной невязки 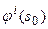 и сходимости процесса (16). Каждая из последовательности трансформаций может итерироваться самостоятельно до полной компенсации соответствующей компоненты невязки поля, либо могут применяться промежуточные формы, что продиктовано особенностями решаемой задачи.
и сходимости процесса (16). Каждая из последовательности трансформаций может итерироваться самостоятельно до полной компенсации соответствующей компоненты невязки поля, либо могут применяться промежуточные формы, что продиктовано особенностями решаемой задачи.
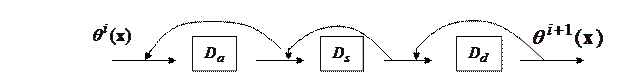
Для выбора значений параметров релаксации 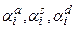 , обеспечивающих сходимость процесса (16) следует воспользоваться принципом минимальных невязок, рассмотренным в гл.2. Его вычислительные реализации могут быть различны и зависят от конкретных особенностей задачи. В постановочном плане эти параметры должны быть выбраны так, чтобы величина невязки
, обеспечивающих сходимость процесса (16) следует воспользоваться принципом минимальных невязок, рассмотренным в гл.2. Его вычислительные реализации могут быть различны и зависят от конкретных особенностей задачи. В постановочном плане эти параметры должны быть выбраны так, чтобы величина невязки 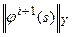 , как функция параметров
, как функция параметров 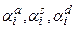 , монотонно убывала с увеличением номера
, монотонно убывала с увеличением номера 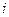 . Это означает, что для:
. Это означает, что для:
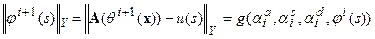 ,
,
следует на каждом шаге итерационного процесса (16) решить задачу минимизации:
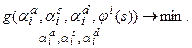 | (6.17) |
6.3. Динамика структурных моделей.
Повторение приведенных выше рассмотрений для использования эволюционно-динамических принципов при анализе структурных моделей, описываемых соотношением (6):
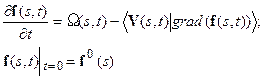
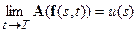 ,
,
не представляет каких-либо существенных затруднений. Однако небольшие особенности задачи требуют привести их в целях полноты рассмотрений.
Разобьем так же, как и выше, весь временной промежуток 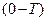 на достаточно малые интервалы времени
на достаточно малые интервалы времени 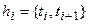
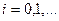 , в пределах каждого из которых можно считать
, в пределах каждого из которых можно считать 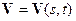 и
и 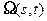 стационарными. Напомним, что:
стационарными. Напомним, что:
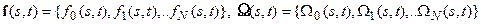 .
.
Обозначим 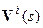 и
и 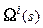 значения
значения 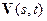 и
и 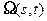 на соответствующих временных интервалах
на соответствующих временных интервалах 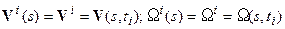 . Для каждого из интервалов
. Для каждого из интервалов 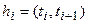 выпишем задачу движения:
выпишем задачу движения:
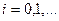 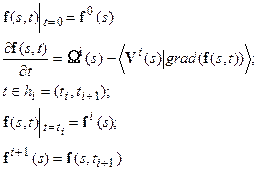 | (6.18) |
При 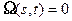 , ее решение имеет вид:
, ее решение имеет вид:
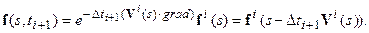
Или в покомпонентной записи:
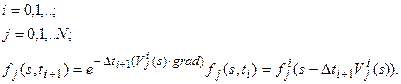
Его справедливость проверяется непосредственным дифференцированием и, в целом, это решение повторяет выписанное ранее соотношение (10) для задачи (9). Действительно:
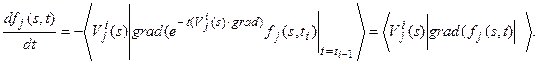
Легко понять, что решение задачи (18) с ненулевым членом 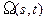 , так же, как и выше, для случая распределения параметра, можно записать в виде:
, так же, как и выше, для случая распределения параметра, можно записать в виде:
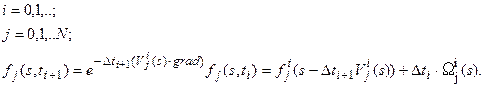 | (6.19) |
Теперь следует дополнить систему (19) требованием: 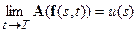 . Переходя к форме записи (19), получим:
. Переходя к форме записи (19), получим:
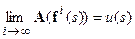 .
.
Также, как и в рассмотренном выше случае, для распределения параметра 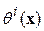 , для того, чтобы обеспечить это требование, необходимо чтобы управляющие процессом эволюции (19) геодинамические параметры – горизонтальные скорости смещения границ
, для того, чтобы обеспечить это требование, необходимо чтобы управляющие процессом эволюции (19) геодинамические параметры – горизонтальные скорости смещения границ 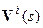 и величина эффективной вертикальной скорости смещения
и величина эффективной вертикальной скорости смещения 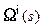 - зависели, в том числе, и от невязки полей:
- зависели, в том числе, и от невязки полей: 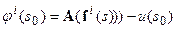 , уменьшаясь по мере ее убывания. Должно это происходить таким образом, чтобы при достижении нулевой невязки полей геодинамические параметры
, уменьшаясь по мере ее убывания. Должно это происходить таким образом, чтобы при достижении нулевой невязки полей геодинамические параметры 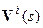 ,
, 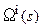 оказались равными нулю и процесс «эволюции» прекратился. Дальнейшая эволюция, если она есть, должна происходить без изменения наблюдаемого поля – т.е. в классе эквивалентности для оператора
оказались равными нулю и процесс «эволюции» прекратился. Дальнейшая эволюция, если она есть, должна происходить без изменения наблюдаемого поля – т.е. в классе эквивалентности для оператора 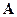 . Это будет выполнено, например, в том случае, если рассматривать величины
. Это будет выполнено, например, в том случае, если рассматривать величины 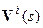 ,
, 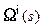 как значения линейных операторов, например, операторов типа свертки, определенных на компонентах невязки.
как значения линейных операторов, например, операторов типа свертки, определенных на компонентах невязки.
Если полная невязка поля, достигнутая на 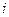 -ом шаге:
-ом шаге: 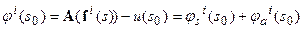 , где
, где 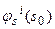 - ее компонента, которую следует компенсировать преобразованием горизонтального сдвига, а
- ее компонента, которую следует компенсировать преобразованием горизонтального сдвига, а 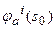 - соответственно компонента невязки, которую следует компенсировать за счет вертикального сдвига границ, то;
- соответственно компонента невязки, которую следует компенсировать за счет вертикального сдвига границ, то; 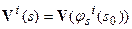 ;
; 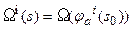 . Эти операторы могут быть определены как свертки заданных функций, характеризующих распределение горизонтальных и вертикальных скоростей сдвигов с соответствующими компонентами невязки поля.
. Эти операторы могут быть определены как свертки заданных функций, характеризующих распределение горизонтальных и вертикальных скоростей сдвигов с соответствующими компонентами невязки поля.
Далее процесс (19) переписываем с учетом этих выражений:
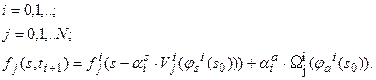 | (6.20) |
И может быть выполнен, как последовательным применением операций горизонтального и вертикального сдвигов, так и раздельным итерированием, как это было описано выше для задачи об эволюции распределения параметра.
Параметры релаксации 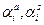 должны быть выбраны таким образом, чтобы обеспечивалась сходимость процесса (20) по невязке полей. Воспользуемся, как и ранее, принципом минимальных невязок. Величина невязки на следующем шаге должна быть меньше соответствующей величины на предыдущем. Это значит, что
должны быть выбраны таким образом, чтобы обеспечивалась сходимость процесса (20) по невязке полей. Воспользуемся, как и ранее, принципом минимальных невязок. Величина невязки на следующем шаге должна быть меньше соответствующей величины на предыдущем. Это значит, что 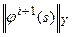 как функция параметров
как функция параметров 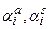 должна монотонно убывать с увеличением номера
должна монотонно убывать с увеличением номера 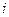 . Это влечет за собой, как и выше, что для:
. Это влечет за собой, как и выше, что для:
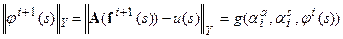 .
.
Следует на каждом шаге итерационного процесса (20) решить задачу минимизации:
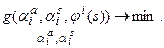 | (6.21)) |
Как итерационному процессу (20), так и (14) можно придать форму, аналогичную (5.73)[27]:
Отличие будет состоять в том, что член, аналогичный параметрам критерия оптимальности 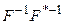 , окажется зависимым от очередного приближения
, окажется зависимым от очередного приближения 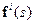 , либо
, либо 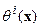 . Таким образом, метод эволюционно-динамического продолжения оказывается модификацией метода минимальных корректив с динамически меняющимся критерием оптимальности, зависящем от достигнутого состояния системы.
. Таким образом, метод эволюционно-динамического продолжения оказывается модификацией метода минимальных корректив с динамически меняющимся критерием оптимальности, зависящем от достигнутого состояния системы.
И еще одно важное замечание. Введенные геодинамические параметры, а это горизонтальные 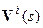 и вертикальные
и вертикальные 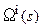 скорости[28] движений для компонент границ, деформационные
скорости[28] движений для компонент границ, деформационные 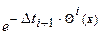 , сдвиговые
, сдвиговые 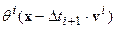 и дивергентные
и дивергентные 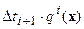 компоненты трансформаций для распределения параметра
компоненты трансформаций для распределения параметра 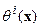 , выражены через соответствующие компоненты невязки полей. Однако само разделение на компоненты суммарной невязки носит субъективный характер и определяется спецификой рассматриваемой задачи. Но гораздо более сложным вопросом является вопрос о виде операторов, выражающих эти параметры через компоненты невязки. Предполагая эти операторы линейными и ограниченными, приходим к выводу об их интегральной форме. Например:
, выражены через соответствующие компоненты невязки полей. Однако само разделение на компоненты суммарной невязки носит субъективный характер и определяется спецификой рассматриваемой задачи. Но гораздо более сложным вопросом является вопрос о виде операторов, выражающих эти параметры через компоненты невязки. Предполагая эти операторы линейными и ограниченными, приходим к выводу об их интегральной форме. Например:
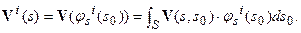
В частности: 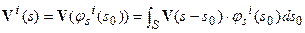 ,
,
где 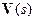 - заданная оценка горизонтальной скорости смещения границ за единицу времени. Для предметного задания этих функций необходимо сформировать класс (банк) моделей движения, характерных для изучаемого региона и отнесенных к различным элементам системы границ. То же самое относится к вертикальным или дивергентным компонентам движения и деформационным, дилатационно-сдвиговым членам для моделей эволюции параметра.
- заданная оценка горизонтальной скорости смещения границ за единицу времени. Для предметного задания этих функций необходимо сформировать класс (банк) моделей движения, характерных для изучаемого региона и отнесенных к различным элементам системы границ. То же самое относится к вертикальным или дивергентным компонентам движения и деформационным, дилатационно-сдвиговым членам для моделей эволюции параметра.
Литература.
1. Д.Хенри/Геометрическая теория полулинейных параболических уравнений. - М.: Мир, 1985.-376 с.
2. Э.Хилле, Р.Филлипс/Функциональный анализ и полугруппы. - М.:Из-во ин. лит., 1962.- 829 с.
