III. Список практических вопросов к экзамену

Высшая математика I семестр

I. Учебный план занятий

1.	10.09	Матрицы
2.	11.09	Матрицы
3.	17.09	Определители.
4.	24.09	Обратная матрица.
5.	1.10	Решение СЛУ.
6.	8.10	Решение СЛУ. Подготовка к к.р.№1.
7.	15.10	Контрольная работа №1.
8.	22.10	Глава 1. ВВЕДЕНИЕ В АНАЛИЗ
9.	29.10	Глава 2. ПРОИЗВОДНАЯ ФУНКЦИИ
10.	5.11	Глава 2. ПРОИЗВОДНАЯ ФУНКЦИИ
11.	12.11	Глава 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
12.	19.11	Глава 4. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
13.	26.11	Подготовка к к.р.№2-3.
14.	3.12	Контрольная работа №2
15.	10.12	Контрольная работа №3 ( домашняя - принимаю)
16.	17.12	Анализ итогов и ошибок по К.р. №2
17.	24.12	Анализ итогов и ошибок по К.р. №3

II. ТЕКУЩИЙ КООНТРОЛЬ

Контрольная работа №1

	Линейная алгебра 28 (+-6)
	В-т
балл

Контрольная работа №2

Матанализ 54 (+-11)
В-т	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.	16.

Контрольная работа №3

Исследование функции 18(+-4)
В-т	1.	2.	3.	4.	5.	6.	7.	8.

Таблица корректировки баллов в зависимости от сложности варианта:

	1-10 вариант	11-40 вариант	41-50 вариант
Линейная алгебра	-6 баллов	Не изменяются	+6 баллов
Матанализ.	-12 баллов	Не изменяются	+12 баллов
Исследование функции	-4 баллов	Не изменяются	+4 баллов

Таблица корректировки баллов за все остальное:

За нахождение ошибок в учебных пособиях	индивидуальные задания	.
За каждую ошибку от 1-5 баллов. Ошибки на запятые, двоеточия и т.п. не принимаются.	За индивидуальные задания по практике и решебникам оценю индивидуально каждого

Таблица перевода текущих баллов в экзаменационную оценку:

0-30	31-55	56-80	Свыше 81
неудовлетворительно	удовлетворительно	хорошо	отлично

III. ЭКЗАМЕН ЗА I СЕМЕСТР ПО МАТЕМАТИКЕ

I. Расписание экзаменов и консультаций (будет уточняться)

число	День недели	Аудитория /время	предмет	Вид занятия
21.01	четверг	13.15	УТОЧНЮ!!	математика	Консул. +принимаю ДОЛГИ
22.01	Пятница	9.00	УТОЧНЮ!!	математика	Экзамен

II. Список теоретических вопросов к экзамену

	ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
1.	Основные понятия
2.	Действия над матрицами.
3.	Основные понятия
4.	Основные свойства определителей
5.	Обратная матрица
6.	Основные понятия
7.	Решение невырожденных линейных систем. Метод обратной матрицы. Метод Крамера
8.	Решение систем линейных уравнений методом Гаусса
9.	Решение систем линейных уравнений методом полного исключения неизвестных (метод Жордана-Гаусса.)
	ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
10.	Основные сведения о функциях
11.	Понятие функции (отображения). График функции. Способы задания. Основные свойства.
12.	Сложная функция. Обратная функция
13.	Основные элементарные функции : линейная функция.
14.	Основные элементарные функции : квадратичная функция
15.	Основные элементарные функции : степенная функция.
16.	Основные элементарные функции : дробно-рациональная функция.
17.	Основные элементарные функции : модуль.
18.	Основные элементарные функции : иррациональная функция.
19.	Основные элементарные функции : логарифмическая функция.
20.	Основные элементарные функции : показательная функция.
21.	Основные элементарные функции: тригонометрические функции
22.	Основные элементарные функции: обратные тригонометрические функции.
23.	Числовые последовательности и их свойства
24.	Предел последовательности. Операции над числовыми последовательностями.
25.	Ограниченные и неограниченные последовательности. Бесконечно малые и бесконечно большие последовательности.
26.	Сходимость числовых последовательностей. Основные свойства сходящихся последовательностей. монотонные последовательности. Теорема Вейерштрасса
27.	Односторонние пределы. Понятие предела функции в точке.
28.	Предел функции при .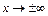
29.	Свойства пределов.
30.	Бесконечно малые и бесконечно большие функции.
31.	Первый и второй замечательные пределы.
32.	Техника вычисления пределов числовых последовательностей
33.	Предел функции
34.	Техника вычисления пределов функций
35.	Непрерывность функции
36.	Понятие производной, её геометрический и механический смысл. Связь между непрерывностью и дифференцируемостью функции
37.	Техника дифференцирования
38.	Основные теоремы дифференциального исчисления
39.	Правило Лопиталя
40.	Понятие дифференциала функции, его геометрический смысл
41.	Техника вычисления дифференциалов
42.	Применение дифференциалов к приближенным вычислениям
43.	Исследование по первой производной: возрастание и убывание функции. Максимум и минимум функции. Наибольшее и наименьшее значение функции
44.	Исследование по второй производной: выпуклость графика функции. Точки перегиба.
45.	Асимптоты графика функции
46.	Общая схема исследования функции и построения графика